CHAPTER 11
EXAMPLES: MISSING DATA MODELING AND BAYESIAN ANALYSIS
Mplus provides estimation of models with missing data using both frequentist and Bayesian analysis. Descriptive statistics and graphics are available for understanding dropout in longitudinal studies. Bayesian analysis provides multiple imputation for missing data as well as plausible values for latent variables.
With frequentist analysis, Mplus provides maximum likelihood estimation under MCAR (missing completely at random), MAR (missing at random), and NMAR (not missing at random) for continuous, censored, binary, ordered categorical (ordinal), unordered categorical (nominal), counts, or combinations of these variable types (Little & Rubin, 2002). MAR means that missingness can be a function of observed covariates and observed outcomes. For censored and categorical outcomes using weighted least squares estimation, missingness is allowed to be a function of the observed covariates but not the observed outcomes. When there are no covariates in the model, this is analogous to pairwise present analysis. Non-ignorable missing data (NMAR) modeling is possible using maximum likelihood estimation where categorical outcomes are indicators of missingness and where missingness can be predicted by continuous and categorical latent variables (Muthén, Jo, & Brown, 2003; Muthén et al., 2011). This includes selection models, pattern-mixture models, and shared-parameter models (see, e.g., Muthén et al., 2011). In all models, observations with missing data on covariates are deleted because models are estimated conditional on the covariates. Covariate missingness can be modeled if the covariates are brought into the model and distributional assumptions such as normality are made about them. With missing data, the standard errors for the parameter estimates are computed using the observed information matrix (Kenward & Molenberghs, 1998). Bootstrap standard errors and confidence intervals are also available with missing data.
With Bayesian analysis, modeling with missing data gives asymptotically the same results as maximum-likelihood estimation under MAR. Multiple imputation of missing data using Bayesian analysis (Rubin, 1987; Schafer, 1997) is also available. For an overview, see Enders (2010). Both unrestricted H1 models and restricted H0 models can be used for imputation. Several different algorithms are available for H1 imputation, including sequential regression, also referred to as chained regression, in line with Raghunathan et al. (2001); see also van Buuren (2007). Multiple imputation of plausible values for latent variables is provided. For applications of plausible values in the context of Item Response Theory, see Mislevy et al. (1992) and von Davier et al. (2009). Multiple data sets generated using multiple imputation can be analyzed with frequentist estimators using a special feature of Mplus. Parameter estimates are averaged over the set of analyses, and standard errors are computed using the average of the standard errors over the set of analyses and the between analysis parameter estimate variation (Rubin, 1987; Schafer, 1997). A chi-square test of overall model fit is provided with maximum-likelihood estimation (Asparouhov & Muthén, 2008c; Enders, 2010).
Following is the set of frequentist examples included in this chapter:
· 11.1: Growth model with missing data using a missing data correlate
· 11.2: Descriptive statistics and graphics related to dropout in a longitudinal study
· 11.3: Modeling with data not missing at random (NMAR) using the Diggle-Kenward selection model*
· 11.4: Modeling with data not missing at random (NMAR) using a pattern-mixture model
Following is the set of Bayesian examples included in this chapter:
· 11.5: Multiple imputation for a set of variables with missing values
· 11.6: Multiple imputation followed by the estimation of a growth model using maximum likelihood
· 11.7: Multiple imputation of plausible values using Bayesian estimation of a growth model
· 11.8: Multiple imputation using a two-level factor model with categorical outcomes followed by the estimation of a growth model
* Example uses numerical integration in the estimation of the model. This can be computationally demanding depending on the size of the problem.
TITLE: this is an example of a linear growth model with missing data on a continuous outcome using a missing data correlate to improve the plausibility of MAR
DATA: FILE = ex11.1.dat;
VARIABLE: NAMES = x1 x2 y1-y4 z;
USEVARIABLES = y1-y4;
MISSING = ALL (999);
AUXILIARY = (m) z;
ANALYSIS: ESTIMATOR = ML;
MODEL: i s | y1@0 y2@1 y3@2 y4@3;
OUTPUT: TECH1;
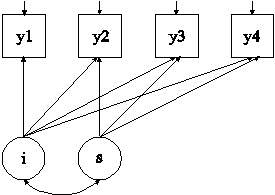
In this example, the linear growth model at four time points with missing data on a continuous outcome shown in the picture above is estimated using a missing data correlate. The missing data correlate is not part of the growth model but is used to improve the plausibility of the MAR assumption of maximum likelihood estimation (Collins, Schafer, & Kam, 2001; Graham, 2003; Enders, 2010). The missing data correlate is allowed to correlate with the outcome while providing the correct number of parameters and chi-square test for the analysis model as described in Asparouhov and Muthén (2008b).
TITLE: this is an example of a linear growth model with missing data on a continuous outcome using a missing data correlate to improve the plausibility of MAR
The TITLE command is used to provide a title for the analysis. The title is printed in the output just before the Summary of Analysis.
DATA: FILE = ex11.1.dat;
The DATA command is used to provide information about the data set to be analyzed. The FILE option is used to specify the name of the file that contains the data to be analyzed, ex11.1.dat. Because the data set is in free format, the default, a FORMAT statement is not required.
VARIABLE: NAMES = x1 x2 y1-y4 z;
USEVARIABLES = y1-y4;
MISSING = ALL (999);
AUXILIARY = (m) z;
The VARIABLE command is used to provide information about the variables in the data set to be analyzed. The NAMES option is used to assign names to the variables in the data set. The data set in this example contains seven variables: x1, x2, y1, y2, y3, y4, and z. Note that the hyphen can be used as a convenience feature in order to generate a list of names. If not all of the variables in the data set are used in the analysis, the USEVARIABLES option can be used to select a subset of variables for analysis. Here the variables y1, y2, y3, and y4 have been selected for analysis. They represent the outcome measured at four equidistant occasions. The MISSING option is used to identify the values or symbol in the analysis data set that are treated as missing or invalid. The keyword ALL specifies that all variables in the analysis data set have the missing value flag of 999. The AUXILIARY option using the m setting is used to identify a set of variables that will be used as missing data correlates in addition to the analysis variables. In this example, the variable z is a missing data correlate.
ANALYSIS: ESTIMATOR = ML;
The ANALYSIS command is used to describe the technical details of the analysis. The ESTIMATOR option is used to specify the estimator to be used in the analysis. By specifying ML, maximum likelihood estimation is used.
MODEL: i s | y1@0 y2@1 y3@2 y4@3;
The MODEL command is used to describe the model to be estimated. The | symbol is used to name and define the intercept and slope factors in a growth model. The names i and s on the left-hand side of the | symbol are the names of the intercept and slope growth factors, respectively. The statement on the right-hand side of the | symbol specifies the outcome and the time scores for the growth model. The time scores for the slope growth factor are fixed at 0, 1, 2, and 3 to define a linear growth model with equidistant time points. The zero time score for the slope growth factor at time point one defines the intercept growth factor as an initial status factor. The coefficients of the intercept growth factor are fixed at one as part of the growth model parameterization. The residual variances of the outcome variables are estimated and allowed to be different across time and the residuals are not correlated as the default.
In the parameterization of the growth model shown here, the intercepts of the outcome variables at the four time points are fixed at zero as the default. The means and variances of the growth factors are estimated as the default, and the growth factor covariance is estimated as the default because the growth factors are independent (exogenous) variables. The default estimator for this type of analysis is maximum likelihood. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator.
OUTPUT: TECH1;
The OUTPUT command is used to request additional output not included as the default. The TECH1 option is used to request the arrays containing parameter specifications and starting values for all free parameters in the model.
TITLE: this is an example of descriptive statistics and graphics related to dropout in a longitudinal study
DATA: FILE = ex11.2.dat;
VARIABLE: NAMES = z1-z5 y0 y1-y5;
USEVARIABLES = z1-z5 y0-y5 d1-d5;
MISSING = ALL (999);
DATA MISSING:
NAMES = y0-y5;
TYPE = DDROPOUT;
BINARY = d1-d5;
DESCRIPTIVE = y0-y5 | * z1-z5;
ANALYSIS: TYPE = BASIC;
PLOT: TYPE = PLOT2;
SERIES = y0-y5(*);
In this example, descriptive statistics and graphics related to dropout in a longitudinal study are obtained. The descriptive statistics show the mean and standard deviation for sets of variables related to the outcome for those who drop out or not before the next time point. These means are plotted to help in understanding dropout.
The DATA MISSING command is used to create a set of binary variables that are indicators of missing data or dropout for another set of variables. Dropout indicators can be scored as discrete-time survival indicators or dummy dropout indicators. The NAMES option identifies the set of variables that are used to create a set of binary variables that are indicators of missing data. In this example, they are y0, y1, y2, y3, y4, and y5. These variables must be variables from the NAMES statement of the VARIABLE command. The TYPE option is used to specify how missingness is coded. In this example, the DDROPOUT setting specifies that binary dummy dropout indicators will be used. The BINARY option is used to assign the names d1, d2, d3, d4, and d5 to the new set of binary variables. There is one less dummy dropout indicator than there are time points. The DESCRIPTIVE option is used in conjunction with TYPE=BASIC of the ANALYSIS command and the DDROPOUT setting to specify the sets of variables for which additional descriptive statistics are computed. For each variable, the mean and standard deviation are computed using all observations without missing on the variable and for those who drop out or not before the next time point.
The PLOT command is used to request graphical displays of observed data and analysis results. These graphical displays can be viewed after the analysis is completed using a post-processing graphics module. The TYPE option is used to specify the types of plots that are requested. The setting PLOT2 is used to obtain missing data plots of dropout means and sample means. The SERIES option is used to list the names of the set of variables to be used in plots where the values are connected by a line. The asterisk (*) in parentheses following the variable names indicates that the values 1, 2, 3, 4, 5, and 6 will be used on the x-axis. An explanation of the other commands can be found in Example 11.1.
TITLE: this is an example of modeling with data not missing at random (NMAR) using the Diggle-Kenward selection model
DATA: FILE = ex11.3.dat;
VARIABLE: NAMES = z1-z5 y0 y1-y5;
USEVARIABLES = y0-y5 d1-d5;
MISSING = ALL (999);
CATEGORICAL = d1-d5;
DATA MISSING:
NAMES = y0-y5;
TYPE = SDROPOUT;
BINARY = d1-d5;
ANALYSIS: ESTIMATOR = ML;
ALGORITHM = INTEGRATION;
INTEGRATION = MONTECARLO;
PROCESSORS = 2;
MODEL: i s | y0@0 y1@1 y2@2 y3@3 y4@4 y5@5;
d1 ON y0 (1)
y1 (2);
d2 ON y1 (1)
y2 (2);
d3 ON y2 (1)
y3 (2);
d4 ON y3 (1)
y4 (2);
d5 ON y4 (1)
y5 (2);
OUTPUT: TECH1;
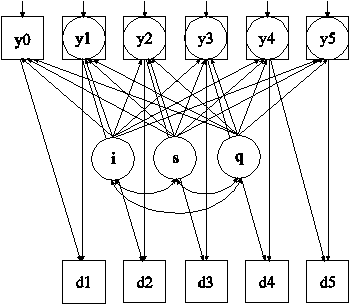
In this example, the linear growth model at six time points with missing data on a continuous outcome shown in the picture above is estimated. The data are not missing at random because dropout is related to both past and current outcomes where the current outcome is missing for those who drop out. In the picture above, y1 through y5 are shown in both circles and squares where circles imply that dropout has occurred and squares imply that dropout has not occurred. The Diggle-Kenward selection model (Diggle & Kenward, 1994) is used to jointly estimate a growth model for the outcome and a discrete-time survival model for the dropout indicators (see also Muthén et al, 2011).
In this example, the SDROPOUT setting of the TYPE option specifies that binary discrete-time (event-history) survival dropout indicators will be used. In the ANALYSIS command, ALGORITHM=INTEGRATION is required because latent continuous variables corresponding to missing data on the outcome influence the binary dropout indicators. INTEGRATION=MONTECARLO is required because the dimensions of integration vary across observations. In the MODEL command, the ON statements specify the logistic regressions of a dropout indicator at a given time point regressed on the outcome at the previous time point and the outcome at the current time point. The outcome at the current time point is latent, missing, for those who have dropped out since the last time point. The logistic regression coefficients are held equal across time. An explanation of the other commands can be found in Examples 11.1 and 11.2.
TITLE: this is an example of modeling with data not missing at random (NMAR) using a pattern-mixture model
DATA: FILE = ex11.4.dat;
VARIABLE: NAMES = z1-z5 y0 y1-y5;
USEVARIABLES = y0-y5 d1-d5;
MISSING = ALL (999);
DATA MISSING:
NAMES = y0-y5;
TYPE = DDROPOUT;
BINARY = d1-d5;
MODEL: i s | y0@0 y1@1 y2@2 y3@3 y4@4 y5@5;
i ON d1-d5;
s ON d3-d5;
s ON d1 (1);
s ON d2 (1);
OUTPUT: TECH1;
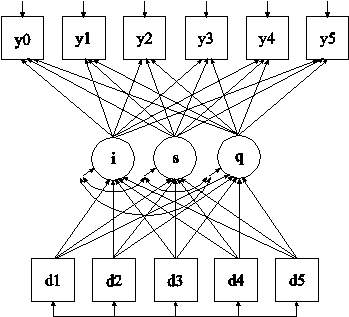
In this example, the linear growth model at six time points with missing data on a continuous outcome shown in the picture above is estimated. The data are not missing at random because dropout is related to both past and current outcomes where the current outcome is missing for those who drop out. A pattern-mixture model (Little, 1995; Hedeker & Gibbons, 1997; Demirtas & Schafer, 2003) is used to estimate a growth model for the outcome with binary dummy dropout indicators used as covariates (see also Muthén et al, 2011).
The MODEL command is used to specify that the dropout indicators influence the growth factors. The ON statements specify the linear regressions of the intercept and slope growth factors on the dropout indicators. The coefficient in the linear regression of s on d1 is not identified because the outcome is observed only at the first time point for the dropout pattern with d1 equal to one. This regression coefficient is held equal to the linear regression of s on d2 for identification purposes. An explanation of the other commands can be found in Examples 11.1 and 11.2.
TITLE: this is an example of multiple imputation
for a set of variables with missing values
DATA: FILE = ex11.5.dat;
VARIABLE: NAMES = x1 x2 y1-y4 v1-v50 z1-z5;
USEVARIABLES = x1 x2 y1-y4 z1-z5;
AUXILIARY = v1-v10;
MISSING = ALL (999);
DATA IMPUTATION:
IMPUTE = y1-y4 x1 (c) x2;
NDATASETS = 10;
SAVE = missimp*.dat;
ANALYSIS: TYPE = BASIC;
OUTPUT: TECH8;
In this example, multiple imputation for a set of variables with missing values is carried out using Bayesian analysis (Rubin, 1987; Schafer, 1997). The NAMES option is used to assign names to the variables in the original data set. The variables on the USEVARIABLES list are used to create the imputed data sets. The AUXILIARY option is used to specify the variables that are not used in the data imputation but that will be saved with the imputed data sets. In the DATA IMPUTATION command, the IMPUTE option is used to specify the variables for which missing values will be imputed. A c in parentheses following a variable indicates that it is categorical. The NDATASETS option is used to specify the number of imputed data sets to create. In this example, ten imputed data sets will be created. The SAVE option is used to save the imputed data sets for further analysis using TYPE=IMPUTATION in the DATA command. All variables on the USEVARIABLES and AUXILIARY lists are saved. The asterisk in the data set name is replaced by the number of the imputation. The data sets saved are missimp1.dat, missimp2.dat, etc. The imputed data sets will contain the variables x1, x2, y1-y4, z1-z5, and v1-v10 in that order. The data sets can be used in a subsequent analysis using TYPE=IMPUTATION in the DATA command. See Example 13.13. An explanation of the other commands can be found in Example 11.1.
EXAMPLE 11.6: MULTIPLE IMPUTATION FOLLOWED BY THE ESTIMATION OF A GROWTH MODEL USING MAXIMUM LIKELIHOOD
TITLE: this is an example of multiple imputation followed by the estimation of a growth model using maximum likelihood
DATA: FILE = ex11.6.dat;
VARIABLE: NAMES = x1 y1-y4 z x2;
USEVARIABLES = y1-y4 x1 x2;
MISSING = ALL(999);
DATA IMPUTATION:
IMPUTE = y1-y4 x1 (c) x2;
NDATASETS = 10;
ANALYSIS: ESTIMATOR = ML;
MODEL: i s | y1@0 y2@1 y3@2 y4@3;
i s ON x1 x2;
OUTPUT: TECH1 TECH8;
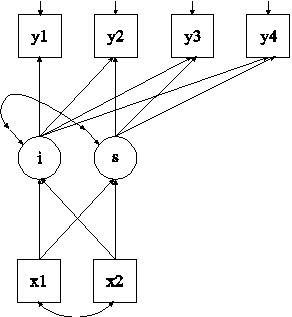
In this example, multiple imputation for a set of variables with missing values is carried out using Bayesian analysis (Rubin, 1987; Schafer, 1997). The imputed data sets are used in the estimation of the growth model shown in the picture above using maximum likelihood estimation.
The DATA IMPUTATION command is used when a data set contains missing values to create a set of imputed data sets using multiple imputation methodology. Multiple imputation is carried out using Bayesian estimation. Data are imputed using an unrestricted H1 model. The IMPUTE option is used to specify the analysis variables for which missing values will be imputed. In this example, missing values will be imputed for y1, y2, y3, y4, x1, and x2. The c in parentheses after x1 specifies that x1 is treated as a categorical variable for data imputation. The NDATASETS option is used to specify the number of imputed data sets to create. The default is five. In this example, 10 data sets will be imputed.
The maximum likelihood parameter estimates for the growth model are averaged over the set of 10 analyses and standard errors are computed using the average of the standard errors over the set of 10 analyses and the between analysis parameter estimate variation (Rubin, 1987; Schafer, 1997). A chi-square test of overall model fit is provided (Asparouhov & Muthén, 2008c; Enders, 2010). The ESTIMATOR option is used to specify the estimator to be used in the analysis. By specifying ML, maximum likelihood estimation is used. An explanation of the other commands can be found in Examples 11.1 and 11.5.
TITLE: this is an example of multiple imputation of plausible values generated from a multiple indicator linear growth model for categorical outcomes using Bayesian estimation
DATA: FILE = ex11.7.dat;
VARIABLE: NAMES = u11 u21 u31 u12 u22 u32 u13 u23 u33;
CATEGORICAL = u11-u33;
ANALYSIS: ESTIMATOR = BAYES;
PROCESSORS = 2;
MODEL: f1 BY u11
u21-u31 (1-2);
f2 BY u12
u22-u32 (1-2);
f3 BY u13
u23-u33 (1-2);
[u11$1 u12$1 u13$1] (3);
[u21$1 u22$1 u23$1] (4);
[u31$1 u32$1 u33$1] (5);
i s | f1@0 f2@1 f3@2;
DATA IMPUTATION:
NDATASETS = 20;
SAVE = ex11.7imp*.dat;
SAVEDATA: FILE = ex11.7plaus.dat;
SAVE = FSCORES (20);
FACTORS = f1-f3 i s;
SAVE = LRESPONSES (20);
LRESPONSES = u11-u33;
OUTPUT: TECH1 TECH8;
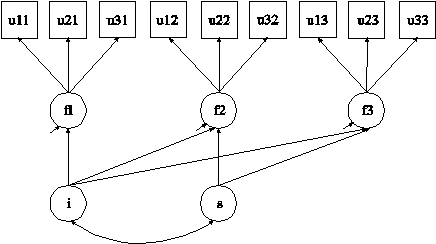
In this example, plausible values (Mislevy et al., 1992; von Davier et al., 2009) are obtained by multiple imputation (Rubin, 1987; Schafer,
1997) based on a multiple indicator linear growth model for categorical outcomes
shown in the picture above using Bayesian estimation. The
plausible values in the multiple imputation data sets can be used for
subsequent analysis.
The ANALYSIS command is used to describe the technical details of the analysis. The ESTIMATOR option is used to specify the estimator to be used in the analysis. By specifying BAYES, Bayesian estimation is used to estimate the model. The DATA IMPUTATION command is used when a data set contains missing values to create a set of imputed data sets using multiple imputation methodology. Multiple imputation is carried out using Bayesian estimation. When a MODEL command is used with ESTIMATOR=BAYES, data are imputed using the H0 model specified in the MODEL command. The IMPUTE option is used to specify the analysis variables for which missing values will be imputed. When the IMPUTE option is not used, no imputation of missing data for the analysis variables is done.
In the DATA IMPUTATION command, the NDATASETS option is used to specify the number of imputed data sets to create. The default is five. In this example, 20 data sets will be imputed to more fully represent the variability in the latent variables. The SAVE option is used to save the imputed data sets for subsequent analysis. The asterisk (*) is replaced by the number of the imputed data set. A file is also produced that contains the names of all of the data sets. To name this file, the asterisk (*) is replaced by the word list. In this example, the file is called ex11.7implist.dat. The multiple imputation data sets named using the SAVE option contain the imputed values for each observation for the observed variables u11 through u33; the continuous latent response variables u11* through u33* for the categorical outcomes u11 through u33; and the factor scores for the latent variables f1, f2, f3, i, and s.
In the SAVEDATA command, the FILE option is used to specify the name of the ASCII file in which the individual-level data used in the analysis will be saved. In this example, the file is called ex11.7plaus.dat. When SAVE=FSCORES is used with ESTIMATOR=BAYES, a distribution of factor scores, called plausible values, is obtained for each observation. The following summaries are saved along with the other analysis variables: mean, median, standard deviation, lower 2.5% limit, and upper 97.5% limit. The number 20 in parentheses is the number of imputations or draws that are used from the Bayesian posterior distribution to compute the plausible value distribution for each observation. The FACTORS option is used to specify the names of the factors for which the plausible value distributions will also be saved. In this example, the plausible value distributions will be saved for f1, f2, f3, i, and s.
When SAVE=LRESPONSES is used with ESTIMATOR=BAYES, a distribution of latent response variable scores is obtained for each observation. The following summaries are saved along with the other analysis variables: mean, median, standard deviation, lower 2.5% limit, and upper 97.5% limit. The number 20 in parentheses is the number of imputations or draws that are used from the Bayesian posterior distribution to compute the latent response variable distribution for each observation. The LRESPONSES option is used to specify the names of the latent response variables underlying categorical outcomes for which the latent response variable distributions will also be saved. In this example, the latent response variable distributions will be saved for u11 through u33. An explanation of the other commands can be found in Examples 11.1 and 11.2.
TITLE: this is an example of multiple imputation using a two-level factor model with categorical outcomes
DATA: FILE = ex11.8.dat;
VARIABLE: NAMES are u11 u21 u31 u12 u22 u32 u13 u23 u33 clus;
CATEGORICAL = u11-u33;
CLUSTER = clus;
MISSING = ALL (999);
ANALYSIS: TYPE = TWOLEVEL;
ESTIMATOR = BAYES;
PROCESSORS = 2;
MODEL: %WITHIN%
f1w BY u11
u21 (1)
u31 (2);
f2w BY u12
u22 (1)
u32 (2);
f3w BY u13
u23 (1)
u33 (2);
%BETWEEN%
fb BY u11-u33*1;
fb@1;
DATA IMPUTATION:
IMPUTE = u11-u33(c);
SAVE = ex11.8imp*.dat;
OUTPUT: TECH1 TECH8;

In this example, missing values are imputed for a set of variables using multiple imputation (Rubin, 1987; Schafer, 1997). In the first part of this example, imputation is done using the two-level factor model with categorical outcomes shown in the picture above. In the second part of this example, the multiple imputation data sets are used for a two-level multiple indicator growth model with categorical outcomes using two-level weighted least squares estimation.
The ANALYSIS command is used to describe the technical details of the analysis. The TYPE option is used to describe the type of analysis. By selecting TWOLEVEL, a multilevel model with random intercepts is estimated. The ESTIMATOR option is used to specify the estimator to be used in the analysis. By specifying BAYES, Bayesian estimation is used to estimate the model. The DATA IMPUTATION command is used when a data set contains missing values to create a set of imputed data sets using multiple imputation methodology. Multiple imputation is carried out using Bayesian estimation. When a MODEL command is used, data are imputed using the H0 model specified in the MODEL command. The IMPUTE option is used to specify the analysis variables for which missing values will be imputed. In this example, missing values will be imputed for u11, u21, u31, u12, u22, u32, u13, u23, and u33. The c in parentheses after the list of variables specifies that they are treated as categorical variables for data imputation. An explanation of the other commands can be found in Examples 11.1, 11.2, and 11.5.
TITLE: this is an example of a two-level multiple
indicator growth model with categorical outcomes using multiple imputation data
DATA: FILE = ex11.8implist.dat;
TYPE = IMPUTATION;
VARIABLE: NAMES are u11 u21 u31 u12 u22 u32 u13 u23 u33 clus;
CATEGORICAL = u11-u33;
CLUSTER = clus;
ANALYSIS: TYPE = TWOLEVEL;
ESTIMATOR = WLSMV;
PROCESSORS = 2;
MODEL: %WITHIN%
f1w BY u11
u21 (1)
u31 (2);
f2w BY u12
u22 (1)
u32 (2);
f3w BY u13
u23 (1)
u33 (2);
iw sw | f1w@0 f2w@1 f3w@2;
%BETWEEN%
f1b BY u11
u21 (1)
u31 (2);
f2b BY u12
u22 (1)
u32 (2);
f3b BY u13
u23 (1)
u33 (2);
[u11$1 u12$1 u13$1] (3);
[u21$1 u22$1 u23$1] (4);
[u31$1 u32$1 u33$1] (5);
u11-u33;
ib sb | f1b@0 f2b@1 f3b@2;
[f1b-f3b@0 ib@0 sb];
f1b-f3b (6);
OUTPUT: TECH1 TECH8;
SAVEDATA: SWMATRIX = ex11.8sw*.dat;
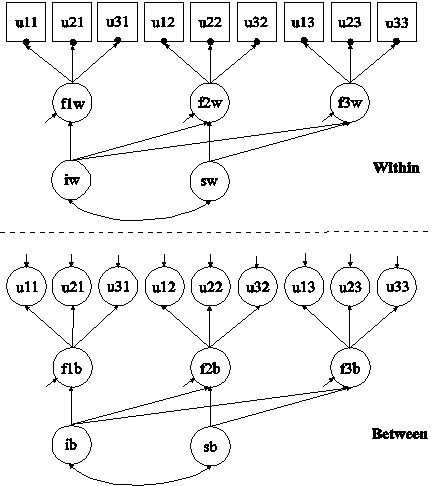
In the second part of this example, the data sets saved in the first part of the example are used in the estimation of a two-level multiple indicator growth model with categorical outcomes. The model is the same as in Example 9.15. The two-level weighted least squares estimator described in Asparouhov and Muthén (2007) is used in this example. This estimator does not handle missing data using MAR. By doing Bayesian multiple imputation as a first step, this disadvantage is avoided given that there is no missing data for the weighted least squares analysis. To save computational time in subsequent analyses, the two-level weighted least squares sample statistics and weight matrix for each of the imputed data sets are saved.
The ANALYSIS command is used to describe the technical details of the analysis. The TYPE option is used to describe the type of analysis. By selecting TWOLEVEL, a multilevel model with random intercepts is estimated. The ESTIMATOR option is used to specify the estimator to be used in the analysis. By specifying WLSMV, a robust weighted least squares estimator is used. The SAVEDATA command is used to save the analysis data, auxiliary variables, and a variety of analysis results. The SWMATRIX option is used with TYPE=TWOLEVEL and weighted least squares estimation to specify the name of the ASCII file in which the within- and between-level sample statistics and their corresponding estimated asymptotic covariance matrix will be saved. In this example, the files are called ex11.8sw*.dat where the asterisk (*) is replaced by the number of the imputed data set. A file is also produced that contains the names of all of the imputed data sets. To name this file, the asterisk (*) is replaced by the word list. The file, in this case ex11.8swlist.dat, contains the names of the imputed data sets.
To use the saved within- and between-level sample statistics and their corresponding estimated asymptotic covariance matrix for each imputation in a subsequent analysis, specify:
DATA:
FILE = ex11.8implist.dat;
TYPE = IMPUTATION;
SWMATRIX = ex11.8swlist.dat;
An explanation of the other commands can be found in Examples 9.15, 11.1, 11.2, and 11.5.