CHAPTER 14
SPECIAL MODELING ISSUES
In this chapter, the following special modeling issues are discussed:
· Model estimation
· Multiple group analysis
· Missing data
· Categorical mediating variables
· Calculating probabilities from probit regression coefficients
· Calculating probabilities from logistic regression coefficients
· Parameterization of models with more than one categorical latent variable
In the model estimation section, technical details of parameter specification and model estimation are discussed. In the multiple group analysis section, differences in model specification, differences in data between single-group analysis and multiple group analysis, and testing for measurement invariance are described. In the missing data section, estimation of models when there is missing data and special features for data missing by design are described. There is a section that describes how categorical mediating variables are treated in model estimation. There is a section on calculating probabilities for probit regression coefficients. In the section on calculating probabilities for logistic regression coefficients, a brief background with examples of converting logistic regression coefficients to probabilities and odds is given. In the section on parameterization with multiple categorical latent variables, conventions related to logistic and loglinear parameterizations of these models are described.
There are several important issues involved in model estimation beyond specifying the model. The following general analysis considerations are discussed below:
· Parameter default settings
· Parameter default starting values
· User-specified starting values for mixture models
· Multiple solutions for mixture models
· Convergence problems
· Model identification
· Numerical integration
PARAMETER DEFAULT SETTINGS
Default settings are used to simplify the model specification. In order to minimize the information provided by the user, certain parameters are free, constrained to be equal, or fixed at zero as the default. These defaults are chosen to reflect common practice and to avoid computational problems. These defaults can be overridden. Because of the extensive default settings, it is important to examine the analysis results to verify that the model that is estimated is the intended model. The output contains parameter estimates for all free parameters in the model, including those that are free by default and those that are free because of the model specification. Parameters that are fixed in the input file are also listed with these results. Parameters fixed by default are not included. In addition, the TECH1 option of the OUTPUT command shows which parameters in the model are free to be estimated and which are fixed.
Following are the default settings for means/intercepts/thresholds in the model when they are included:
· Means of observed independent variables are not part of the model. The model is estimated conditioned on the observed independent variables.
· In single group analysis, intercepts and thresholds of observed dependent variables are free.
· In multiple group analysis and multiple class analysis, intercepts and thresholds of observed dependent variables that are used as factor indicators for continuous latent variables are free and equal across groups or classes. Otherwise, they are free and unequal in the other groups or classes except for the inflation part of censored and count variables in which case they are free and equal.
· In single group analysis, means and intercepts of continuous latent variables are fixed at zero.
· In multiple group analysis and multiple class analysis, means and intercepts of continuous latent variables are fixed at zero in the first group and last class and are free and unequal in the other groups or classes except when a categorical latent variable is regressed on a continuous latent variable. In this case, the means and intercepts of continuous latent variables are fixed at zero in all classes.
· Logit means and intercepts of categorical latent variables are fixed at zero in the last class and free and unequal in the other classes.
Following are the default settings for variances/residual variances/scale factors:
· Variances of observed independent variables are not part of the model. The model is estimated conditioned on the observed independent variables.
· In single group analysis and multiple group analysis, variances and residual variances of continuous and censored observed dependent variables and continuous latent variables are free. In multiple class analysis, variances/residual variances of continuous and censored observed dependent variables and continuous latent variables are free and equal across classes.
· In single group analysis using the Delta parameterization, scale factors of latent response variables for categorical observed dependent variables are fixed at one. In multiple group analysis using the Delta parameterization, scale factors of latent response variables for categorical observed dependent variables are fixed at one in the first group and are free and unequal in the other groups.
· In single group analysis using the Theta parameterization, variances and residual variances of latent response variables for categorical observed dependent variables are fixed at one. In multiple group analysis using the Theta parameterization, variances and residual variances of latent response variables for categorical observed dependent variables are fixed at one in the first group and are free and unequal in the other groups.
Following are the default settings for covariances/residual covariances:
· Covariances among observed independent variables are not part of the model. The model is estimated conditioned on the observed independent variables.
· In single group analysis and multiple group analysis, covariances among continuous latent independent variables are free except when they are random effect variables defined by using ON or XWITH in conjunction with the | symbol. In these cases, the covariances among continuous latent independent variables are fixed at zero. In multiple class analysis, free covariances among continuous latent independent variables are equal across classes.
· In single group analysis and multiple group analysis, covariances among continuous latent independent variables and observed independent variables are fixed at zero.
· Covariances among observed variables not explicitly dependent or independent are fixed at zero.
· Residual covariances among observed dependent variables and among continuous latent dependent variables are fixed at zero with the following exceptions:
· In single group analysis and multiple group analysis, residual covariances among observed dependent variables are free when neither variable influences any other variable, when the variables are not factor indicators, and when the variables are either continuous, censored (using weighted least squares), or categorical (using weighted least squares). In multiple class analysis, free residual covariances among observed dependent variables are equal across classes.
· In single group analysis and multiple group analysis, residual covariances among continuous latent dependent variables that are not indicators of a second-order factor are free when neither variable influences any other variable except its own indicators, except when they are random effect variables defined by using ON or XWITH in conjunction with the | symbol. In these cases, the covariances among continuous latent independent variables are fixed at zero. In multiple class analysis, free residual covariances among continuous latent dependent variables are equal across classes.
Following are the default settings for regression coefficients:
· Regression coefficients are fixed at zero unless they are explicitly mentioned in the MODEL command. In multiple group analysis, free regression coefficients are unequal in all groups unless they involve the regression of an observed dependent variable that is used as a factor indicator on a continuous latent variable. In this case, they are free and equal across groups. In multiple class analysis, free regression coefficients are equal across classes.
PARAMETER DEFAULT STARTING VALUES
If a parameter is not free by default, when the parameter is mentioned in the MODEL command, it is free at the default starting value unless another starting value is specified using the asterisk (*) followed by a number or the parameter is fixed using the @ symbol followed by a number. The exception to this is that variances and residual variances for latent response variables corresponding to categorical observed dependent variables cannot be free in the Delta parameterization. They can be free in the Theta parameterization. In the Theta parameterization, scale factors for latent response variables corresponding to categorical observed dependent variables cannot be free. They can be free in the Delta parameterization.
GENERAL DEFAULTS
Following are the default starting values:
Means/intercepts of continuous and 0 or sample mean
censored observed variables depending on the analysis
Means/intercepts of count observed variables 0
Thresholds of categorical observed variables 0 or determined by the
sample proportions
depending on the analysis
Variances/residual variances of .05 or 1 depending on
continuous latent variables the analysis
Variances/residual variances of .5 of the sample
continuous and censored observed variables variance
Variances/residual variances of 1
latent response variables for categorical
observed variables
Scale factors 1
Loadings for indicators of continuous 1
latent variables
All other parameters 0
For situations where starting values depend on the analysis, the starting values can be found using the TECH1 option of the OUTPUT command.
When growth models are specified using the | symbol of the MODEL command and the outcome is continuous or censored, automatic starting values for the growth factor means and variances are generated based on individual regressions of the outcome variable on time. For other outcome types, the defaults above apply.
RANDOM STARTING VALUES FOR MIXTURE MODELS
When TYPE=MIXTURE is specified, the default starting values are automatically generated values that are used to create randomly perturbed sets of starting values for all parameters in the model except variances and covariances.
USER-SPECIFIED STARTING VALUES FOR MIXTURE MODELS
Following are suggestions for obtaining starting values when random starts are not used with TYPE=MIXTURE. User-specified starting values can reduce computation time with STARTS=0. They can be helpful when there is substantive knowledge of the relationship between latent classes and the latent class indicators. For example, it may be well-known that there is a normative class in which individuals have a very low probability of engaging in any of the behaviors represented by the latent class indicators. User-specified starting values may also be used for confirmatory latent class analysis or confirmatory growth mixture modeling.
Starting values for the thresholds of the categorical latent class indicators are given in the logit scale. For ordered categorical latent class indicators, the threshold starting values for each variable must be ordered from low to high. The exception to this is when equality constraints are placed on adjacent thresholds for a variable in which case the same starting value is used. It is a good idea to start the classes apart from each other.
Following is a translation of probabilities to logit threshold values that can be used to help in selecting starting values. Note that logit threshold values have the opposite sign from logit intercept values. The probability is the probability of exceeding a threshold. High thresholds are associated with low probabilities.
Very low probability Logit threshold of +3
Low probability Logit threshold of +1
High probability Logit threshold of -1
Very high probability Logit threshold of -3
In most analyses, it is sufficient to use the default starting values together with random starts. If starting values are needed, the following two strategies are suggested. The first strategy is to estimate the growth model as either a one-class model or a regular growth model to obtain means and standard deviations for the intercept and slope growth factors. These values can be used to compute starting values. For example, starting values for a 2 class model could be the mean plus or minus half of a standard deviation.
The second strategy is to estimate a multi-class model with the variances and covariances of the growth factors fixed at zero. The estimates of the growth factor means from this analysis can be used as starting values in an analysis where the growth factor variances and covariances are not fixed at zero.
MULTIPLE SOLUTIONS FOR MIXTURE MODELS
With mixture models, multiple maxima of the likelihood often exist. It is therefore important to use more than one set of starting values to find the global maximum. If the best (highest) loglikelihood value is not replicated in at least two final stage solutions and preferably more, it is possible that a local solution has been reached, and the results should not be interpreted without further investigation. Following is an example of a set of ten final stage solutions that point to a good solution because all of the final stage solutions have the same loglikelihood value:
Loglikelihood Seed Initial Stage Starts
-836.899 902278 21
-836.899 366706 29
-836.899 903420 5
-836.899 unperturbed 0
-836.899 27071 15
-836.899 967237 48
-836.899 462953 7
-836.899 749453 33
-836.899 637345 19
-836.899 392418 28
Following is an example of a set of final stage solutions that may point to a possible local solution because the best loglikelihood value is not replicated:
Loglikelihood Seed Initial Stage Starts
-835.247 902278 21
-837.132 366706 29
-840.786 903420 5
-840.786 unperturbed 0
-840.786 27071 15
-853.684 967237 48
-867.123 462953 7
-890.442 749453 33
-905.512 637345 19
-956.774 392418 28
Although the loglikelihood value of -840.786 is replicated three times, it points to a local solution because it is not the best loglikelihood value. The best loglikelihood value must be replicated for a trustworthy solution.
When several final stage optimizations result in similar loglikelihood values that are close to the highest loglikelihood value, the parameter estimates for these solutions should be studied using the OPTSEED option of the ANALYSIS command. If the parameter estimates are different across the solutions, this indicates that the model is not well-defined for the data. This may be because too many classes are being extracted. If the parameter values are very similar across the solutions, the solution with the highest loglikelihood should be chosen.
Following is a set of recommendations for an increasingly more thorough investigation of multiple solutions using the STARTS and STITERATIONS options of the ANALYSIS command. The first recommendation is:
STARTS = 100 20;
which increases the number of initial stage random sets of starting values from the default of 20 to 100 and the number of final stage optimizations from the default of 4 to 20. In this recommendation, the default of ten STITERATIONS is used.
A second recommendation is:
STARTS = 100 20;
STITERATIONS = 20;
where STITERATIONS is increased from the default of 10 iterations to 20 iterations in addition to increasing the number of initial stage random sets of starting values and final stage optimizations.
A third recommendation is to increase the initial stage random sets of starting values further to 500, increase the final stage optimizations to 100, with or without increasing STITERATIONS. Following is the specification without increasing STITERATIONS.
STARTS = 500 100;
Some combinations of models and data may cause convergence problems. A message to this effect is found in the output. Convergence problems are often related to variables in the model being measured on very different scales, poor starting values, and/or a model being estimated that is not appropriate for the data. In addition, certain models are more likely to have convergence problems. These include mixture models, two-level models, and models with random effects that have small variances.
GENERAL CONVERGENCE PROBLEMS
It is useful to distinguish between two types of non-convergence. The type of non-convergence can be determined by examining the optimization history of the analysis which is obtained by using the TECH5 and/or TECH8 options of the OUTPUT command. In the first type of non-convergence, the program stops before convergence because the maximum number of iterations has been reached. In the second type of non-convergence, the program stops before the maximum number of iterations has been reached because of difficulties in optimizing the fitting function.
For both types of convergence problems, the first thing to check is that the continuous observed variables are measured on similar scales. Convergence problems can occur when the sample variance values for continuous observed variables fall substantially outside of the range of 1 to 10. This is particularly important with a combination of categorical and continuous observed variables. When variances of continuous observed variables are large, the DEFINE command can be used to divide the variables by a constant. When they are small, the DEFINE command can be used to multiply them by a constant.
In the first type of problem, as long as no large negative variances/residual variances are found in the preliminary parameter estimates and each iteration has not had a large number of trys, convergence may be reached by increasing the number of iterations or using the preliminary parameter estimates as starting values. If there are large negative variances/residual variances, new starting values should be tried. In the second type of problem, the starting values are not appropriate for the model and the data. New starting values should be tried. Starting values for variance/residual variance parameters are the most important to change. If new starting values do not help, the model should be modified.
A useful way to avoid convergence problems due to poor starting values is to build up a model by estimating the model parts separately to obtain appropriate starting values for the full model.
CONVERGENCE PROBLEMS SPECIFIC TO MODELING WITH RANDOM EFFECTS
Random effect models can have convergence problems when the random effect variables have small variances. Problems can arise in models in which random effect variables are defined using the ON or AT options of the MODEL command in conjunction with the | symbol of the MODEL command and in growth models for censored, categorical, and count outcomes. If convergence problems arise, information in the error messages identifies the problematic variable. In addition, the output can be examined to see the size of the random effect variable variance. If it is close to zero and the random effect variable is a random slope defined using an ON statement in conjunction with the | symbol, a fixed effect should be used instead by using a regular ON statement. If it is close to zero and the random effect variable is a growth factor, the growth factor variance and corresponding covariances should be fixed at zero.
CONVERGENCE PROBLEMS SPECIFIC TO MIXTURE MODELS
In mixture models, convergence is determined not only by the derivatives of the loglikelihood but also by the absolute and relative changes in the loglikelihood and the changes in the class counts. Information about changes in the loglikelihood and the class counts can be found in TECH8.
Even when a mixture model does converge, it is possible to obtain a local solution. Therefore, it is important to run the model with multiple sets of starting values to guarantee that the best solution is obtained. The best solution is the solution with the largest loglikelihood. As discussed above, the STARTS option of the ANALYSIS command can be used for automatically generating multiple sets of randomly drawn starting values that are used to find the best solution.
Not all models that can be specified in the program are identified. A non-identified model is one that does not have meaningful estimates for all of its parameters. Standard errors cannot be computed for non-identified models because of a singular Fisher information matrix. When a model is not identified, an error message is printed in the output. In most cases, the error message gives the number of the parameter that contributes to the non-identification. The parameter to which the number applies is found using the TECH1 option of the OUTPUT command. Additional restrictions on the parameters of the model are often needed to make the model identified.
Model identification can be complex for mixture models. Mixture models that are in theory identified can in certain samples and with certain starting values be empirically non-identified. In this situation, changing the starting values or changing the model is recommended.
For all models, model identification can be determined by examining modification indices and derivatives. If a fixed parameter for an outcome has a modification index or a derivative of zero, it will not be identified if it is free. For an estimated model that is known to be identified, the model remains identified if a parameter with a non-zero modification index or a non-zero derivative is freed. Derivatives are obtained by using the TECH2 option of the OUTPUT command. Modification indices are obtained by using the MODINDICES option of the OUTPUT command.
Numerical integration is required for maximum likelihood estimation when the posterior distribution of the latent variable does not have a closed form expression. In the table below, the ON and BY statements that require numerical integration are designated by a single or double asterisk (*). A single asterisk (*) indicates that numerical integration is always required. A double asterisk (*) indicates that numerical integration is required when the mediating variable has missing data. Numerical integration is also required for models with interactions involving continuous latent variables and for certain models with random slopes such as multilevel mixture models.
Scale of Dependent Variable |
Scale of Observed Mediating Variable |
Scale of Latent Variable |
|
|
Continuous |
Censored, Categorical, and Count |
Continuous |
|
|
Continuous |
ON |
ON** |
ON BY |
|
Censored, Categorical, and Count |
ON** |
ON** |
ON* BY* |
|
Nominal |
ON** |
ON** |
ON* |
|
Continuous Latent |
ON |
ON** |
ON BY |
|
Categorical Latent |
ON** |
ON** |
ON* BY* |
|
Inflation Part of Censored and Count |
ON** |
ON** |
ON* BY* |
When the posterior distribution does not have a closed form, it is necessary to integrate over the density of the latent variable multiplied by the conditional distribution of the outcomes given the latent variable. Numerical integration approximates this integration by using a weighted sum over a set of integration points (quadrature nodes) representing values of the latent variable.
Three types of numerical integration are available in Mplus with or without adaptive numerical integration. They are rectangular (trapezoid) numerical integration with a default of 15 integration points per dimension, Gauss-Hermite integration with a default of 15 integration points per dimension, and Monte Carlo integration with integration points generated randomly with a default of 500 integration points in total. In many cases, all three integration types are available. When mediating variables have missing data, only the Monte Carlo integration algorithm is available.
For some analyses it is necessary to increase the number of integration points to obtain sufficient numerical precision. In these cases, 20-50 integration points per dimension are recommended for rectangular and Gauss-Hermite integration and 5000 total integration points for Monte Carlo integration. Going beyond these recommendations is not advisable because the precision is unlikely to be improved any further, computations will become slower, and numerical instability can arise from increased round off error.
In most analyses, the default of adaptive numerical integration is expected to outperform non-adaptive numerical integration. In most analyses, 15 integration points per dimension are sufficient with adaptive numerical integration, whereas non-adaptive numerical integration may require 30-50 integration points per dimension. There are analyses, however, where adaptive numerical integration leads to numerical instability. These include analyses with outliers, non-normality in the latent variable distribution, and small cluster sizes. In such analyses, it is recommended to turn off the adaptive numerical integration using the ADAPTIVE option of the ANALYSIS command.
Numerical integration is computationally heavy and thereby time-consuming because the integration must be done at each iteration, both when computing the function value and when computing the derivative values. The computational burden increases as a function of the number of integration points, increases linearly as a function of the number of observations, and increases exponentially as a function of the number of dimensions of integration. For rectangular and Gauss-Hermite integration, the computational burden also increases exponentially as a function of the dimensions of integration, that is, the number of latent variables, random slopes, or latent variable interactions for which numerical integration is needed. Following is a list that shows the computational burden in terms of the number of dimensions of integration using the default number of integration points.
One dimension of integration Light
Two dimensions of integration Moderate
Three to four dimensions of integration Heavy
Five or more dimensions of integration Very heavy
Note that with several dimensions of integration it may be advantageous to use Monte Carlo integration. Monte Carlo integration may, however, result in loglikelihood values with low numerical precision making the testing of nested models using likelihood ratio chi-square tests based on loglikelihood differences imprecise. To reduce the computational burden with several dimensions of integration, it is sometimes possible to get sufficiently precise results by reducing the number of integration points per dimension from the default of 15 to 10 or 7. For exploratory factor analysis, as few as three integration points per dimension may be sufficient.
PRACTICAL ASPECTS OF NUMERICAL INTEGRATION
Following is a list of suggestions for using numerical integration:
· Start with a model that has a small number of latent variables, random slopes, or latent variable interactions for which numerical integration is required and add to this number in small increments
· Start with an analysis using the TECH8 and TECH1 options of the OUTPUT command in conjunction with the MITERATIONS and STARTS options of the ANALYSIS command set to 1 and 0, respectively, to obtain information on the time required for one iteration and to check that the model specifications are correct
· With more than 3 dimensions of integration, reduce the number of integration points per dimension to 10 or use Monte Carlo integration with 5000 total integration points
· If the TECH8 output shows large negative values in the column labeled ABS CHANGE, increase the number of integration points to improve the precision of the numerical integration and resolve convergence problems
· Because non-identification based on a singular information matrix may be difficult to determine when numerical integration is involved, it is important to check for a low condition number which may indicate non-identification, for example, a condition number less than 1.0E-6
In this section, special issues related to multiple group or multiple population analysis are discussed. Multiple group analysis is used when data from more than one population are being examined to investigate measurement invariance and population heterogeneity. Measurement invariance is investigated by testing the invariance of measurement parameters across groups. Measurement parameters include intercepts or thresholds of the factor indicators, factor loadings, and residual variances of the factor indicators. Population heterogeneity is investigated by testing the invariance of structural parameters across groups. Structural parameters include factor means, variances, and covariances and regression coefficients. Multiple group analysis is not available for TYPE=MIXTURE and EFA. Multiple group analysis for TYPE=MIXTURE can be carried out using the KNOWNCLASS option of the VARIABLE command. Following are the topics discussed in this section:
· Requesting a multiple group analysis
· First group in multiple group analysis
· Defaults for multiple group analysis
· MODEL command in multiple group analysis
· Equalities in multiple group analysis
· Means/intercepts/thresholds in multiple group analysis
· Scale factors in multiple group analysis
· Residual variances of latent response variables in multiple group analysis
· Data in multiple group analysis
· Testing for measurement invariance using multiple group analysis
REQUESTING A MULTIPLE GROUP ANALYSIS
The way to request a multiple group analysis depends on the type of data that are being analyzed. When individual data stored in one data set are analyzed, a multiple group analysis is requested by using the GROUPING option of the VARIABLE command. When individual data stored in different data sets are analyzed, multiple group analysis is requested by using multiple FILE statements in the DATA command. When summary data are analyzed, multiple group analysis is requested by using the NGROUPS option of the DATA command.
FIRST GROUP IN MULTIPLE GROUP ANALYSIS
In some situations it is necessary to know which group the program considers to be the first group. How the first group is defined differs depending on the type of data being analyzed. For individual data in a single data set, the first group is defined as the group with the lowest value on the grouping variable. For example if the grouping variable is gender with males having the value of 1 and females having the value of 0, then the first group is females. For individual data in separate data sets, the first group is the group represented by the first FILE statement listed in the DATA command. For example, if the following FILE statements are specified in an input setup,
FILE (male) IS male.dat;
FILE (female) IS female.dat;
the first group is males. For summary data, the first group is the group with the label, g1. This group is the group represented by the first set of summary data found in the summary data set.
DEFAULTS FOR MULTIPLE GROUP ANALYSIS
In multiple group analysis, some measurement parameters are held equal across the groups as the default. This is done to reflect measurement invariance of these parameters. Intercepts, thresholds, and factor loadings are held equal across groups. The residual variances of the factor indicators are not held equal across groups.
All structural parameters are free and not constrained to be equal across groups as the default. Structural parameters include factor means, variances, and covariances and regressions coefficients. Factor means are fixed at zero in the first group and are free to be estimated in the other groups as the default. This is because factor means generally cannot be identified for all groups. The customary approach is to set the factor means to zero in a reference group, here the first group.
For observed categorical dependent variables using the default Delta parameterization, the scale factors of the latent response variables of the categorical factor indicators are fixed at one in the first group and are free to be estimated in the other groups as the default. This is because the latent response variables are not restricted to have across-group equalities of variances. For observed categorical dependent variables using the Theta parameterization, the residual variances of the latent response variables of the categorical factor indicators are fixed at one in the first group and are free to be estimated in the other groups as the default.
MODEL COMMAND IN MULTIPLE GROUP ANALYSIS
In multiple group analysis, two variations of the MODEL command are used. They are MODEL and MODEL followed by a label. MODEL is used to describe the overall analysis model. MODEL followed by a label is used to describe differences between the overall analysis model and the analysis model for each group. These are referred to as group-specific models. The labels are defined using the GROUPING option of the VARIABLE command for individual data in a single file, by the FILE options of the DATA command for individual data in separate files, and by the program for summary data and Monte Carlo simulation studies. It is not necessary to describe the full model for each group in the group-specific models. Group-specific models should contain only differences from the model described in the overall MODEL command and the model for that group.
Following is an example of an overall MODEL command for multiple group analysis:
MODEL: f1 BY y1 y2 y3;
f2 BY y4 y5 y6;
In the above overall MODEL command, the two BY statements specify that f1 is measured by y1, y2, and y3, and f2 is measured by y4, y5, and y6. The metric of the factors is set automatically by the program by fixing the first factor loading in each BY statement to 1. The intercepts of the factor indicators and the other factor loadings are held equal across the groups as the default. The residual variances are estimated for each group and the residual covariances are fixed at zero as the default. Factor variances and the factor covariance are estimated for each group.
Following is a group-specific MODEL command that relaxes the equality constraints on the factor loadings in a two-group analysis:
MODEL g2: f1 BY y2 y3;
f2 BY y5 y6;
In the above group-specific MODEL command, the equality constraints on the factor loadings of y2, y3, y5, and y6 are relaxed by including them in a group-specific MODEL command. The first factor indicator of each factor should not be included because including them frees their factor loadings which should be fixed at one to set the metric of the factors.
Factor means are fixed at zero in the first group and are estimated in each of the other groups. The following group-specific MODEL command relaxes the equality constraints on the intercepts and thresholds of the observed dependent variables:
MODEL g2: [y1 y2 y3];
[u4$1 u5$2 u6$3];
Following is a set of MODEL commands for a multiple group analysis in which three groups are being analyzed: g1, g2, and g3:
MODEL: f1 BY y1-y5;
f2 BY y6-y10;
f1 ON f2;
MODEL g1: f1 BY y5;
MODEL g2: f2 BY y9;
In the overall MODEL command, the first BY statement specifies that f1 is measured by y1, y2, y3, y4, and y5. The second BY statement specifies that f2 is measured by y6, y7, y8, y9, and y10. The metric of the factors is set automatically by the program by fixing the first factor loading in each BY statement to one. The intercepts of the factor indicators and the other factor loadings are held equal across the groups as the default. The residual variances for y1 through y10 are estimated for each group and the residual covariances are fixed at zero as the default. The variance of the factor f2 and the residual variance of the factor f1 are estimated for each group. A regression coefficient for the linear regression of f1 on f2 is estimated for each group.
Differences between the overall model and the group-specific models are specified using the MODEL command followed by a label. The two group-specific MODEL commands above specify differences between the overall model and the group-specific models. In the above example, the factor loading for y5 in group g1 is not constrained to be equal to the factor loading for y5 in the other two groups and the factor loading for y9 in group g2 is not constrained to be equal to the factor loading for y9 in the other two groups. The model for g3 is identical to that of the overall model because there is no group-specific model statement for g3.
EQUALITIES IN MULTIPLE GROUP ANALYSIS
A number or list of numbers in parentheses following a parameter or list of parameters is used to indicate equality constraints. Constraining parameters to be equal in a single group analysis is discussed in Chapter 17. In a single group analysis, parameters are constrained to be equal by placing the same number or list of numbers in parentheses following the parameters that are to be held equal. For example,
y1 ON x1 (1) ;
y2 ON x2 (1) ;
y3 ON x3 (2) ;
y4 ON x4 (2) ;
y5 ON x5 (2) ;
constrains the regression coefficients of the first two equations to be equal and the regression coefficients of the last three equations to be equal.
In multiple group analysis, the interpretation of equality constraints depends on whether they are part of the overall MODEL command or a group-specific MODEL command. Equality constraints specified in the overall MODEL command apply to all groups. Equality constraints specified in a group-specific MODEL command apply to only that group.
Following is an example of how to specify across group equality constraints in the overall MODEL command:
MODEL: f1 BY y1-y5;
y1 (1)
y2 (2)
y3 (3)
y4 (4)
y5 (5);
By placing a different number in parentheses after each residual variance, each residual variance is held equal across all groups but not equal to each other. Note that only one equality constraint can be specified per line.
Following is another example of how to specify across group equality constraints in the overall MODEL command:
MODEL: f1 BY y1-y5;
y1-y5 (1);
By placing a one in parentheses after the list of residual variances, y1 through y5, the values of those parameters are held equal to each other and across groups. If the five residual variances are free to be estimated across the three groups, there are fifteen parameters. With the equality constraint, one parameter is estimated.
Following is an example of how to specify an equality constraint in a group-specific MODEL command:
MODEL g2: y1-y5 (2);
In the group-specific MODEL command for g2, the residual variances of y1 through y5 are held equal for g2 but are not held equal to the residual variances of any other group because (2) is not specified in the overall MODEL command or in any other group-specific MODEL command. One residual variance is estimated for g2.
Following is an example of how to relax an equality constraint in a group-specific MODEL command:
MODEL g3: y1-y5;
In this example, by mentioning the residual variances in a group-specific MODEL command, they are no longer held equal to the residual variances in groups 1 and 3. Five residual variances are estimated for g3.
The overall and group-specific MODEL commands discussed above are shown and interpreted together below:
MODEL: f1 BY y1-y5;
y1-y5 (1);
MODEL g2: y1-y5 (2);
MODEL g3: y1-y5;
The overall MODEL command specifies the overall model for the three groups as described above. Because there is no group-specific MODEL command for g1, g1 uses the same model as that described in the overall MODEL command. The group-specific MODEL commands describe the differences between the overall model and the group-specific models. The group g2 uses the overall model with the exception that the one residual variance that is estimated is not constrained to be equal to the other two groups. The group g3 uses the overall model with the exception that five residual variances not constrained to be equal to the other groups are estimated.
MEANS/INTERCEPTS/THRESHOLDS IN MULTIPLE GROUP ANALYSIS
In multiple group analysis, the intercepts and thresholds of observed dependent variables that are factor indicators are constrained to be equal across groups as the default. The means and intercepts of continuous latent variables are fixed at zero in the first group and are free to be estimated in the other groups as the default. Means, intercepts, and thresholds are referred to by the use of square brackets.
Following is an example how to refer to means and intercepts in a multiple group model.
MODEL: f1 BY y1-y5;
f2 BY y6-y10;
f1 ON f2;
MODEL g1: [f1 f2];
MODEL g2: [f1@0 f2@0];
In the above example, the intercepts and the factor loadings for the factor indicators y1-y5 are held equal across the three groups as the default. In the group-specific MODEL command for g1, the mean of f2 and the intercept of f1 are specified to be free. In the group-specific MODEL command for g2, the mean of f2 and the intercept of f1 are fixed at zero.
The following group-specific MODEL command relaxes the equality constraints on the intercepts of the observed dependent variables:
MODEL g2: [y1-y10];
SCALE FACTORS IN MULTIPLE GROUP ANALYSIS
Scale factors can be used in multiple group analysis. They are recommended when observed dependent variables are categorical and a weighted least squares estimator is used. They capture across group differences in the variances of the latent response variables for the observed categorical dependent variables. Scale factors are part of the model as the default using a weighted least squares estimator when one or more observed dependent variables are categorical. In this situation, the first group has scale factors fixed at one. In the other groups, scale factors are free to be estimated with starting values of one. Scale factors are referred to using curly brackets. Following is an example of how to refer to scale factors in a model with multiple groups where u1, u2, u3, u4, and u5 are observed categorical dependent variables:
MODEL: f BY u1-u5;
MODEL g2: {u1-u5*.5};
In the above example, the scale factors of the latent response variables of the observed categorical dependent variables in g1 are fixed at one as the default. Starting values are given for the free scale factors in g2.
RESIDUAL VARIANCES OF LATENT RESPONSE VARIABLES IN MULTIPLE GROUP ANALYSIS
With the Theta parameterization for observed categorical dependent variables using a weighted least squares estimator, residual variances of the latent response variables for the observed categorical dependent variables are part of the model as the default. In this situation, the first group has residual variances fixed at one for all observed categorical dependent variables. In the other groups, residual variances are free to be estimated with starting values of one. Residual variances of the latent response variables are referred to using the name of the corresponding observed variable. Following is an example of how to refer to residual variances in a model with multiple groups where u1, u2, u3, u4, and u5 are observed categorical dependent variables:
MODEL: f BY u1-u5;
MODEL g2: u1-u5*2;
In the above example, the residual variances of the latent response variables of the observed categorical dependent variables in g1 are fixed at one as the default. Starting values are given for the free residual variances in g2.
DATA IN MULTIPLE GROUP ANALYSIS
One difference between single group analysis and multiple group analysis is related to the data to be analyzed. For individual data, the data for all groups can be stored in one data set or in different data sets. If the data are stored in one data set, the data set must include a variable that identifies the group to which each observation belongs. For summary data, all data must be stored in the same data set.
If individual data for several groups are stored in one data set, the data set must include a variable that identifies the group to which each observation belongs. The name of this variable is specified using the GROUPING option of the VARIABLE command. Only one grouping variable can be specified. If the groups to be analyzed are a combination of more than one variable, for example, gender and ethnicity, a single grouping variable can be created using the DEFINE command. An example of how to specify the GROUPING option is:
GROUPING IS gender (1 = male 2 = female);
The information in parentheses after the grouping variable name assigns labels to the values of the grouping variable found in the data set. In the example above, observations with the variable gender equal to 1 are assigned the label male, and observations with the variable gender equal to 2 are assigned the label female. These labels are used in group-specific MODEL commands to specify differences between the overall model and the group-specific models. If an observation has a value for the grouping variable that is not specified using the GROUPING option, it is not included in the analysis.
INDIVIDUAL DATA, DIFFERENT DATA SETS
For individual data stored in different data sets, the specification of the FILE option of the DATA command has two differences for multiple group analysis. First, a FILE statement is required for each data set. Second, the FILE option allows a label to be specified that can be used in the group-specific MODEL commands. In the situation where the data for males are stored in a file named male.dat, and the data for females are stored in a file named female.dat, the FILE option is specified as follows:
FILE (male) = male.dat;
FILE (female) = female.dat;
The labels male and female can be used in the group-specific MODEL commands to specify differences between the group-specific models for males and females and the overall model.
When individual data are stored in different data sets, all of the data sets must contain the same number of variables. These variables must be assigned the same names and be read using the same format.
Summary data must be stored in one data set with the data for the first group followed by the data for the second group, etc.. For example, in an analysis of means and a covariance matrix for two groups with four observed variables, the data would appear as follows:
0 0 0 0
2
1 2
1 1 2
1 1 1 2
1 1 1 1
3
2 3
2 2 3
2 2 2 3
where the means for group 1 come first, followed by the covariances for group 1, followed by the means for group 2, followed by the covariances for group 2.
The NOBSERVATIONS and NGROUPS options have special formats for multiple group analysis when summary data are analyzed. The NOBSERVATIONS option requires an entry for each group in the order that the data appear in the data set. For example, if the summary data for males appear first in a data set followed by the summary data for females, the NOBSERVATIONS statement,
NOBSERVATIONS = 180 220;
indicates that the summary data for males come from 180 observations and the summary data for females come from 220 observations.
In addition, for summary data, it is necessary to specify the number of groups in the analysis using the NGROUPS option of the DATA command. The format of this option follows:
NGROUPS = 2;
which indicates that there are two groups in the analysis. For summary data, the program automatically assigns the label g1 to the first group, g2 to the second group, etc. In this example, males would have the label g1 and females would have the label g2.
TESTING FOR MEASUREMENT INVARIANCE USING MULTIPLE GROUP ANALYSIS
Multiple group analysis can be used to test measurement invariance of factors using chi-square difference tests or loglikelihood difference tests for a set of nested models. For continuous, censored, and count variables, the measurement parameters are the intercepts, factor loadings, and residual variances of the factor indicators. In many disciplines, invariance of intercepts or thresholds and factor loadings are considered sufficient for measurement invariance. Some disciplines also require invariance of residual variances. For categorical variables, the measurement parameters are thresholds and factor loadings. For the Delta parameterization of weighted least squares estimation, scale factors can also be considered. For the Theta parameterization of weighted least squares estimation, residual variances can also be considered.
Following is a description of the models to be used to test for measurement invariance for various variable types and estimators. These models can also be used to test for longitudinal measurement invariance. Necessary restrictions are placed across time rather than across groups.
MODELS FOR CONTINUOUS, CENSORED, AND COUNT VARIABLES
Following is a set of models that can be considered for measurement invariance of continuous, censored, and count variables. They are listed from least restrictive to most restrictive.
For continuous, censored, and count variables, the configural model has factor loadings, intercepts, and residual variances free across groups and factor means fixed at zero in all groups. If the metric of a factor is set by fixing a factor loading to one, factor variances are free across groups. If the metric of a factor is set by freeing all factor loadings and fixing the factor variance to one, the factor variance is fixed at one in all groups.
The metric has factor loadings constrained to be equal across groups, intercepts and residual variances free across groups, and factor means fixed at zero in all groups. If the metric of a factor is set by fixing a factor loading to one, factor variances are free across groups. If the metric of a factor is set by freeing all factor loadings within a group and fixing the factor variance to one, the factor variance is fixed at one in one group and is free in the other groups.
The scalar model has factor loadings and intercepts constrained to be equal across groups, residual variances free across groups, and factor means fixed at zero in one group and free in the other groups. If the metric of a factor is set by fixing a factor loading to one, factor variances are free across groups. If the metric of a factor is set by freeing all factor loadings within a group and fixing the factor variance to one, the factor variance is fixed at one in one group and is free in the other groups.
MODELS FOR BINARY VARIABLES
Following is a set of models that can be considered for measurement invariance of binary variables. They are listed from least restrictive to most restrictive. For binary variables and weighted least squares estimation, only the configural and scalar models are considered. The metric model is not identified because scale factors or residual variances are allowed to vary across groups. For binary variables and maximum likelihood estimation, the configural, metric, and scalar models are considered. The metric model is identified because residual variances are implicitly fixed at one in all groups.
WEIGHTED LEAST SQUARES ESTIMATION USING THE DELTA PARAMETERIZATION
For binary variables using weighted least squares estimation and the Delta parameterization, the configural model has factor loadings and thresholds free across groups, scale factors fixed at one in all groups, and factor means fixed at zero in all groups. If the metric of a factor is set by fixing a factor loading to one, factor variances are free across groups. If the metric of a factor is set by freeing all factor loadings and fixing the factor variance to one, the factor variance is fixed at one in all groups.
The scalar model has factor loadings and thresholds constrained to be equal across groups, scale factors fixed at one in one group and free in the other groups, and factor means fixed at zero in one group and free in the other groups. If the metric of a factor is set by fixing a factor loading to one, factor variances are free across groups. If the metric of a factor is set by freeing all factor loadings within a group and fixing the factor variance to one, the factor variance is fixed at one in one group and is free in the other groups.
WEIGHTED LEAST SQUARES ESTIMATION USING THE THETA PARAMETERIZATION
For binary variables using weighted least squares estimation and the Theta parameterization, the configural model has factor loadings and thresholds free across groups, residual variances fixed at one in all groups, and factor means fixed at zero in all groups. If the metric of a factor is set by fixing a factor loading to one, factor variances are free across groups. If the metric of a factor is set by freeing all factor loadings and fixing the factor variance to one, the factor variance is fixed at one in all groups.
The scalar model has factor loadings and thresholds constrained to be equal across groups, residual variances fixed at one in one group and free in the other groups, and factor means fixed at zero in one group and free in the other groups. If the metric of a factor is set by fixing a factor loading to one, factor variances are free across groups. If the metric of a factor is set by freeing all factor loadings within a group and fixing the factor variance to one, the factor variance is fixed at one in one group and is free in the other groups.
MAXIMUM LIKELIHOOD ESTIMATION
For binary variables and maximum likelihood estimation, the configural model has factor loadings and thresholds free across groups and factor means fixed at zero in all groups. If the metric of a factor is set by fixing a factor loading to one, factor variances are free across groups. If the metric of a factor is set by freeing all factor loadings and fixing the factor variance to one, the factor variance is fixed at one in all groups.
The metric model has factor loadings constrained to be equal across groups, thresholds free across groups, and factor means fixed at zero in all groups. If the metric of a factor is set by fixing a factor loading to one, factor variances are free across groups. If the metric of a factor is set by freeing all factor loadings within a group and fixing the factor variance to one, the factor variance is fixed at one in one group and is free in the other groups.
The scalar model has factor loadings and thresholds constrained to be equal across groups and factor means fixed at zero in one group and free in the other groups. If the metric of a factor is set by fixing a factor loading to one, factor variances are free across groups. If the metric of a factor is set by freeing all factor loadings within a group and fixing the factor variance to one, the factor variance is fixed at one in one group and is free in the other groups.
MODELS FOR ORDERED CATEGORICAL (ORDINAL) VARIABLES
Following is a set of models that can be considered for measurement invariance of ordered categorical (ordinal) variables. They are listed from least restrictive to most restrictive. The metric model is not allowed for ordered categorical (ordinal) variables when a factor indicator loads on more than one factor, when the metric of a factor is set by fixing a factor variance to one, and when Exploratory Structural Equation Modeling (ESEM) is used.
WEIGHTED LEAST SQUARES ESTIMATION USING THE DELTA PARAMETERIZATION
For ordered categorical (ordinal) variables using weighted least squares estimation and the Delta parameterization, the configural model has factor loadings and thresholds free across groups, scale factors fixed at one in all groups, and factor means fixed at zero in all groups. If the metric of a factor is set by fixing a factor loading to one, factor variances are free across groups. If the metric of a factor is set by freeing all factor loadings and fixing the factor variance to one, the factor variance is fixed at one in all groups.
The metric model has factor loadings constrained to be equal across groups, scale factors fixed at one in one group and free in the other groups, and factor means fixed at zero in one group and free in the other groups. The first threshold of each item is held equal across groups. The second threshold of the item that is used to set the metric of the factor is held equal across groups. Factor variances are free across groups. For a discussion of these specifications, see Millsap (2011).
The scalar model has factor loadings and thresholds constrained to be equal across groups, scale factors fixed at one in one group and free in the other groups, and factor means fixed at zero in one group and free in the other groups. If the metric of a factor is set by fixing a factor loading to one, factor variances are free across groups. If the metric of a factor is set by freeing all factor loadings within a group and fixing the factor variance to one, the factor variance is fixed at one in one group and is free in the other groups.
WEIGHTED LEAST SQUARES ESTIMATION USING THE THETA PARAMETERIZATION
For ordered categorical (ordinal) variables using weighted least squares estimation and the Theta parameterization, the configural model has factor loadings and thresholds free across groups, residual variances fixed at one in all groups, and factor means fixed at zero in all groups. If the metric of a factor is set by fixing a factor loading to one, factor variances are free across groups. If the metric of a factor is set by freeing all factor loadings and fixing the factor variance to one, the factor variance is fixed at one in all groups.
The metric model has factor loadings constrained to be equal across groups, residual variances fixed at one in one group and free in the other groups, and factor means fixed at zero in one group and free in the other groups. The first threshold of each item is held equal across groups. The second threshold of the item that is used to set the metric of the factor is held equal across groups. Factor variances are free across groups. For a discussion of these specifications, see Millsap (2011).
The scalar model has factor loadings and thresholds constrained to be equal across groups, residual variances fixed at one in one group and free in the other groups, and factor means fixed at zero in one group and free in the other groups. If the metric of a factor is set by fixing a factor loading to one, factor variances are free across groups. If the metric of a factor is set by freeing all factor loadings within a group and fixing the factor variance to one, the factor variance is fixed at one in one group and is free in the other groups.
MAXIMUM LIKELIHOOD ESTIMATION
For ordered categorical variables and maximum likelihood estimation, the configural model has factor loadings and thresholds free across groups and factor means fixed at zero in all groups. If the metric of a factor is set by fixing a factor loading to one, factor variances are free across groups. If the metric of a factor is set by freeing all factor loadings and fixing the factor variance to one, the factor variance is fixed at one in all groups.
The metric model has factor loadings constrained to be equal across groups, thresholds free across groups, and factor means fixed at zero in all groups. If the metric of a factor is set by fixing a factor loading to one, factor variances are free across groups. If the metric of a factor is set by freeing all factor loadings within a group and fixing the factor variance to one, the factor variance is fixed at one in one group and is free in the other groups.
The scalar model has factor loadings and thresholds constrained to be equal across groups and factor means fixed at zero in one group and free in the other groups. If the metric of a factor is set by fixing a factor loading to one, factor variances are free across groups. If the metric of a factor is set by freeing all factor loadings within a group and fixing the factor variance to one, the factor variance is fixed at one in one group and is free in the other groups.
PARTIAL MEASUREMENT INVARIANCE
When full measurement invariance does not hold, partial measurement invariance can be considered. This involves relaxing some equality constraints on the measurement parameters. For continuous variables, equality constraints can be relaxed for the intercepts, factor loadings, and residual variances. This is shown in Example 5.15. For categorical variables, equality constraints for thresholds and factor loadings for a variable should be relaxed in tandem. In addition, for the Delta parameterization, the scale factor must be fixed at one for that variable. This is shown in Example 5.16. For the Theta parameterization, the residual variance must be fixed at one for that variable. This is shown in Example 5.17.
In chi-square difference testing of measurement invariance, the chi-square value and degrees of freedom of the less restrictive model are subtracted from the chi-square value and degrees of freedom of the nested, more restrictive model. The chi-square difference value is compared to the chi-square value in a chi-square table using the difference in degrees of freedom between the more restrictive and less restrictive models. If the chi-square difference value is significant, it indicates that constraining the parameters of the nested model significantly worsens the fit of the model. This indicates measurement non-invariance. If the chi-square difference value is not significant, this indicates that constraining the parameters of the nested model did not significantly worsen the fit of the model. This indicates measurement invariance of the parameters constrained to be equal in the nested model.
For models where chi-square is not available, difference testing can be done using -2 times the difference of the loglikelihoods. For the MLR, MLM, and WLSM estimators, difference testing must be done using the scaling correction factor printed in the output. A description of how to do this is posted on the website. For WLSMV and MLMV, difference testing must be done using the DIFFTEST option of the SAVEDATA and ANALYSIS commands.
Mplus has several options for the estimation of models with missing data. Mplus provides maximum likelihood estimation under MCAR (missing completely at random) and MAR (missing at random; Little & Rubin, 2002) for continuous, censored, binary, ordered categorical (ordinal), unordered categorical (nominal), counts, or combinations of these variable types. MAR means that missingness can be a function of observed covariates and observed outcomes. For censored and categorical outcomes using weighted least squares estimation, missingness is allowed to be a function of the observed covariates but not the observed outcomes. When there are no covariates in the model, this is analogous to pairwise present analysis. Non-ignorable missing data modeling is possible using maximum likelihood estimation where categorical outcomes are indicators of missingness and where missingness can be predicted by continuous and categorical latent variables (Muthén, Jo, & Brown, 2003; Muthén et al., 2011). Robust standard errors and chi-square are available for all outcomes using the MLR estimator. For non-normal continuous outcomes, this gives the T2* chi-square test statistic of Yuan and Bentler (2000).
Mplus provides multiple imputation of missing data using Bayesian analysis (Rubin, 1987; Schafer, 1997). Both unrestricted H1 and restricted H0 models can be used for imputation.
Multiple data sets generated using multiple imputation (Rubin, 1987; Schafer, 1997) can be analyzed using a special feature of Mplus. Parameter estimates are averaged over the set of analyses, and standard errors are computed using the average of the standard errors over the set of analyses and the between analysis parameter estimate variation.
In all models, missingness is not allowed for the observed covariates because they are not part of the model. The model is estimated conditional on the covariates and no distributional assumptions are made about the covariates. Covariate missingness can be modeled if the covariates are brought into the model and distributional assumptions such as normality are made about them. With missing data, the standard errors for the parameter estimates are computed using the observed information matrix (Kenward & Molenberghs, 1998). Bootstrap standard errors and confidence intervals are also available with missing data.
With missing data, it is useful to do a descriptive analysis to study the percentage of missing data as a first step. This can be accomplished by specifying TYPE=BASIC in the ANALYSIS command. The output for this analysis produces the number of missing data patterns and the proportion of non-missing data, or coverage, for variables and pairs of variables. A default of .10 is used as the minimum coverage proportion for a model to be estimated. This minimum value can be changed by using the COVERAGE option of the ANALYSIS command.
DATA MISSING BY DESIGN
Data missing by design occurs when the study determines which subjects will be observed on which measures. One example is when different forms of a measurement instrument are administered to randomly selected subgroups of individuals. A second example is when it is expensive to collect data on all variables for all individuals and only a subset of variables is measured for a random subgroup of individuals. A third example is multiple cohort analysis where individuals who are measured repeatedly over time represent different birth cohorts. These types of studies can use the missing data method where all individuals are used in the analysis, including those who have missing values on some of the analysis variables by design. This type of analysis is obtained by identifying the values in the data set that are considered to be missing value flags using the MISSING option of the VARIABLE command and identifying the variables for which individuals should have a value using the PATTERN option of the VARIABLE command.
MULTIPLE COHORT DESIGN
Longitudinal research studies often collect data on several different groups of individuals defined by their birth year or cohort. This allows the study of development over a wider age range than the length of the study and is referred to as an accelerated or sequential cohort design. The interest in these studies is the development of an outcome over age not measurement occasion. When dependent variables are measured using a continuous scale, options are available for rearranging such a data set so that age rather than time of measurement is the time variable. This is available only for TYPE=GENERAL without ALGORITHM=INTEGRATION.
The DATA COHORT command is used to rearrange longitudinal data from a format where time points represent measurement occasions to a format where time points represent age or another time-related variable. It is necessary to know the cohort (birth year) of each individual and the year in which each measurement was taken. The difference between measurement year and cohort year is the age of the individual at the time of measurement. Age is the variable that is used to determine the pattern of missing values for each cohort. If an individual does not have information for a particular age, that value is missing for that individual. The transformed data set is analyzed using maximum likelihood estimation for missing data.
REARRANGEMENT OF THE MULTIPLE COHORT DATA
What is of interest in multiple cohort analysis is not how a variable changes from survey year to survey year, but how it changes with age. What is needed to answer this question is a data set where age is the time variable. Following is an example of how a data set is transformed using the DATA COHORT command. In the following data set, the variable heavy drinking (HD) is measured in 1982, 1983, 1987, and 1989. Missing data are indicated with an asterisk (*). The respondents include individuals born in 1963, 1964, and 1965. Although the respondents from any one cohort are measured on only four occasions, the cohorts taken together cover the ages 17 through 26.
Observation |
Cohort |
HD82 |
HD83 |
HD87 |
HD89 |
|
1 |
63 |
3 |
4 |
5 |
6 |
|
2 |
63 |
* |
6 |
7 |
8 |
|
3 |
63 |
9 |
8 |
* |
3 |
|
4 |
63 |
5 |
7 |
6 |
3 |
|
5 |
63 |
5 |
8 |
7 |
9 |
|
6 |
64 |
3 |
6 |
5 |
9 |
|
7 |
64 |
3 |
8 |
* |
5 |
|
8 |
64 |
4 |
9 |
8 |
6 |
|
9 |
64 |
4 |
* |
6 |
7 |
|
10 |
64 |
3 |
9 |
8 |
5 |
|
11 |
65 |
* |
4 |
5 |
6 |
|
12 |
65 |
6 |
5 |
5 |
5 |
|
13 |
65 |
5 |
5 |
5 |
5 |
|
14 |
65 |
4 |
5 |
6 |
7 |
|
15 |
65 |
4 |
5 |
5 |
4 |
The information in the table above represents how the data look before they are transformed. As a first step, each observation that does not have complete data for 1982, 1983, 1987, and 1989 is deleted from the data set. Following is the data after this step.
|
Observation |
Cohort |
HD82 |
HD83 |
HD87 |
HD89 |
|
1 |
63 |
3 |
4 |
5 |
6 |
|
4 |
63 |
5 |
7 |
6 |
3 |
|
5 |
63 |
5 |
8 |
7 |
9 |
|
6 |
64 |
3 |
6 |
5 |
9 |
|
8 |
64 |
4 |
9 |
8 |
6 |
|
10 |
64 |
3 |
9 |
8 |
5 |
|
12 |
65 |
6 |
5 |
5 |
5 |
|
13 |
65 |
5 |
5 |
5 |
5 |
|
14 |
65 |
4 |
5 |
6 |
7 |
|
15 |
65 |
4 |
5 |
5 |
4 |
The second step is to rearrange the data so that age is the time dimension. This results in the following data set where asterisks (*) represent values that are missing by design.
|
Obs |
Coh |
HD17 |
HD18 |
HD19 |
HD20 |
HD22 |
HD23 |
HD24 |
HD25 |
HD26 |
|
1 |
63 |
* |
* |
3 |
4 |
* |
* |
5 |
* |
6 |
|
4 |
63 |
* |
* |
5 |
7 |
* |
* |
6 |
* |
3 |
|
5 |
63 |
* |
* |
5 |
8 |
* |
* |
7 |
* |
9 |
|
6 |
64 |
* |
3 |
6 |
* |
* |
5 |
* |
9 |
* |
|
8 |
64 |
* |
4 |
9 |
* |
* |
8 |
* |
6 |
* |
|
10 |
64 |
* |
3 |
9 |
* |
* |
8 |
* |
5 |
* |
|
12 |
65 |
6 |
5 |
* |
* |
5 |
* |
5 |
* |
* |
|
13 |
65 |
5 |
5 |
* |
* |
5 |
* |
5 |
* |
* |
|
14 |
65 |
4 |
5 |
* |
* |
6 |
* |
7 |
* |
* |
|
15 |
65 |
4 |
5 |
* |
* |
5 |
* |
4 |
* |
* |
The model is specified in the MODEL command using the new variables hd17 through hd26 instead of the original variables hd82, hd83, hd87, and hd89. Note that there is no hd21 because no combination of survey year and birth cohort represents this age. The data are analyzed using the missing by design feature.
The treatment of categorical mediating variables in model estimation differs depending on the estimator being used. Consider the following model:
x -> u -> y
where u is a categorical variable. The issue is how is u treated when it is a dependent variable predicted by x and how is it treated when it is an independent variable predicting y. With weighted least squares estimation, a probit regression coefficient is estimated in the regression of u on x. In the regression of y on u, the continuous latent response variable u* is used as the covariate. With maximum likelihood estimation, either a logistic or probit regression coefficient is estimated in the regression of u on x. In the regression of y on u, the observed variable u is used as the covariate. With Bayesian estimation, a probit regression coefficient is estimated in the regression of u on x. In the regression of y on u, either the observed variable u or the latent response variable u* can be used as the covariate using the MEDIATOR option of the ANALYSIS command.
Following is a description of how to translate probit regression coefficients to probability values. For a treatment of probit regression for binary and ordered categorical (ordinal) variables, see Agresti (1996, 2002).
For a binary dependent variable, the probit regression model expresses the probability of u given x as,
P (u = 1 | x) = F (a + b*x)
= F (-t + b*x),
where F is the standard normal distribution function, a is the probit regression intercept, b is the probit regression slope, t is the probit threshold where t = -a, and P (u = 0 | x) = 1 – P (u = 1 | x).
Following is an output excerpt that shows the results from the probit regression of a binary variable u on the covariate age:
Estimates S.E. Est./S.E.
u ON
age 0.055 0.001 43.075
Thresholds
u$1 3.581 0.062 57.866
Using the formula shown above, the probability of u = 1 for age = 62 is computed as follows:
P (u = 1 | x = 62) = F (-3.581 + 0.055*62)
= F (-0.171).
Using the z table, the value -0.171 corresponds to a probability of approximately 0.43. This means that the probability of u = 1 at age 62 is 0.43.
For an ordered categorical (ordinal) dependent variable with three categories, the probit regression model expresses the probability of u given x using the two thresholds t1 and t2 and the single probit regression coefficient b,
P (u = 0 | x) = F (t1 - b*x),
P (u = 1 | x) = F (t2 - b*x) - F (t1 - b*x),
P (u = 2 | x) = F (- t2 + b*x).
Following is a description of how to translate logistic regression coefficients to probability values. Also described is how to interpret the coefficient estimates in terms of log odds, odds, and odds ratios. For a treatment of logistic regression for binary, ordered categorical (ordinal), and unordered categorical (nominal) variables, see Agresti (1996, 2002) and Hosmer and Lemeshow (2000).
An odds is a ratio of two probabilities. A log odds is therefore the log of a ratio of two probabilities. The exponentiation of a log odds is an odds. A logistic regression coefficient is a log odds which is also referred to as a logit.
For a binary dependent variable u, the logistic regression model expresses the probability of u given x as,
(1) P (u = 1 | x) = exp (a + b*x) / (1 + exp (a + b*x) )
= 1 / (1 + exp (-a – b*x)),
where P (u = 0 | x) = 1 – P (u = 1 | x). The probability expression in (1) results in the linear logistic regression expression also referred to as a log odds or logit,
log [P (u = 1 | x) / P (u = 0 | x)] = log [exp (a + b*x)] = a + b*x,
where b is the logistic regression coefficient which is interpreted as the increase in the log odds of u = 1 versus u = 0 for a unit increase in x. For example, consider the x values of x0 and x0 + 1. The corresponding log odds are,
log odds (x0) = a + b*x0,
log odds (x0 +1) = a + b*(x0 + 1) = a + b*x0 + b,
such that the increase from x0 to x0 + 1 in the log odds is b. The corresponding odds increase is exp (b). For example, consider the continuous covariate age with a logistic regression coefficient of .75 for a dependent variable of being depressed (u = 1) or not being depressed (u = 0). This means that for an increase of one year of age the log odds of being depressed versus not being depressed increases by .75. The corresponding odds increase is 2.12.
For a binary covariate x scored as 0 and 1, the log odds for u = 1 versus u = 0 are,
log odds (x = 0) = a + b*0,
log odds (x = 1) = a + b*1,
such that the increase in the log odds is b as above. Given the mathematical rule that log y – log z is equal to log (y / z), the difference in the two log odds,
b = log odds (x = 1) – log odds (x = 0)
= log [odds (x = 1) / odds (x = 0)],
is the log odds ratio for u = 1 versus u = 0 when comparing x = 1 to x = 0. For example, consider the binary covariate gender (1 = female, 0 = male) with a logistic regression coefficient of 1.0 for a dependent variable of being depressed (u = 1) or not being depressed (u = 0). This means that the log odds for females is 1.0 higher than the log odds for males for being depressed versus not being depressed. The corresponding odds ratio is 2.72, that is the odds for being depressed versus not being depressed is 2.72 times larger for females than for males.
In the case of a binary dependent variable, it is customary to let the first category u = 0 be the reference category as is done in (1). When a dependent variable has more than two categories, it is customary to let the last category be the reference category as is done below. For an unordered categorical (nominal) variable with more than two categories R, the probability expression in (1) generalizes to the following multinomial logistic regression,
(2) P (u = r | x) = exp (ar + br*x) / (exp (a1 + b1*x) + …
+ exp (aR + bR*x)),
where exp (aR + bR*x) = exp (0 + 0*x) = 1 and the log odds for comparing category r to category R is
(3) log [P (u = r | x)/P (u = R | x)] = ar + br*x.
With an ordered categorical (ordinal) variable, the logistic regression slopes br are the same across the categories of u.
Following is an example of an unordered categorical (nominal) dependent variable that is the categorical latent variable in the model. The categorical latent variable has four classes and there are three covariates. The output excerpt shows the results from the multinomial logistic regression of the categorical latent variable c on the covariates age94, male, and black:
Estimates S.E. Est./S.E.
C#1 ON
AGE94 -.285 .028 -10.045
MALE 2.578 .151 17.086
BLACK .158 .139 1.141
C#2 ON
AGE94 .069 .022 3.182
MALE .187 .110 1.702
BLACK -.606 .139 -4.357
C#3 ON
AGE94 -.317 .028 -11.311
MALE 1.459 .101 14.431
BLACK .999 .117 8.513
Intercepts
C#1 -1.822 .174 -10.485
C#2 -.748 .103 -7.258
C#3 -.324 .125 -2.600
Using (3), the log odds expression for a particular class compared to the last class is,
log odds = a + b1*age94 + b2*male + b3*black.
In the first example, the values of the three covariates are all zero so that only the intercepts contribute to the log odds. Probabilities are computed using (2). In the first step, the estimated intercept log odds values are exponentiated and summed. In the second step, each exponentiated value is divided by the sum to compute the probability for each class of c.
exp probability = exp/sum
log odds (c = 1) = -1.822 0.162 0.069
log odds (c = 2) = -0.748 0.473 0.201
log odds (c = 3) = -0.324 0.723 0.307
log odds (c = 4) = 0 1.0 0.424
_______ ________
sum 2.358 1.001
In the second example, the values of the three covariates are all one so that both the intercepts and the slopes contribute to the logs odds. In the first step, the log odds values for each class are computed. In the second step, the log odds values are exponentiated and summed. In the last step, the exponentiated value is divided by the sum to compute the probability for each class of c.
log odds (c = 1) = -1.822 + (-0.285*1) + (2.578*1) + (0.158*1)
= 0.629
log odds (c = 2) = -0.748 + 0.069*1 + 0.187*1 + (-0.606*1)
= -1.098
log odds (c = 3) = -0.324 + (-0.317*1) + 1.459*1 + 0.999*1
= 1.817
exp probability = exp/sum
log odds (c = 1) = 0.629 1.876 0.200
log odds (c = 2) = -1.098 0.334 0.036
log odds (c = 3) = 1.817 6.153 0.657
log odds (c = 4) = 0 1.0 0.107
_______ ________
sum 9.363 1.000
The interpretation of these probabilities is that individuals who have a value of 1 on each of the covariates have a probability of .200 of being in class 1, .036 of being in class 2, .657 of being in class 3, and .107 of being in class 4.
In the output shown above, the variable male has the value of 1 for males and 0 for females and the variable black has the value of 1 for blacks and 0 for non-blacks. The variable age94 has the value of 0 for age 16, 1 for age 17, up to 7 for age 23. An interpretation of the logistic regression coefficient for class 1 is that comparing class 1 to class 4, the log odds decreases by -.285 for a unit increase in age, is 2.578 higher for males than for females, and is .158 higher for blacks than for non-blacks. This implies that the odds ratio for being in class 1 versus class 4 when comparing males to females is 13.17 (exp 2.578), holding the other two covariates constant.
Following is a plot of the estimated probabilities in each of the four classes where age is plotted on the x-axis and the other covariates take on the value of one. This plot was created and exported as an EMF file using the PLOT command in conjunction with the Mplus post-processing graphics module.
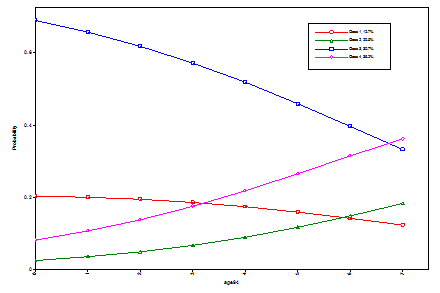
PARAMETERIZATION OF MODELS WITH MORE THAN ONE CATEGORICAL LATENT VARIABLE
The parameterization of models with more than one categorical latent variables is described in this section. There are three parameterizations available for these models. The first parameterization is based on a series of logistic regressions for non-recursive models. The second parameterization is that of loglinear modeling of frequency tables. The third parameterization uses probabilities rather than logits.
Following is a description of the logistic regression parameterization, specified using PARAMETERIZATION=LOGIT, for the following MODEL command for two categorical latent variables with three classes each:
MODEL:
%OVERALL%
c2#1 ON c1#1;
c2#1 ON c1#2;
c2#2 ON c1#1;
c2#2 ON c1#2;
The set of ON statements describes the logistic regression coefficients in the conditional distribution of c2 given c1. With three classes for both c2 and c1, there are a total of six parameters in this conditional distribution. Two of the parameters are intercepts for c2 and four are the logistic regression coefficients specified in the MODEL command.
For the c2 classes r = 1, 2, 3, the transition probabilities going from the classes of c1 to the classes of c2 are given by the following unordered multinomial logistic regression expressions:
P (c2 = r | c1 = 1) = exp (ar + br1) / sum1,
P (c2 = r | c1 = 2) = exp (ar + br2) / sum2,
P (c2 = r | c1 = 3) = exp (ar + br3) / sum3,
where a3 = 0, b31 = 0, b32 = 0, and b33 = 0 because the last class is the reference class, and sumj represents the sum of the exponentiations across the classes of c2 for c1 = j (j = 1, 2, 3). The corresponding log odds when comparing a c2 class to the last c2 class are summarized in the table below.
|
c2 |
||||
|
c1 |
|
1 |
2 |
3 |
|
1 |
a1 + b11 |
a2 + b21 |
0 |
|
|
2 |
a1 + b12 |
a2 + b22 |
0 |
|
|
3 |
a1 |
a2 |
0 |
|
The parameters in the table are referred to in the MODEL command using the following statements:
a1 [c2#1];
a2 [c2#2];
b11 c2#1 ON c1#1;
b12 c2#1 ON c1#2;
b21 c2#2 ON c1#1;
b22 c2#2 ON c1#2;
The TECH15 option is used in conjunction with TYPE=MIXTURE and PARAMETERIZATION=LOGIT to request marginal and conditional probabilities, including latent transition probabilities, for the categorical latent variables in a model. Conditional probabilities, including latent transition probabilities, for different values of a set of covariates can be computed using the LTA Calculator. It is accessed by choosing LTA calculator from the Mplus menu of the Mplus Editor. The logit parameterization with covariates is described in Muthén and Asparouhov (2011).
Following is a description of the loglinear parameterization for the following MODEL command for two categorical latent variables with three classes each:
MODEL:
%OVERALL%
c2#1 WITH c1#1;
c2#1 WITH c1#2;
c2#2 WITH c1#1;
c2#2 WITH c1#2;
The set of WITH statements describes the relationship between c1 and c2. The parameters in the table below are referred to in the MODEL command using the following statements:
a11 [c1#1];
a12 [c1#2];
a21 [c2#1];
a22 [c2#2];
w11 c2#1 WITH c1#1;
w12 c2#1 WITH c1#2;
w21 c2#2 WITH c1#1;
w22 c2#2 WITH c1#2;
The joint probabilities for the classes of c1 and c2 are computed using the multinomial logistic regression formula (2) in the previous section, summing over the nine cells shown in the table below.
|
c2 |
||||
|
c1 |
|
1 |
2 |
3 |
|
1 |
a11 + a21 + w11 |
a11 + a22 + w21 |
a11 |
|
|
2 |
a12 + a21 + w12 |
a12 + a22 + w22 |
a12 |
|
|
3 |
a21 |
a22 |
0 |
|
Following is a description of the probability parameterization for the following MODEL command for two categorical latent variables with three classes each:
MODEL:
%OVERALL%
c2#1 ON c1#1;
c2#1 ON c1#2;
c2#1 ON c1#3;
c2#2 ON c1#1;
c2#2 ON c1#2;
c2#2 ON c1#3;
The set of ON statements describes the probability parameters in the conditional distribution of c2 given c1. With three classes for both c2 and c1, there are a total of six probabilities in this conditional distribution. The last class of c2 is not referred to because the probabilities sum to one for each row, for example, the probability of being in class three of c2 for those in class 1 of c1 is 1 – (p11 + p12).
|
c2 |
||||
|
c1 |
|
1 |
2 |
3 |
|
1 |
p11 |
p12 |
- |
|
|
2 |
p21 |
p22 |
- |
|
|
3 |
p31 |
p32 |
- |
|
The marginal probabilities for c1 are referred to as:
[c1#1];
[c1#2];