CHAPTER 6
EXAMPLES: GROWTH MODELING, SURVIVAL ANALYSIS, AND N=1 TIME SERIES ANALYSIS
Growth models examine the development of individuals on one or more outcome variables over time. These outcome variables can be observed variables or continuous latent variables. Observed outcome variables can be continuous, censored, binary, ordered categorical (ordinal), counts, or combinations of these variable types if more than one growth process is being modeled. In growth modeling, random effects are used to capture individual differences in development. In a latent variable modeling framework, the random effects are reconceptualized as continuous latent variables, that is, growth factors.
Mplus takes a multivariate approach to growth modeling such that an outcome variable measured at four occasions gives rise to a four-variate outcome vector. In contrast, multilevel modeling typically takes a univariate approach to growth modeling where an outcome variable measured at four occasions gives rise to a single outcome for which observations at the different occasions are nested within individuals, resulting in two-level data. Due to the use of the multivariate approach, Mplus does not consider a growth model to be a two-level model as in multilevel modeling but a single-level model. With longitudinal data, the number of levels in Mplus is one less than the number of levels in conventional multilevel modeling. The multivariate approach allows flexible modeling of the outcomes such as differences in residual variances over time, correlated residuals over time, and regressions among the outcomes over time.
In Mplus, there are two options for handling the relationship between the outcome and time. One approach allows time scores to be parameters in the model so that the growth function can be estimated. This is the approach used in structural equation modeling. The second approach allows time to be a variable that reflects individually-varying times of observations. This variable has a random slope. This is the approach used in multilevel modeling. Random effects in the form of random slopes are also used to represent individual variation in the influence of time-varying covariates on outcomes.
Growth modeling in Mplus allows the analysis of multiple processes, both parallel and sequential; regressions among growth factors and random effects; growth modeling of factors measured by multiple indicators; and growth modeling as part of a larger latent variable model.
Survival modeling in Mplus includes both discrete-time and continuous-time analyses. Both types of analyses consider the time to an event. Discrete-time survival analysis is used when the outcome is recorded infrequently such as monthly or annually, typically leading to a limited number of measurements. Continuous-time survival analysis is used when the outcome is recorded more frequently such as hourly or daily, typically leading to a large number of measurements. Survival modeling is integrated into the general latent variable modeling framework so that it can be part of a larger model.
N=1 time series analysis is used to analyze intensive longitudinal data such as those obtained with ecological momentary assessments, experience sampling methods, daily diary methods, and ambulatory assessments for a single person. Such data typically have a large number of time points, for example, twenty to two hundred. The measurements are typically closely spaced in time. In Mplus, univariate autoregressive, regression, cross-lagged, confirmatory factor analysis, Item Response Theory, and structural equation models can be estimated for continuous, binary, ordered categorical (ordinal), or combinations of these variable types. Multilevel extensions of these models can be found in Chapter 9.
All growth and survival models can be estimated using the following special features:
· Single or multiple group analysis
· Missing data
· Complex survey data
· Latent variable interactions and non-linear factor analysis using maximum likelihood
· Random slopes
· Individually-varying times of observations
· Linear and non-linear parameter constraints
· Indirect effects including specific paths
· Maximum likelihood estimation for all outcome types
· Bootstrap standard errors and confidence intervals
· Wald chi-square test of parameter equalities
For continuous, censored with weighted least squares estimation, binary, and ordered categorical (ordinal) outcomes, multiple group analysis is specified by using the GROUPING option of the VARIABLE command for individual data or the NGROUPS option of the DATA command for summary data. For censored with maximum likelihood estimation, unordered categorical (nominal), and count outcomes, multiple group analysis is specified using the KNOWNCLASS option of the VARIABLE command in conjunction with the TYPE=MIXTURE option of the ANALYSIS command. The default is to estimate the model under missing data theory using all available data. The LISTWISE option of the DATA command can be used to delete all observations from the analysis that have missing values on one or more of the analysis variables. Corrections to the standard errors and chi-square test of model fit that take into account stratification, non-independence of observations, and unequal probability of selection are obtained by using the TYPE=COMPLEX option of the ANALYSIS command in conjunction with the STRATIFICATION, CLUSTER, and WEIGHT options of the VARIABLE command. The SUBPOPULATION option is used to select observations for an analysis when a subpopulation (domain) is analyzed. Latent variable interactions are specified by using the | symbol of the MODEL command in conjunction with the XWITH option of the MODEL command. Random slopes are specified by using the | symbol of the MODEL command in conjunction with the ON option of the MODEL command. Individually-varying times of observations are specified by using the | symbol of the MODEL command in conjunction with the AT option of the MODEL command and the TSCORES option of the VARIABLE command. Linear and non-linear parameter constraints are specified by using the MODEL CONSTRAINT command. Indirect effects are specified by using the MODEL INDIRECT command. Maximum likelihood estimation is specified by using the ESTIMATOR option of the ANALYSIS command. Bootstrap standard errors are obtained by using the BOOTSTRAP option of the ANALYSIS command. Bootstrap confidence intervals are obtained by using the BOOTSTRAP option of the ANALYSIS command in conjunction with the CINTERVAL option of the OUTPUT command. The MODEL TEST command is used to test linear restrictions on the parameters in the MODEL and MODEL CONSTRAINT commands using the Wald chi-square test.
Graphical displays of observed data and analysis results can be obtained using the PLOT command in conjunction with a post-processing graphics module. The PLOT command provides histograms, scatterplots, plots of individual observed and estimated values, and plots of sample and estimated means and proportions/probabilities. These are available for the total sample, by group, by class, and adjusted for covariates. The PLOT command includes a display showing a set of descriptive statistics for each variable. The graphical displays can be edited and exported as a DIB, EMF, or JPEG file. In addition, the data for each graphical display can be saved in an external file for use by another graphics program.
Following is the set of growth modeling examples included in this chapter:
· 6.1: Linear growth model for a continuous outcome
· 6.2: Linear growth model for a censored outcome using a censored model*
· 6.3: Linear growth model for a censored outcome using a censored-inflated model*
· 6.4: Linear growth model for a categorical outcome
· 6.5: Linear growth model for a categorical outcome using the Theta parameterization
· 6.6: Linear growth model for a count outcome using a Poisson model*
· 6.7: Linear growth model for a count outcome using a zero-inflated Poisson model*
· 6.8: Growth model for a continuous outcome with estimated time scores
· 6.9: Quadratic growth model for a continuous outcome
· 6.10: Linear growth model for a continuous outcome with time-invariant and time-varying covariates
· 6.11: Piecewise growth model for a continuous outcome
· 6.12: Growth model with individually-varying times of observation and a random slope for time-varying covariates for a continuous outcome
· 6.13: Growth model for two parallel processes for continuous outcomes with regressions among the random effects
· 6.14: Multiple indicator linear growth model for continuous outcomes
· 6.15: Multiple indicator linear growth model for categorical outcomes
· 6.16: Two-part (semicontinuous) growth model for a continuous outcome*
· 6.17: Linear growth model for a continuous outcome with first-order auto correlated residuals using non-linear constraints
· 6.18: Multiple group multiple cohort growth model
Following is the set of survival analysis examples included in this chapter:
· 6.19: Discrete-time survival analysis
· 6.20: Continuous-time survival analysis using the Cox regression model
· 6.21: Continuous-time survival analysis using a parametric proportional hazards model
· 6.22: Continuous-time survival analysis using a parametric proportional hazards model with a factor influencing survival*
Following is the set of N=1 time series analysis examples included in this chapter:
· 6.23: N=1 time series analysis with a univariate first-order autoregressive AR(1) model for a continuous dependent variable
· 6.24: N=1 time series analysis with a univariate first-order autoregressive AR(1) model for a continuous dependent variable with a covariate
· 6.25: N=1 time series analysis with a bivariate cross-lagged model for continuous dependent variables
· 6.26: N=1 time series analysis with a first-order autoregressive AR(1) confirmatory factor analysis (CFA) model with continuous factor indicators
· 6.27: N=1 time series analysis with a first-order autoregressive AR(1) IRT model with binary factor indicators
· 6.28: N=1 time series analysis with a bivariate cross-lagged model with two factors and continuous factor indicators
* Example uses numerical integration in the estimation of the model. This can be computationally demanding depending on the size of the problem.
TITLE: this is an example of a linear growth model for a continuous outcome
DATA: FILE IS ex6.1.dat;
VARIABLE: NAMES ARE y11-y14 x1 x2 x31-x34;
USEVARIABLES ARE y11-y14;
MODEL: i s | y11@0 y12@1 y13@2 y14@3;
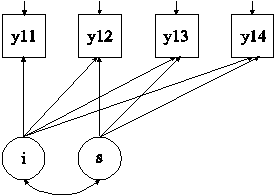
In this example, the linear growth model for a continuous outcome at four time points shown in the picture above is estimated.
TITLE: this is an example of a linear growth model for a continuous outcome
The TITLE command is used to provide a title for the analysis. The title is printed in the output just before the Summary of Analysis.
DATA: FILE IS ex6.1.dat;
The DATA command is used to provide information about the data set to be analyzed. The FILE option is used to specify the name of the file that contains the data to be analyzed, ex6.1.dat. Because the data set is in free format, the default, a FORMAT statement is not required.
VARIABLE: NAMES ARE y11-y14 x1 x2 x31-x34;
USEVARIABLES ARE y11-y14;
The VARIABLE command is used to provide information about the variables in the data set to be analyzed. The NAMES option is used to assign names to the variables in the data set. The data set in this example contains ten variables: y11, y12, y13, y14, x1, x2, x31, x32, x33, and x34. Note that the hyphen can be used as a convenience feature in order to generate a list of names. If not all of the variables in the data set are used in the analysis, the USEVARIABLES option can be used to select a subset of variables for analysis. Here the variables y11, y12, y13, and y14 have been selected for analysis. They represent the outcome measured at four equidistant occasions.
MODEL: i s | y11@0 y12@1 y13@2 y14@3;
The MODEL command is used to describe the model to be estimated. The | symbol is used to name and define the intercept and slope factors in a growth model. The names i and s on the left-hand side of the | symbol are the names of the intercept and slope growth factors, respectively. The statement on the right-hand side of the | symbol specifies the outcome and the time scores for the growth model. The time scores for the slope growth factor are fixed at 0, 1, 2, and 3 to define a linear growth model with equidistant time points. The zero time score for the slope growth factor at time point one defines the intercept growth factor as an initial status factor. The coefficients of the intercept growth factor are fixed at one as part of the growth model parameterization. The residual variances of the outcome variables are estimated and allowed to be different across time and the residuals are not correlated as the default.
In the parameterization of the growth model shown here, the intercepts of the outcome variables at the four time points are fixed at zero as the default. The means and variances of the growth factors are estimated as the default, and the growth factor covariance is estimated as the default because the growth factors are independent (exogenous) variables. The default estimator for this type of analysis is maximum likelihood. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator.
TITLE: this is an example of a linear growth model for a censored outcome using a censored model
DATA: FILE IS ex6.2.dat;
VARIABLE: NAMES ARE y11-y14 x1 x2 x31-x34;
USEVARIABLES ARE y11-y14;
CENSORED ARE y11-y14 (b);
ANALYSIS: ESTIMATOR = MLR;
MODEL: i s | y11@0 y12@1 y13@2 y14@3;
OUTPUT: TECH1 TECH8;
The difference between this example and Example 6.1 is that the outcome variable is a censored variable instead of a continuous variable. The CENSORED option is used to specify which dependent variables are treated as censored variables in the model and its estimation, whether they are censored from above or below, and whether a censored or censored-inflated model will be estimated. In the example above, y11, y12, y13, and y14 are censored variables. They represent the outcome variable measured at four equidistant occasions. The b in parentheses following y11-y14 indicates that y11, y12, y13, and y14 are censored from below, that is, have floor effects, and that the model is a censored regression model. The censoring limit is determined from the data. The residual variances of the outcome variables are estimated and allowed to be different across time and the residuals are not correlated as the default.
The default estimator for this type of analysis is a robust weighted least squares estimator. By specifying ESTIMATOR=MLR, maximum likelihood estimation with robust standard errors using a numerical integration algorithm is used. Note that numerical integration becomes increasingly more computationally demanding as the number of factors and the sample size increase. In this example, two dimensions of integration are used with a total of 225 integration points. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator.
In the parameterization of the growth model shown here, the intercepts of the outcome variables at the four time points are fixed at zero as the default. The means and variances of the growth factors are estimated as the default, and the growth factor covariance is estimated as the default because the growth factors are independent (exogenous) variables. The OUTPUT command is used to request additional output not included as the default. The TECH1 option is used to request the arrays containing parameter specifications and starting values for all free parameters in the model. The TECH8 option is used to request that the optimization history in estimating the model be printed in the output. TECH8 is printed to the screen during the computations as the default. TECH8 screen printing is useful for determining how long the analysis takes. An explanation of the other commands can be found in Example 6.1.
TITLE: this is an example of a linear growth model for a censored outcome using a censored-inflated model
DATA: FILE IS ex6.3.dat;
VARIABLE: NAMES ARE y11-y14 x1 x2 x31-x34;
USEVARIABLES ARE y11-y14;
CENSORED ARE y11-y14 (bi);
ANALYSIS: INTEGRATION = 7;
MODEL: i s | y11@0 y12@1 y13@2 y14@3;
ii si | y11#1@0 y12#1@1 y13#1@2 y14#1@3;
si@0;
OUTPUT: TECH1 TECH8;
The difference between this example and Example 6.1 is that the outcome variable is a censored variable instead of a continuous variable. The CENSORED option is used to specify which dependent variables are treated as censored variables in the model and its estimation, whether they are censored from above or below, and whether a censored or censored-inflated model will be estimated. In the example above, y11, y12, y13, and y14 are censored variables. They represent the outcome variable measured at four equidistant occasions. The bi in parentheses following y11-y14 indicates that y11, y12, y13, and y14 are censored from below, that is, have floor effects, and that a censored-inflated regression model will be estimated. The censoring limit is determined from the data. The residual variances of the outcome variables are estimated and allowed to be different across time and the residuals are not correlated as the default.
With a censored-inflated model, two growth models are estimated. The first | statement describes the growth model for the continuous part of the outcome for individuals who are able to assume values of the censoring point and above. The residual variances of the outcome variables are estimated and allowed to be different across time and the residuals are not correlated as the default. The second | statement describes the growth model for the inflation part of the outcome, the probability of being unable to assume any value except the censoring point. The binary latent inflation variable is referred to by adding to the name of the censored variable the number sign (#) followed by the number 1.
In the parameterization of the growth model for the continuous part of the outcome, the intercepts of the outcome variables at the four time points are fixed at zero as the default. The means and variances of the growth factors are estimated as the default, and the growth factor covariance is estimated as the default because the growth factors are independent (exogenous) variables.
In the parameterization of the growth model for the inflation part of the outcome, the intercepts of the outcome variable at the four time points are held equal as the default. The mean of the intercept growth factor is fixed at zero. The mean of the slope growth factor and the variances of the intercept and slope growth factors are estimated as the default, and the growth factor covariance is estimated as the default because the growth factors are independent (exogenous) variables.
In this example, the variance of the slope growth factor si for the inflation part of the outcome is fixed at zero. Because of this, the covariances among si and all of the other growth factors are fixed at zero as the default. The covariances among the remaining three growth factors are estimated as the default.
The default estimator for this type of analysis is maximum likelihood with robust standard errors using a numerical integration algorithm. Note that numerical integration becomes increasingly more computationally demanding as the number of factors and the sample size increase. In this example, three dimensions of integration are used with a total of 343 integration points. The INTEGRATION option of the ANALYSIS command is used to change the number of integration points per dimension from the default of 15 to 7. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. The OUTPUT command is used to request additional output not included as the default. The TECH1 option is used to request the arrays containing parameter specifications and starting values for all free parameters in the model. The TECH8 option is used to request that the optimization history in estimating the model be printed in the output. TECH8 is printed to the screen during the computations as the default. TECH8 screen printing is useful for determining how long the analysis takes. An explanation of the other commands can be found in Example 6.1.
TITLE: this is an example of a linear growth model for a categorical outcome
DATA: FILE IS ex6.4.dat;
VARIABLE: NAMES ARE u11-u14 x1 x2 x31-x34;
USEVARIABLES ARE u11-u14;
CATEGORICAL ARE u11-u14;
MODEL: i s | u11@0 u12@1 u13@2 u14@3;
The difference between this example and Example 6.1 is that the outcome variable is a binary or ordered categorical (ordinal) variable instead of a continuous variable. The CATEGORICAL option is used to specify which dependent variables are treated as binary or ordered categorical (ordinal) variables in the model and its estimation. In the example above, u11, u12, u13, and u14 are binary or ordered categorical variables. They represent the outcome variable measured at four equidistant occasions.
In the parameterization of the growth model shown here, the thresholds of the outcome variable at the four time points are held equal as the default. The mean of the intercept growth factor is fixed at zero. The mean of the slope growth factor and the variances of the intercept and slope growth factors are estimated as the default, and the growth factor covariance is estimated as the default because the growth factors are independent (exogenous) variables.
The default estimator for this type of analysis is a robust weighted least squares estimator. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. With the weighted least squares estimator, the probit model and the default Delta parameterization for categorical outcomes are used. The scale factor for the latent response variable of the categorical outcome at the first time point is fixed at one as the default, while the scale factors for the latent response variables at the other time points are free to be estimated. If a maximum likelihood estimator is used, the logistic model for categorical outcomes with a numerical integration algorithm is used (Hedeker & Gibbons, 1994). Note that numerical integration becomes increasingly more computationally demanding as the number of factors and the sample size increase. An explanation of the other commands can be found in Example 6.1.
TITLE: this is an example of a linear growth model for a categorical outcome using the Theta parameterization
DATA: FILE IS ex6.5.dat;
VARIABLE: NAMES ARE u11-u14 x1 x2 x31-x34;
USEVARIABLES ARE u11-u14;
CATEGORICAL ARE u11-u14;
ANALYSIS: PARAMETERIZATION = THETA;
MODEL: i s | u11@0 u12@1 u13@2 u14@3;
The difference between this example and Example 6.4 is that the Theta parameterization instead of the default Delta parameterization is used. In the Delta parameterization, scale factors for the latent response variables of the observed categorical outcomes are allowed to be parameters in the model, but residual variances for the latent response variables are not. In the Theta parameterization, residual variances for latent response variables are allowed to be parameters in the model, but scale factors are not. Because the Theta parameterization is used, the residual variance for the latent response variable at the first time point is fixed at one as the default, while the residual variances for the latent response variables at the other time points are free to be estimated. An explanation of the other commands can be found in Examples 6.1 and 6.4.
TITLE: this is an example of a linear growth model for a count outcome using a Poisson model
DATA: FILE IS ex6.6.dat;
VARIABLE: NAMES ARE u11-u14 x1 x2 x31-x34;
USEVARIABLES ARE u11-u14;
COUNT ARE u11-u14;
MODEL: i s | u11@0 u12@1 u13@2 u14@3;
OUTPUT: TECH1 TECH8;
The difference between this example and Example 6.1 is that the outcome variable is a count variable instead of a continuous variable. The COUNT option is used to specify which dependent variables are treated as count variables in the model and its estimation and whether a Poisson or zero-inflated Poisson model will be estimated. In the example above, u11, u12, u13, and u14 are count variables. They represent the outcome variable measured at four equidistant occasions.
In the parameterization of the growth model shown here, the intercepts of the outcome variables at the four time points are fixed at zero as the default. The means and variances of the growth factors are estimated as the default, and the growth factor covariance is estimated as the default because the growth factors are independent (exogenous) variables. The default estimator for this type of analysis is maximum likelihood with robust standard errors using a numerical integration algorithm. Note that numerical integration becomes increasingly more computationally demanding as the number of factors and the sample size increase. In this example, two dimensions of integration are used with a total of 225 integration points. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. The OUTPUT command is used to request additional output not included as the default. The TECH1 option is used to request the arrays containing parameter specifications and starting values for all free parameters in the model. The TECH8 option is used to request that the optimization history in estimating the model be printed in the output. TECH8 is printed to the screen during the computations as the default. TECH8 screen printing is useful for determining how long the analysis takes. An explanation of the other commands can be found in Example 6.1.
TITLE: this is an example of a linear growth model for a count outcome using a zero-inflated Poisson model
DATA: FILE IS ex6.7.dat;
VARIABLE: NAMES ARE u11-u14 x1 x2 x31-x34;
USEVARIABLES ARE u11-u14;
COUNT ARE u11-u14 (i);
ANALYSIS: INTEGRATION = 7;
MODEL: i s | u11@0 u12@1 u13@2 u14@3;
ii si | u11#1@0 u12#1@1 u13#1@2 u14#1@3;
s@0 si@0;
OUTPUT: TECH1 TECH8;
The difference between this example and Example 6.1 is that the outcome variable is a count variable instead of a continuous variable. The COUNT option is used to specify which dependent variables are treated as count variables in the model and its estimation and whether a Poisson or zero-inflated Poisson model will be estimated. In the example above, u11, u12, u13, and u14 are count variables. They represent the outcome variable u1 measured at four equidistant occasions. The i in parentheses following u11-u14 indicates that a zero-inflated Poisson model will be estimated.
With a zero-inflated Poisson model, two growth models are estimated. The first | statement describes the growth model for the count part of the outcome for individuals who are able to assume values of zero and above. The second | statement describes the growth model for the inflation part of the outcome, the probability of being unable to assume any value except zero. The binary latent inflation variable is referred to by adding to the name of the count variable the number sign (#) followed by the number 1.
In the parameterization of the growth model for the count part of the outcome, the intercepts of the outcome variables at the four time points are fixed at zero as the default. The means and variances of the growth factors are estimated as the default, and the growth factor covariance is estimated as the default because the growth factors are independent (exogenous) variables.
In the parameterization of the growth model for the inflation part of the outcome, the intercepts of the outcome variable at the four time points are held equal as the default. The mean of the intercept growth factor is fixed at zero. The mean of the slope growth factor and the variances of the intercept and slope growth factors are estimated as the default, and the growth factor covariance is estimated as the default because the growth factors are independent (exogenous) variables.
In this example, the variance of the slope growth factor s for the count part and the slope growth factor si for the inflation part of the outcome are fixed at zero. Because of this, the covariances among s, si, and the other growth factors are fixed at zero as the default. The covariance between the i and ii intercept growth factors is estimated as the default.
The default estimator for this type of analysis is maximum likelihood with robust standard errors using a numerical integration algorithm. Note that numerical integration becomes increasingly more computationally demanding as the number of factors and the sample size increase. In this example, two dimensions of integration are used with a total of 49 integration points. The INTEGRATION option of the ANALYSIS command is used to change the number of integration points per dimension from the default of 15 to 7. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. The OUTPUT command is used to request additional output not included as the default. The TECH1 option is used to request the arrays containing parameter specifications and starting values for all free parameters in the model. The TECH8 option is used to request that the optimization history in estimating the model be printed in the output. TECH8 is printed to the screen during the computations as the default. TECH8 screen printing is useful for determining how long the analysis takes. An explanation of the other commands can be found in Example 6.1.
TITLE: this is an example of a growth model for a continuous outcome with estimated time scores
DATA: FILE IS ex6.8.dat;
VARIABLE: NAMES ARE y11-y14 x1 x2 x31-x34;
USEVARIABLES ARE y11-y14;
MODEL: i s | y11@0 y12@1 y13*2 y14*3;
The difference between this example and Example 6.1 is that two of the time scores are estimated. The | statement highlighted above shows how to specify free time scores by using the asterisk (*) to designate a free parameter. Starting values are specified as the value following the asterisk (*). For purposes of model identification, two time scores must be fixed for a growth model with two growth factors. In the example above, the first two time scores are fixed at zero and one, respectively. The third and fourth time scores are free to be estimated at starting values of 2 and 3, respectively. The default estimator for this type of analysis is maximum likelihood. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. An explanation of the other commands can be found in Example 6.1.
TITLE: this is an example of a quadratic growth model for a continuous outcome
DATA: FILE IS ex6.9.dat;
VARIABLE: NAMES ARE y11-y14 x1 x2 x31-x34;
USEVARIABLES ARE y11-y14;
MODEL: i s q | y11@0 y12@1 y13@2 y14@3;
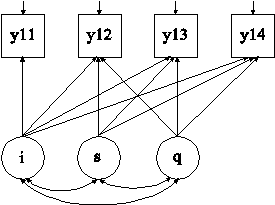
The difference between this example and Example 6.1 is that the quadratic growth model shown in the picture above is estimated. A quadratic growth model requires three random effects: an intercept factor (i), a linear slope factor (s), and a quadratic slope factor (q). The | symbol is used to name and define the intercept and slope factors in the growth model. The names i, s, and q on the left-hand side of the | symbol are the names of the intercept, linear slope, and quadratic slope factors, respectively. In the example above, the linear slope factor has equidistant time scores of 0, 1, 2, and 3. The time scores for the quadratic slope factor are the squared values of the linear time scores. These time scores are automatically computed by the program.
In the parameterization of the growth model shown here, the intercepts of the outcome variable at the four time points are fixed at zero as the default. The means and variances of the three growth factors are estimated as the default, and the three growth factors are correlated as the default because they are independent (exogenous) variables. The default estimator for this type of analysis is maximum likelihood. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. An explanation of the other commands can be found in Example 6.1.
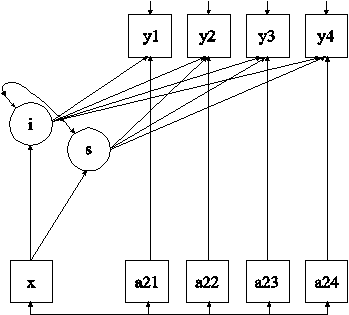
EXAMPLE 6.10: LINEAR GROWTH MODEL FOR A CONTINUOUS OUTCOME WITH TIME-INVARIANT AND TIME-VARYING COVARIATES
TITLE: this is an example of a linear growth model for a continuous outcome with time-invariant and time-varying covariates
DATA: FILE IS ex6.10.dat;
VARIABLE: NAMES ARE y11-y14 x1 x2 a31-a34;
MODEL: i s | y11@0 y12@1 y13@2 y14@3;
i s ON x1 x2;
y11 ON a31;
y12 ON a32;
y13 ON a33;
y14 ON a34;
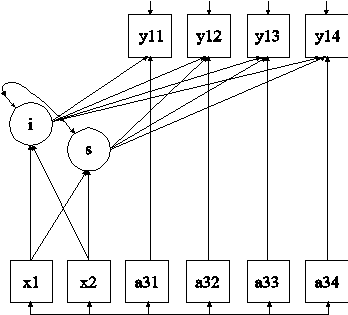
The difference between this example and Example 6.1 is that time-invariant and time-varying covariates as shown in the picture above are included in the model.
The first ON statement describes the linear regressions of the two growth factors on the time-invariant covariates x1 and x2. The next four ON statements describe the linear regressions of the outcome variable on the time-varying covariates a31, a32, a33, and a34 at each of the four time points. The default estimator for this type of analysis is maximum likelihood. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. An explanation of the other commands can be found in Example 6.1.
TITLE: this is an example of a piecewise growth model for a continuous outcome
DATA: FILE IS ex6.11.dat;
VARIABLE: NAMES ARE y1-y5;
MODEL: i s1 | y1@0 y2@1 y3@2 y4@2 y5@2;
i s2 | y1@0 y2@0 y3@0 y4@1 y5@2;
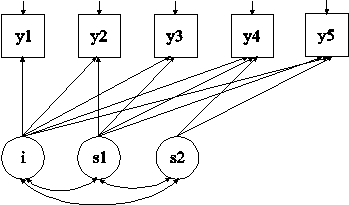
In this example, the piecewise growth model shown in the picture above is estimated. In a piecewise growth model, different phases of development are captured by more than one slope growth factor. The first | statement specifies a linear growth model for the first phase of development which includes the first three time points. The second | statement specifies a linear growth model for the second phase of development which includes the last three time points. Note that there is one intercept growth factor i. It must be named in the specification of both growth models when using the | symbol.
In the parameterization of the growth models shown here, the intercepts of the outcome variable at the five time points are fixed at zero as the default. The means and variances of the three growth factors are estimated as the default, and the three growth factors are correlated as the default because they are independent (exogenous) variables. The default estimator for this type of analysis is maximum likelihood. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. An explanation of the other commands can be found in Example 6.1.
TITLE: this is an example of a growth model with individually-varying times of observation and a random slope for time-varying covariates for a continuous outcome
DATA: FILE IS ex6.12.dat;
VARIABLE: NAMES ARE y1-y4 x a11-a14 a21-a24;
TSCORES = a11-a14;
ANALYSIS: TYPE = RANDOM;
MODEL: i s | y1-y4 AT a11-a14;
st | y1 ON a21;
st | y2 ON a22;
st | y3 ON a23;
st | y4 ON a24;
i s st ON x;
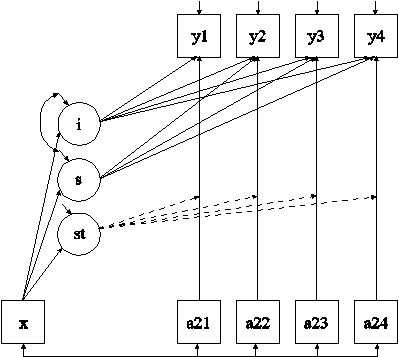
In this example, the growth model with individually-varying times of observation, a time-invariant covariate, and time-varying covariates with random slopes shown in the picture above is estimated. The st shown in a circle represents the random slope. The broken arrows from st to the arrows from a21 to y1, a22 to y2, a23 to y3, and a24 to y4 indicate that the slopes in these regressions are random.
The TSCORES option is used to identify the variables in the data set that contain information about individually-varying times of observation for the outcomes. The TYPE option is used to describe the type of analysis that is to be performed. By selecting RANDOM, a growth model with random slopes will be estimated.
The | symbol is used in conjunction with TYPE=RANDOM to name and define the random effect variables in the model. The names on the left-hand side of the | symbol name the random effect variables. In the first | statement, the AT option is used on the right-hand side of the | symbol to define a growth model with individually-varying times of observation for the outcome variable. Two growth factors are used in the model, a random intercept, i, and a random slope, s.
In the parameterization of the growth model shown here, the intercepts of the outcome variables are fixed at zero as the default. The residual variances of the outcome variables are free to be estimated as the default. The residual covariances of the outcome variables are fixed at zero as the default. The means, variances, and covariances of the intercept and slope growth factors are free as the default.
The second, third, fourth, and fifth | statements use the ON option to name and define the random slope variables in the model. The name on the left-hand side of the | symbol names the random slope variable. The statement on the right-hand side of the | symbol defines the random slope variable. In the second | statement, the random slope st is defined by the linear regression of the dependent variable y1 on the time-varying covariate a21. In the third | statement, the random slope st is defined by the linear regression of the dependent variable y2 on the time-varying covariate a22. In the fourth | statement, the random slope st is defined by the linear regression of the dependent variable y3 on the time-varying covariate a23. In the fifth | statement, the random slope st is defined by the linear regression of the dependent variable y4 on the time-varying covariate a24. Random slopes with the same name are treated as one variable during model estimation. The ON statement describes the linear regressions of the intercept growth factor i, the slope growth factor s, and the random slope st on the covariate x. The intercepts and residual variances of, i, s, and st, are free as the default. The residual covariance between i and s is estimated as the default. The residual covariances between st and i and s are fixed at zero as the default. The default estimator for this type of analysis is maximum likelihood with robust standard errors. The estimator option of the ANALYSIS command can be used to select a different estimator. An explanation of the other commands can be found in Example 6.1.
EXAMPLE 6.13: GROWTH MODEL FOR TWO PARALLEL PROCESSES FOR CONTINUOUS OUTCOMES WITH REGRESSIONS AMONG THE RANDOM EFFECTS
TITLE: this is an example of a growth model for two parallel processes for continuous
outcomes with regressions among the random effects
DATA: FILE IS ex6.13.dat;
VARIABLE: NAMES ARE y11 y12 y13 y14 y21 y22 y23 y24;
MODEL: i1 s1 | y11@0 y12@1 y13@2 y14@3;
i2 s2 | y21@0 y22@1 y23@2 y24@3;
s1 ON i2;
s2 ON i1;
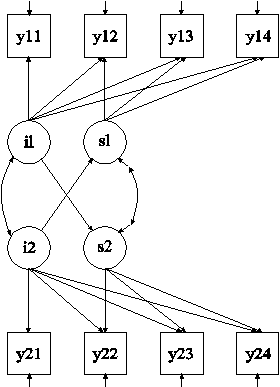
In this example, the model for two parallel processes shown in the picture above is estimated. Regressions among the growth factors are included in the model.
The | statements are used to name and define the intercept and slope growth factors for the two linear growth models. The names i1 and s1 on the left-hand side of the first | statement are the names of the intercept and slope growth factors for the first linear growth model. The names i2 and s2 on the left-hand side of the second | statement are the names of the intercept and slope growth factors for the second linear growth model. The values on the right-hand side of the two | statements are the time scores for the two slope growth factors. For both growth models, the time scores of the slope growth factors are fixed at 0, 1, 2, and 3 to define a linear growth model with equidistant time points. The zero time score for the slope growth factor at time point one defines the intercept factors as initial status factors. The coefficients of the intercept growth factors are fixed at one as part of the growth model parameterization. The residual variances of the outcome variables are estimated and allowed to be different across time, and the residuals are not correlated as the default.
In the parameterization of the growth model shown here, the intercepts of the outcome variables at the four time points are fixed at zero as the default. The means and variances of the intercept growth factors are estimated as the default, and the intercept growth factor covariance is estimated as the default because the intercept growth factors are independent (exogenous) variables. The intercepts and residual variances of the slope growth factors are estimated as the default, and the slope growth factors are correlated as the default because residuals are correlated for latent variables that do not influence any other variable in the model except their own indicators.
The two ON statements describe the regressions of the slope growth factor for each process on the intercept growth factor of the other process. The default estimator for this type of analysis is maximum likelihood. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. An explanation of the other commands can be found in Example 6.1.
TITLE: this is an example of a multiple indicator linear growth model for continuous outcomes
DATA: FILE IS ex6.14.dat;
VARIABLE: NAMES ARE y11 y21 y31 y12 y22 y32 y13
y23 y33;
MODEL: f1 BY y11
y21-y31 (1-2);
f2 BY y12
y22-y32 (1-2);
f3 BY y13
y23-y33 (1-2);
[y11 y12 y13] (3);
[y21 y22 y23] (4);
[y31 y32 y33] (5);
i s | f1@0 f2@1 f3@2;
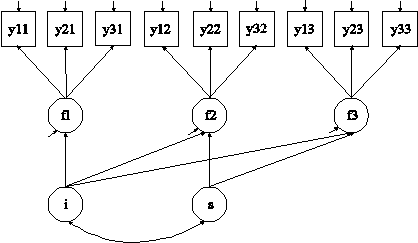
In this example, the multiple indicator linear growth model for continuous outcomes shown in the picture above is estimated. The first BY statement specifies that f1 is measured by y11, y21, and y31. The second BY statement specifies that f2 is measured by y12, y22, and y32. The third BY statement specifies that f3 is measured by y13, y23, and y33. The metric of the three factors is set automatically by the program by fixing the first factor loading in each BY statement to one. This option can be overridden. The residual variances of the factor indicators are estimated and the residuals are not correlated as the default.
A multiple indicator growth model requires measurement invariance of the three factors across time. Measurement invariance is specified by holding the intercepts and factor loadings of the factor indicators equal over time. The (1-2) following the factor loadings in the three BY statements uses the list function to assign equality labels to these parameters. The label 1 is assigned to the factor loadings of y21, y22, and y23 which holds these factor loadings equal across time. The label 2 is assigned to the factor loadings of y31, y32, and y33 which holds these factor loadings equal across time. The factor loadings of y11, y21, and y31 are fixed at one as described above. The bracket statements refer to the intercepts. The (3) holds the intercepts of y11, y12, and y13 equal. The (4) holds the intercepts of y21, y22, and y23 equal. The (5) holds the intercepts of y31, y32, and y33 equal.
The | statement is used to name and define the intercept and slope factors in the growth model. The names i and s on the left-hand side of the | are the names of the intercept and slope growth factors, respectively. The values on the right-hand side of the | are the time scores for the slope growth factor. The time scores of the slope growth factor are fixed at 0, 1, and 2 to define a linear growth model with equidistant time points. The zero time score for the slope growth factor at time point one defines the intercept growth factor as an initial status factor. The coefficients of the intercept growth factor are fixed at one as part of the growth model parameterization. The residual variances of the factors f1, f2, and f3 are estimated and allowed to be different across time, and the residuals are not correlated as the default.
In the parameterization of the growth model shown here, the intercepts of the factors f1, f2, and f3 are fixed at zero as the default. The mean of the intercept growth factor is fixed at zero and the mean of the slope growth factor is estimated as the default. The variances of the growth factors are estimated as the default, and the growth factors are correlated as the default because they are independent (exogenous) variables. The default estimator for this type of analysis is maximum likelihood. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. An explanation of the other commands can be found in Example 6.1.
TITLE: this is an example of a multiple indicator linear growth model for categorical outcomes
DATA: FILE IS ex6.15.dat;
VARIABLE: NAMES ARE u11 u21 u31 u12 u22 u32
u13 u23 u33;
CATEGORICAL ARE u11 u21 u31 u12 u22 u32 u13 u23 u33;
MODEL: f1 BY u11
u21-u31 (1-2);
f2 BY u12
u22-u32 (1-2);
f3 BY u13
u23-u33 (1-2);
[u11$1 u12$1 u13$1] (3);
[u21$1 u22$1 u23$1] (4);
[u31$1 u32$1 u33$1] (5);
{u11-u31@1 u12-u33};
i s | f1@0 f2@1 f3@2;
The difference between this example and Example 6.14 is that the factor indicators are binary or ordered categorical (ordinal) variables instead of continuous variables. The CATEGORICAL option is used to specify which dependent variables are treated as binary or ordered categorical (ordinal) variables in the model and its estimation. In the example above, all of the factor indicators are categorical variables. The program determines the number of categories for each indicator.
For binary and ordered categorical factor indicators, thresholds are modeled rather than intercepts or means. The number of thresholds for a categorical variable is equal to the number of categories minus one. In the example above, the categorical variables are binary so they have one threshold. Thresholds are referred to by adding to the variable name a $ followed by a number. The thresholds of the factor indicators are referred to as u11$1, u12$1, u13$1, u21$1, u22$1, u23$1, u31$1, u32$1, and u33$1. Thresholds are referred to in square brackets.
The growth model requires measurement invariance of the three factors across time. Measurement invariance is specified by holding the thresholds and factor loadings of the factor indicators equal over time. The (3) after the first bracket statement holds the thresholds of u11, u12, and u13 equal. The (4) after the second bracket statement holds the thresholds of u21, u22, and u23 equal. The (5) after the third bracket statement holds the thresholds of u31, u32, and u33 equal. A list of observed variables in curly brackets refers to scale factors. These are part of the model with weighted least squares estimation and the Delta parameterization. The scale factors for the latent response variables of the categorical outcomes for the first factor are fixed at one, while the scale factors for the latent response variables for the other factors are free to be estimated. An explanation of the other commands can be found in Examples 6.1 and 6.14.
TITLE: this is an example of a two-part (semicontinuous) growth model for a continuous outcome
DATA: FILE = ex6.16.dat;
DATA TWOPART:
NAMES = y1-y4;
BINARY = bin1-bin4;
CONTINUOUS = cont1-cont4;
VARIABLE: NAMES = x y1-y4;
USEVARIABLES = bin1-bin4 cont1-cont4;
CATEGORICAL = bin1-bin4;
MISSING = ALL(999);
ANALYSIS: ESTIMATOR = MLR;
MODEL: iu su | bin1@0 bin2@1 bin3@2 bin4@3;
iy sy | cont1@0 cont2@1 cont3@2 cont4@3;
su@0; iu WITH sy@0;
OUTPUT: TECH1 TECH8;
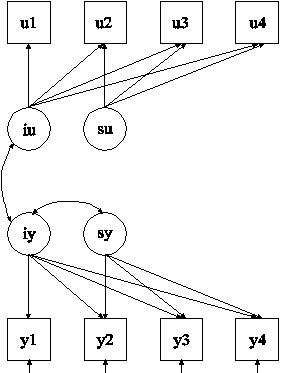
In this example, the two-part (semicontinuous) growth model (Olsen & Schafer, 2001) for a continuous outcome shown in the picture above is estimated. This is one type of model that can be considered when a variable has a floor effect, for example, a preponderance of zeroes. The analysis requires that one binary variable and one continuous variable be created from the outcome being studied.
The DATA TWOPART command is used to create a binary and a continuous variable from a variable with a floor effect. In this example, a set of binary and continuous variables are created using the default value of zero as the cutpoint. The CUTPOINT option of the DATA TWOPART command can be used to select another value. The two variables are created using the following rules:
1. If the value of the original variable is missing, both the new binary and the new continuous variable values are missing.
2. If the value of the original variable is greater than the cutpoint value, the new binary variable value is one and the new continuous variable value is the log of the original variable as the default.
3. If the value of the original variable is less than or equal to the cutpoint value, the new binary variable value is zero and the new continuous variable value is missing.
The TRANSFORM option of the DATA TWOPART command can be used to select an alternative to the default log transformation of the new continuous variables. One choice is no transformation.
The NAMES option of the DATA TWOPART command is used to identify the variables from the NAMES option of the VARIABLE command that are used to create a set of binary and continuous variables. Variables y1, y2, y3, and y4 are used. The BINARY option is used to assign names to the new set of binary variables. The names for the new binary variables are bin1, bin2, bin3, and bin4. The CONTINUOUS option is used to assign names to the new set of continuous variables. The names for the new continuous variables are cont1, cont2, cont3, and cont4. The new variables must be placed on the USEVARIABLES statement of the VARIABLE command if they are used in the analysis.
The CATEGORICAL option is used to specify which dependent variables are treated as binary or ordered categorical (ordinal) variables in the model and its estimation. In the example above, bin1, bin2, bin3, and bin4 are binary variables. The MISSING option is used to identify the values or symbols in the analysis data set that are to be treated as missing or invalid. In this example, the number 999 is the missing value flag. The default is to estimate the model under missing data theory using all available data. By specifying ESTIMATOR=MLR, a maximum likelihood estimator with robust standard errors using a numerical integration algorithm will be used. Note that numerical integration becomes increasingly more computationally demanding as the number of growth factors and the sample size increase. In this example, one dimension of integration is used with a total of 15 integration points. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator.
The first | statement specifies a linear growth model for the binary outcome. The second | statement specifies a linear growth model for the continuous outcome. In the parameterization of the growth model for the binary outcome, the thresholds of the outcome variable at the four time points are held equal as the default. The mean of the intercept growth factor is fixed at zero. The mean of the slope growth factor and the variances of the intercept and slope growth factors are estimated as the default. In this example, the variance of the slope growth factor is fized at zero for simplicity. In the parameterization of the growth model for the continuous outcome, the intercepts of the outcome variables at the four time points are fixed at zero as the default. The means and variances of the growth factors are estimated as the default, and the growth factors are correlated as the default because they are independent (exogenous) variables.
It is often the case that not all growth factor covariances are significant in two-part growth modeling. Fixing these at zero stabilizes the estimation. This is why the growth factor covariance between iu and sy is fixed at zero. The OUTPUT command is used to request additional output not included as the default. The TECH1 option is used to request the arrays containing parameter specifications and starting values for all free parameters in the model. The TECH8 option is used to request that the optimization history in estimating the model be printed in the output. TECH8 is printed to the screen during the computations as the default. TECH8 screen printing is useful for determining how long the analysis takes. An explanation of the other commands can be found in Example 6.1.
TITLE: this is an example of a linear growth model for a continuous outcome with first-order auto correlated residuals using non-linear constraints
DATA: FILE = ex6.17.dat;
VARIABLE: NAMES = y1-y4;
MODEL: i s | y1@0 y2@1 y3@2 y4@3;
y1-y4 (resvar);
y1-y3 PWITH y2-y4 (p1);
y1-y2 PWITH y3-y4 (p2);
y1 WITH y4 (p3);
MODEL CONSTRAINT:
NEW (corr);
p1 = resvar*corr;
p2 = resvar*corr**2;
p3 = resvar*corr**3;
The difference between this example and Example 6.1 is that first-order auto correlated residuals have been added to the model. In a model with first-order correlated residuals, one residual variance parameter and one residual auto-correlation parameter are estimated.
In the MODEL command, the label resvar following the residual variances serves two purposes. It specifies that the residual variances are held equal to each other and gives that residual variance parameter a label to be used in the MODEL CONSTRAINT command. The labels p1, p2, and p3 specify that the residual covariances at adjacent time points, at adjacent time points once removed, and at adjacent time points twice removed are held equal. The MODEL CONSTRAINT command is used to define linear and non-linear constraints on the parameters in the model. In the MODEL CONSTRAINT command, the NEW option is used to introduce a new parameter that is not part of the MODEL command. This residual auto-correlation parameter is referred to as corr. The p1 parameter constraint specifies that the residual covariances at adjacent time points are equal to the residual variance parameter multiplied by the auto-correlation parameter. The p2 parameter constraint specifies that the residual covariances at adjacent time points once removed are equal to the residual variance parameter multiplied by the auto-correlation parameter to the power of two. The p3 parameter constraint specifies that the residual covariance at adjacent time points twice removed is equal to the residual variance parameter multiplied by the auto-correlation parameter to the power of three. An explanation of the other commands can be found in Example 6.1.
TITLE: this is an example of a multiple group
multiple cohort growth model
DATA: FILE = ex6.18.dat;
VARIABLE: NAMES = y1-y4 x a21-a24 g;
GROUPING = g (1 = 1990 2 = 1989 3 = 1988);
MODEL: i s |y1@0 y2@.2 y3@.4 y4@.6;
[i] (1); [s] (2);
i (3); s (4);
i WITH s (5);
i ON x (6);
s ON x (7);
y1 ON a21;
y2 ON a22 (12);
y3 ON a23 (14);
y4 ON a24 (16);
y2-y4 (22-24);
MODEL 1989:
i s |y1@.1 y2@.3 y3@.5 y4@.7;
y1 ON a21;
y2 ON a22;
y3 ON a23;
y4 ON a24;
y1-y4;
MODEL 1988:
i s |y1@.2 y2@.4 y3@.6 y4@.8;
y1 ON a21 (12);
y2 ON a22 (14);
y3 ON a23 (16);
y4 ON a24;
y1-y3 (22-24);
y4;
OUTPUT: TECH1 MODINDICES(3.84);
In this example, the multiple group multiple cohort growth model shown in the picture above is estimated. Longitudinal research studies often collect data on several different groups of individuals defined by their birth year or cohort. This allows the study of development over a wider age range than the length of the study and is referred to as an accelerated or sequential cohort design. The interest in these studies is the development of an outcome over age not measurement occasion. This can be handled by rearranging the data so that age is the time axis using the DATA COHORT command or using a multiple group approach as described in this example. The advantage of the multiple group approach is that it can be used to test assumptions of invariance of growth parameters across cohorts.
In the multiple group approach the variables in the data set represent the measurement occasions. In this example, there are four measurement occasions: 2000, 2002, 2004, and 2006. Therefore there are four variables to represent the outcome. In this example, there are three cohorts with birth years 1988, 1989, and 1990. It is the combination of the time of measurement and birth year that determines the ages represented in the data. This is shown in the table below where rows represent cohort and columns represent measurement occasion. The entries in the table represent the ages. In this example, ages 10 to 18 are represented.
|
M.O./ Cohort |
2000 |
2002 |
2004 |
2006 |
|
1988 |
12 |
14 |
16 |
18 |
|
1989 |
11 |
13 |
15 |
17 |
|
1990 |
10 |
12 |
14 |
16 |
The model that is estimated uses the time axis of age as shown in the table below where rows represent cohort and columns represent age. The entries for the first three rows in the table are the years of the measurement occasions. The entries for the last row are the time scores for a linear model.
|
Age/ Cohort |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
|
1988 |
|
|
2000 |
|
2002 |
|
2004 |
|
2006 |
|
1989 |
|
2000 |
|
2002 |
|
2004 |
|
2006 |
|
|
1990 |
2000 |
|
2002 |
|
2004 |
|
2006 |
|
|
|
Time Score |
0 |
.1 |
.2 |
.3 |
.4 |
.5 |
.6 |
.7 |
.8 |
As shown in the table, three ages are represented by more than one cohort. Age 12 is represented by cohorts 1988 and 1990 measured in 2000 and 2002; age 14 is represented by cohorts 1988 and 1990 measured in 2002 and 2004; and age 16 is represented by cohorts 1988 and 1990 measured in 2004 and 2006. This information is needed to constrain parameters to be equal in the multiple group model.
The table also provides information about the time scores for each cohort. The time scores are obtained as the difference in age between measurement occasions divided by ten. The division is used to avoid large time scores which can lead to convergence problems. Cohort 1990 provides information for ages 10, 12, 14, and 16. The time scores for cohort 2000 are 0, .2, .4, and .6. Cohort 1989 provides information for ages 11, 13, 15, and 17. The time scores for cohort 1989 are .1, .3, .5, and .7. Cohort 1988 provides information for ages 12, 14, 16, and 18. The time scores for cohort 1988 are .2, .4, .6, and .8.
The GROUPING option is used to identify the variable in the data set that contains information on group membership when the data for all groups are stored in a single data set. The information in parentheses after the grouping variable name assigns labels to the values of the grouping variable found in the data set. In the example above, observations with g equal to 1 will be assigned the label 1990, individuals with g equal to 2 will be assigned the label 1989, and individuals with g equal to 3 will be assigned the label 1988. These labels are used in conjunction with the MODEL command to specify model statements specific to each group.
In multiple group analysis, two variations of the MODEL command are used. They are MODEL and MODEL followed by a label. MODEL describes the overall model to be estimated for each group. MODEL followed by a label describes differences between the overall model and the model for the group designated by the label. In the MODEL command, the | symbol is used to name and define the intercept and slope factors in a growth model. The names i and s on the left-hand side of the | symbol are the names of the intercept and slope growth factors, respectively. The statement on the right-hand side of the | symbol specifies the outcome and the time scores for the growth model. The time scores for the slope growth factor are fixed at 0, .2, .4, and .6. These are the time scores for cohort 1990. The zero time score for the slope growth factor at time point one defines the intercept growth factor as an initial status factor for age 10. The coefficients of the intercept growth factor are fixed at one as part of the growth model parameterization. The residual variances of the outcome variables are estimated and allowed to be different across age and the residuals are not correlated as the default. The time scores for the other two cohorts are specified in the group-specific MODEL commands. The group-specific MODEL command for cohort 1989 fixes the time scores at .1, .3, .5, and .7. The group-specific MODEL command for cohort 1988 fixes the time scores at .2, .4, .6, and .8.
The equalities specified by the numbers in parentheses represent the baseline assumption that the cohorts come from the same population. Equalities specified in the overall MODEL command constrain parameters to be equal across all groups. All parameters related to the growth factors are constrained to be equal across all groups. Other parameters are held equal when an age is represented by more than one cohort. For example, the ON statement with the (12) equality in the overall MODEL command describes the linear regression of y2 on the time-varying covariate a22 for cohort 1990 at age 12. In the group-specific MODEL command for cohort 1988, the ON statement with the (12) equality describes the linear regression of y1 on the time-varying covariate a21 for cohort 1988 at age 12. Other combinations of cohort and age do not involve equality constraints. Cohort 1990 is the only cohort that represents age 10; cohort 1989 is the only cohort that represents ages 11, 13, 15, 17; and cohort 1988 is the only cohort that represents age 18. Statements in the group-specific MODEL commands relax equality constraints specified in the overall MODEL command. An explanation of the other commands can be found in Example 6.1.
TITLE: this is an example of a discrete-time survival analysis
DATA: FILE IS ex6.19.dat;
VARIABLE: NAMES ARE u1-u4 x;
CATEGORICAL = u1-u4;
MISSING = ALL (999);
ANALYSIS: ESTIMATOR = MLR;
MODEL: f BY u1-u4@1;
f ON x;
f@0;

In this example, the discrete-time survival analysis model shown in the picture above is estimated. Each u variable represents whether or not a single non-repeatable event has occurred in a specific time period. The value 1 means that the event has occurred, 0 means that the event has not occurred, and a missing value flag means that the event has occurred in a preceding time period or that the individual has dropped out of the study (Muthén & Masyn, 2005). The factor f is used to specify a proportional odds assumption for the hazards of the event.
The MISSING option is used to identify the values or symbols in the analysis data set that are to be treated as missing or invalid. In this example, the number 999 is the missing value flag. The default is to estimate the model under missing data theory using all available data. The default estimator for this type of analysis is a robust weighted least squares estimator. By specifying ESTIMATOR=MLR, maximum likelihood estimation with robust standard errors is used. The BY statement specifies that f is measured by u1, u2, u3, and u4 where the factor loadings are fixed at one. This represents a proportional odds assumption where the covariate x has the same influence on u1, u2, u3, and u4. The ON statement describes the linear regression of f on the covariate x. The residual variance of f is fixed at zero to correspond to a conventional discrete-time survival model. An explanation of the other commands can be found in Example 6.1.
TITLE: this is an example of a continuous-time
survival analysis using the Cox regression model
DATA: FILE = ex6.20.dat;
VARIABLE: NAMES = t x tc;
SURVIVAL = t;
TIMECENSORED = tc (0 = NOT 1 = RIGHT);
MODEL: t ON x;
![]()
In this example, the continuous-time survival analysis model shown in the picture above is estimated. This is the Cox regression model (Singer & Willett, 2003). The profile likelihood method is used for model estimation (Asparouhov et al., 2006).
The SURVIVAL option is used to identify the variables that contain information about time to event and to provide information about the number and lengths of the time intervals in the baseline hazard function to be used in the analysis. The SURVIVAL option must be used in conjunction with the TIMECENSORED option. In this example, t is the variable that contains time-to-event information. Because nothing is specified in parentheses behind t, the default baseline hazard function is used. The TIMECENSORED option is used to identify the variables that contain information about right censoring. In this example, the variable is named tc. The information in parentheses specifies that the value zero represents no censoring and the value one represents right censoring. This is the default.
In the MODEL command, the ON statement describes the loglinear regression of the time-to-event variable t on the covariate x. The default estimator for this type of analysis is maximum likelihood with robust standard errors. The estimator option of the ANALYSIS command can be used to select a different estimator. An explanation of the other commands can be found in Example 6.1.
TITLE: this is an example of a continuous-time
survival analysis using a parametric proportional hazards model
DATA: FILE = ex6.21.dat;
VARIABLE: NAMES = t x tc;
SURVIVAL = t(20*1);
TIMECENSORED = tc (0 = NOT 1 = RIGHT);
ANALYSIS: BASEHAZARD = ON;
MODEL: [t#1-t#21];
t ON x;
The difference between this example and Example 6.20 is that a parametric proportional hazards model is used instead of a Cox regression model. In contrast to the Cox regression model, the parametric model estimates parameters and their standard errors for the baseline hazard function (Asparouhov et al., 2006).
The SURVIVAL option is used to identify the variables that contain information about time to event and to provide information about the number and lengths of the time intervals in the baseline hazard function to be used in the analysis. The SURVIVAL option must be used in conjunction with the TIMECENSORED option. In this example, t is the variable that contains time-to-event information. The numbers in parentheses following the time-to-event variable specify that twenty time intervals of length one are used in the analysis for the baseline hazard function. The TIMECENSORED option is used to identify the variables that contain information about right censoring. In this example, this variable is named tc. The information in parentheses specifies that the value zero represents no censoring and the value one represents right censoring. This is the default.
The BASEHAZARD option of the ANALYSIS command is used with continuous-time survival analysis to specify whether the baseline hazard parameters are treated as model parameters or as auxiliary parameters. The ON setting specifies that the parameters are treated as model parameters. There are as many baseline hazard parameters as there are time intervals plus one. These parameters can be referred to in the MODEL command by adding to the name of the time-to-event variable the number sign (#) followed by a number. In the MODEL command, the bracket statement specifies that the 21 baseline hazard parameters are part of the model.
The default estimator for this type of analysis is maximum likelihood with robust standard errors. The estimator option of the ANALYSIS command can be used to select a different estimator. An explanation of the other commands can be found in Examples 6.1 and 6.20.
TITLE: this is an example of a continuous-time
survival analysis using a parametric proportional hazards model with a factor influencing survival
DATA: FILE = ex6.22.dat;
VARIABLE: NAMES = t u1-u4 x tc;
SURVIVAL = t (20*1);
TIMECENSORED = tc;
CATEGORICAL = u1-u4;
ANALYSIS: ALGORITHM = INTEGRATION;
BASEHAZARD = ON;
MODEL: f BY u1-u4;
[t#1-t#21];
t ON x f;
f ON x;
OUTPUT: TECH1 TECH8;
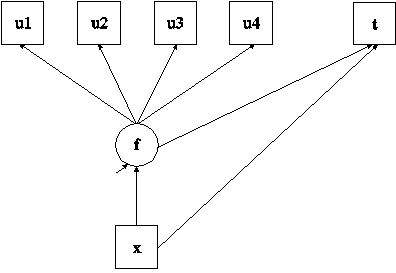
In this example, the continuous-time survival analysis model shown in the picture above is estimated. The model is similar to Larsen (2005) although in this example the analysis uses a parametric baseline hazard function (Asparouhov et al., 2006).
By specifying ALGORITHM=INTEGRATION, a maximum likelihood estimator with robust standard errors using a numerical integration algorithm will be used. Note that numerical integration becomes increasingly more computationally demanding as the number of factors and the sample size increase. In this example, one dimension of integration is used with a total of 15 integration points. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator.
In the MODEL command the BY statement specifies that f is measured by the binary indicators u1, u2, u3, and u4. The bracket statement specifies that the 21 baseline hazard parameters are part of the model. The first ON statement describes the loglinear regression of the time-to-event variable t on the covariate x and the factor f. The second ON statement describes the linear regression of f on the covariate x. An explanation of the other commands can be found in Examples 6.1 and 6.21.
TITLE: this is an example of an N=1 time series analysis with a univariate first-order autoregressive AR(1) model for a continuous dependent variable
DATA: FILE = ex6.23.dat;
VARIABLE: NAMES = y;
LAGGED = y(1);
ANALYSIS: ESTIMATOR = BAYES;
PROCESSORS = 2;
BITERATIONS = (2000);
MODEL: y ON y&1;
OUTPUT: TECH1 TECH8;
PLOT: TYPE = PLOT3;

In this example, the N=1 time series analysis with a univariate first-order autoregressive AR(1) model for a continuous dependent variable shown in the picture above is estimated (Shumway & Stoffer, 2011). The subscript t refers to a time point and the subscript t-1 refers to the previous time point. The dots indicate that the process includes both previous and future time points using the same model.
In the VARIABLE command, the NAMES option is used to assign names to the variables in the data set. The data set in this example contains one variable y. The variable y is measured over multiple time points. The number of times it is measured is equal to the number of records in the data set. The records must be ordered by time. The LAGGED option is used to specify the maximum lag to use for an observed variable during model estimation. The variable y has lag 1. The lagged variable is referred to by adding to the name of the variable an ampersand (&) and the number of the lag.
In the ANALYSIS command, by specifying ESTIMATOR=BAYES, a Bayesian analysis will be carried out. In Bayesian estimation, the default is to use two independent Markov chain Monte Carlo (MCMC) chains. If multiple processors are available, using PROCESSORS=2 will speed up computations. The BITERATIONS option is used to specify the maximum and minimum number of iterations for each Markov chain Monte Carlo (MCMC) chain when the potential scale reduction (PSR) convergence criterion (Gelman & Rubin, 1992) is used. Using a number in parentheses, the BITERATIONS option specifies that a minimum of 2,000 and a maximum of the default of 50,000 iterations will be used.
In the MODEL command, the ON statement describes the linear regression over multiple time points of the dependent variable y on the dependent variable y&1 which is y at the previous time point. An intercept, regression coefficient, and residual variance are estimated.
An N=1 time series analysis with a univariate second-order autoregressive AR(2) model can also be estimated. For this analysis, the LAGGED option is specified as LAGGED = y (2); and the MODEL command is specified as follows:
MODEL: y ON y&1 y&2;
In the MODEL command, the ON statement describes the linear regression over multiple time points of the dependent variable y on the dependent variable y&1 which is y at the previous time point and the dependent variable y&2 which is y at two time points prior. An intercept, two regression coefficients, and a residual variance are estimated. A model where only y at lag 2 is used is specified as follows:
MODEL: y ON y&1@0 y&2;
where the coefficient for y at lag 1 is fixed at zero. An intercept, regression coefficient, and residual variance are estimated.
The OUTPUT command is used to request additional output not included as the default. The TECH1 option is used to request the arrays containing parameter specifications and starting values for all free parameters in the model. The TECH8 option is used to request that the optimization history in estimating the model be printed in the output. TECH8 is printed to the screen during the computations as the default. TECH8 screen printing is useful for determining how long the analysis takes and to check convergence using the PSR convergence criterion. The PLOT command is used to request graphical displays of observed data and analysis results. These graphical displays can be viewed after the analysis is completed using a post-processing graphics module. The trace plot and autocorrelation plot can be used to monitor the MCMC iterations in terms of convergence and quality of the posterior distribution for each parameter. The posterior distribution plot shows the complete posterior distribution of the parameter estimate. Also available are time series plots of observed values, autocorrelations at different lags, and partial autocorrelations at different lags. An explanation of the other commands can be found in Example 6.1.
TITLE: this is an example of an N=1 time series analysis with a univariate first-order autoregressive AR(1) model for a continuous dependent variable with a covariate
DATA: FILE = ex6.24.dat;
VARIABLE: NAMES ARE y x;
LAGGED = y(1) x(1);
ANALYSIS: ESTIMATOR = BAYES;
PROCESSORS = 2;
BITERATIONS = (1000);
MODEL: y ON y&1 x x&1;
OUTPUT: TECH1 TECH8;
PLOT: TYPE = PLOT3;
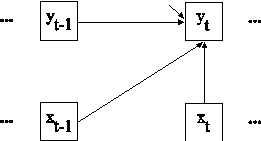
In this example, the N=1 time series analysis with a univariate first-order autoregressive AR(1) model for a continuous dependent variable with a covariate shown in the picture above is estimated. The subscript t refers to a time point and the subscript t-1 refers to the previous time point. The dots indicate that the process includes both previous and future time points using the same model.
In the MODEL command, the ON statement describes the linear regression over multiple time points of the dependent variable y on the dependent variable y&1 which is y at the previous time point, a covariate x, and a covariate x&1 which is x at the previous time point. An intercept, three regression coefficients, and a residual variance are estimated. An explanation of the other commands can be found in Examples 6.1 and 6.23.
TITLE: this is an example of an N=1 time series analysis with a bivariate cross-lagged model for continuous dependent variables
DATA: FILE = ex6.25.dat;
VARIABLE: NAMES = y1 y2;
LAGGED = y1(1) y2(1);
ANALYSIS: ESTIMATOR = BAYES;
PROCESSORS = 2;
BITERATIONS = (500);
MODEL: y1 ON y1&1 y2&1;
y2 ON y2&1 y1&1;
OUTPUT: TECH1 TECH8;
PLOT: TYPE = PLOT3;
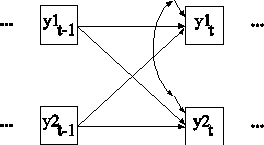
In this example, the N=1 time series analysis with a bivariate cross-lagged model for continuous dependent variables shown in the picture above is estimated. This model is also referred to as a first-order vector autoregressive VAR(1) model, see e.g., Shumway and Stoffer (2011). The subscript t refers to a time point and the subscript t-1 refers to the previous time point. The dots indicate that the process includes both previous and future time points using the same model.
In the MODEL command, the first ON statement describes the linear regression over multiple time points of the dependent variable y1 on the dependent variable y1&1 which is y1 at the previous time point, and the dependent variable y2&1 which is y2 at the previous time point. The second ON statement describes the linear regression over multiple time points of the dependent variable y2 on the dependent variable y2&1 which is y2 at the previous time point, and the dependent variable y1&1 which is y1 at the previous time point. Two intercepts, four regression coefficients, two residual variances, and one residual covariance are estimated. An explanation of the other commands can be found in Examples 6.1 and 6.23.
TITLE: this is an example of an N=1 time series analysis with a first-order autoregressive AR(1) confirmatory factor analysis (CFA) model with continuous factor indicators
DATA: FILE = ex6.26.dat;
VARIABLE: NAMES = y1-y4;
ANALYSIS: ESTIMATOR = BAYES;
PROCESSORS = 2;
BITERATIONS = (2000);
MODEL: f BY y1-y4 (&1);
f ON f&1;
OUTPUT: TECH1 TECH8;
PLOT: TYPE = PLOT3;

In this example, the N=1 time series analysis with a first-order autoregressive AR(1) confirmatory factor analysis (CFA) model with continuous factor indicators shown in the picture above is estimated. This model is also referred to as a direct autoregressive factor score (DAFS) model. For a discussion of N=1 time series factor analysis, also referred to as dynamic factor analysis, see e.g., Molenaar (1985); Zhang, Hamaker, and Nesselroade (2008); and Asparouhov, Hamaker, and Muthén (2017). The subscript t refers to a time point and the subscript t-1 refers to the previous time point. The dots indicate that the process includes both previous and future time points using the same model.
In the MODEL command, the BY statement specifies that f is measured by y1, y2, y3, and y4. The metric of the factor is set automatically by the program by fixing the first factor loading to one. This option can be overridden. An ampersand (&) followed by the number 1 is placed in parentheses following the BY statement to indicate that the factor f at lag 1 can be used in the analysis. The factor f at lag 1 is referred to as f&1. The intercepts and residual variances of the factor indicators are estimated and the residuals are not correlated as the default. The ON statement describes the linear regression over multiple time points of the factor f on the factor f&1 which is f at the previous time point. A regression coefficient and residual variance of the factor are estimated. The intercept of the factor is fixed at zero as the default.
A white noise factor score (WNFS) model (Zhang & Nesselroade, 2007) can be estimated using the MODEL command below where instead of regressing the factor f on f&1, the factor indicators y1, y2, y3, and y4 are regressed on f&1.
MODEL: f BY y1-y4 (&1);
y1-y4 ON f&1;
An explanation of the other commands can be found in Examples 6.1 and 6.23.
TITLE: this is an example of an N=1 time series analysis with a first-order autoregressive AR(1) IRT model with binary factor indicators
DATA: FILE = ex6.27.dat;
VARIABLE: NAMES = u1-u4;
CATEGORICAL = u1-u4;
ANALYSIS: ESTIMATOR = BAYES;
PROCESSORS = 2;
BITERATIONS = (2000);
MODEL: f BY u1-u4*(&1);
f@1;
f ON f&1;
OUTPUT: TECH1 TECH8;
PLOT: TYPE = PLOT3;
In this example, an N=1 time series analysis with a first-order autoregressive AR(1) IRT model with binary factor indicators is estimated. The subscript t refers to a time point and the subscript t-1 refers to the previous time point. The dots indicate that the process includes both previous and future time points using the same model.
The CATEGORICAL option specifies that the variables u1, u2, u3, and u4 are binary. In the MODEL command, the BY statement specifies that f is measured by u1, u2, u3, and u4. The metric of the factor is set automatically by the program by fixing the first factor loading to one. The asterisk following u1-u4 overrides this default. The metric of the factor is set by fixing the factor residual variance to one. An ampersand (&) followed by the number 1 is placed in parentheses following the BY statement to indicate that the factor f at lag 1 can be used in the analysis. The factor f at lag 1 is referred to as f&1. The thresholds of the factor indicators are estimated as the default. The ON statement describes the linear regression over multiple time points of the factor f on the factor f&1 which is f at the previous time point. A regression coefficient and residual variance of the factor are estimated. The intercept of the factor is fixed at zero as the default. An explanation of the other commands can be found in Examples 6.1, 6.4, and 6.23.
TITLE: this is an example of an N=1 time series analysis with a bivariate cross-lagged model with two factors and continuous factor indicators
DATA: FILE = ex6.28.dat;
VARIABLE: NAMES = y11-y14 y21-y24;
ANALYSIS: ESTIMATOR = BAYES;
PROCESSORS = 2;
BITERATIONS = (2000);
MODEL: f1 BY y11-y14 (&1);
f2 BY y21-y24 (&1);
f1 ON f1&1 f2&1;
f2 ON f2&1 f1&1;
OUTPUT: TECH1 TECH8;
PLOT: TYPE = PLOT3;
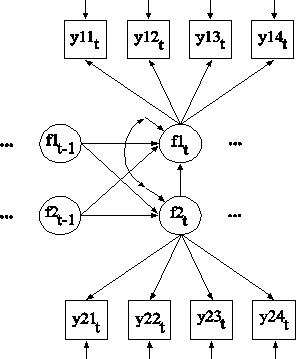
In this example, the N=1 time series analysis with a bivariate cross-lagged model with two factors and continuous factor indicators shown in the picture above is estimated. The subscript t refers to a time point and the subscript t-1 refers to the previous time point. The dots indicate that the process includes both previous and future time points using the same model.
In the MODEL command, the first BY statement specifies that f1 is measured by y11, y12, y13, and y14. The second BY statement specifies that f2 is measured by y21, y22, y23, and y24. The metric of the factors is set automatically by the program by fixing the first factor loading to one. This option can be overridden. An ampersand (&) followed by the number 1 is placed in parentheses following the BY statements to indicate that the factors f1 and f2 at lag 1 are used during model estimation. The factors f1 and f2 at lag 1 are referred to as f1&1 and f2&1, respectively. The intercepts and residual variances of the factor indicators are estimated and the residuals are not correlated as the default. The first ON statement describes the linear regression over multiple time points of the factor f1 on the factor f1&1 which is f1 at the previous time point and the factor f2&1 which is f2 at the previous time point. The second ON statement describes the linear regression over multiple time points of the factor f2 on the factor f2&1 which is f2 at the previous time point and the factor f1&1 which is f1 at the previous time point. Four regression coefficients, two residual variances, and one residual covariance of the factors are estimated. The intercepts of the factors are fixed at zero as the default. An explanation of the other commands can be found in Examples 6.1 and 6.23.