CHAPTER 8
EXAMPLES: MIXTURE MODELING WITH LONGITUDINAL DATA
Mixture modeling refers to modeling with categorical latent variables that represent subpopulations where population membership is not known but is inferred from the data. This is referred to as finite mixture modeling in statistics (McLachlan & Peel, 2000). For an overview of different mixture models, see Muthén (2008). In mixture modeling with longitudinal data, unobserved heterogeneity in the development of an outcome over time is captured by categorical and continuous latent variables. The simplest longitudinal mixture model is latent class growth analysis (LCGA). In LCGA, the mixture corresponds to different latent trajectory classes. No variation across individuals is allowed within classes (Nagin, 1999; Roeder, Lynch, & Nagin, 1999; Kreuter & Muthén, 2008). Another longitudinal mixture model is the growth mixture model (GMM; Muthén & Shedden, 1999; Muthén et al., 2002; Muthén, 2004; Muthén & Asparouhov, 2009). In GMM, within-class variation of individuals is allowed for the latent trajectory classes. The within-class variation is represented by random effects, that is, continuous latent variables, as in regular growth modeling. All of the growth models discussed in Chapter 6 can be generalized to mixture modeling. Yet another mixture model for analyzing longitudinal data is latent transition analysis (LTA; Collins & Wugalter, 1992; Reboussin et al., 1998), also referred to as hidden Markov modeling, where latent class indicators are measured over time and individuals are allowed to transition between latent classes. With discrete-time survival mixture analysis (DTSMA; Muthén & Masyn, 2005), the repeated observed outcomes represent event histories. Continuous-time survival mixture modeling is also available (Asparouhov et al., 2006). For mixture modeling with longitudinal data, observed outcome variables can be continuous, censored, binary, ordered categorical (ordinal), counts, or combinations of these variable types.
All longitudinal mixture models can be estimated using the following special features:
· Single or multiple group analysis
· Missing data
· Complex survey data
· Latent variable interactions and non-linear factor analysis using maximum likelihood
· Random slopes
· Individually-varying times of observations
· Linear and non-linear parameter constraints
· Indirect effects including specific paths
· Maximum likelihood estimation for all outcome types
· Bootstrap standard errors and confidence intervals
· Wald chi-square test of parameter equalities
· Test of equality of means across latent classes using posterior probability-based multiple imputations
For TYPE=MIXTURE, multiple group analysis is specified by using the KNOWNCLASS option of the VARIABLE command. The default is to estimate the model under missing data theory using all available data. The LISTWISE option of the DATA command can be used to delete all observations from the analysis that have missing values on one or more of the analysis variables. Corrections to the standard errors and chi-square test of model fit that take into account stratification, non-independence of observations, and unequal probability of selection are obtained by using the TYPE=COMPLEX option of the ANALYSIS command in conjunction with the STRATIFICATION, CLUSTER, and WEIGHT options of the VARIABLE command. The SUBPOPULATION option is used to select observations for an analysis when a subpopulation (domain) is analyzed. Latent variable interactions are specified by using the | symbol of the MODEL command in conjunction with the XWITH option of the MODEL command. Random slopes are specified by using the | symbol of the MODEL command in conjunction with the ON option of the MODEL command. Individually-varying times of observations are specified by using the | symbol of the MODEL command in conjunction with the AT option of the MODEL command and the TSCORES option of the VARIABLE command. Linear and non-linear parameter constraints are specified by using the MODEL CONSTRAINT command. Indirect effects are specified by using the MODEL INDIRECT command. Maximum likelihood estimation is specified by using the ESTIMATOR option of the ANALYSIS command. Bootstrap standard errors are obtained by using the BOOTSTRAP option of the ANALYSIS command. Bootstrap confidence intervals are obtained by using the BOOTSTRAP option of the ANALYSIS command in conjunction with the CINTERVAL option of the OUTPUT command. The MODEL TEST command is used to test linear restrictions on the parameters in the MODEL and MODEL CONSTRAINT commands using the Wald chi-square test. The AUXILIARY option is used to test the equality of means across latent classes using posterior probability-based multiple imputations.
Graphical displays of observed data and analysis results can be obtained using the PLOT command in conjunction with a post-processing graphics module. The PLOT command provides histograms, scatterplots, plots of individual observed and estimated values, plots of sample and estimated means and proportions/probabilities, and plots of estimated probabilities for a categorical latent variable as a function of its covariates. These are available for the total sample, by group, by class, and adjusted for covariates. The PLOT command includes a display showing a set of descriptive statistics for each variable. The graphical displays can be edited and exported as a DIB, EMF, or JPEG file. In addition, the data for each graphical display can be saved in an external file for use by another graphics program.
Following is the set of GMM examples included in this chapter:
· 8.1: GMM for a continuous outcome using automatic starting values and random starts
· 8.2: GMM for a continuous outcome using user-specified starting values and random starts
· 8.3: GMM for a censored outcome using a censored model with automatic starting values and random starts*
· 8.4: GMM for a categorical outcome using automatic starting values and random starts*
· 8.5: GMM for a count outcome using a zero-inflated Poisson model and a negative binomial model with automatic starting values and random starts*
· 8.6: GMM with a categorical distal outcome using automatic starting values and random starts
· 8.7: A sequential process GMM for continuous outcomes with two categorical latent variables
· 8.8: GMM with known classes (multiple group analysis)
Following is the set of LCGA examples included in this chapter:
· 8.9: LCGA for a binary outcome
· 8.10: LCGA for a three-category outcome
· 8.11: LCGA for a count outcome using a zero-inflated Poisson model
Following is the set of hidden Markov and LTA examples included in this chapter:
· 8.12: Hidden Markov model with four time points
· 8.13: LTA for two time points with a binary covariate influencing the latent transition probabilities
· 8.14: LTA for two time points with a continuous covariate influencing the latent transition probabilities
· 8.15: Mover-stayer LTA for three time points using a probability parameterization
Following are the discrete-time and continuous-time survival mixture analysis examples included in this chapter:
· 8.16: Discrete-time survival mixture analysis with survival predicted by growth trajectory classes
· 8.17: Continuous-time survival mixture analysis using a Cox regression model
* Example uses numerical integration in the estimation of the model. This can be computationally demanding depending on the size of the problem.
TITLE: this is an example of a GMM for a continuous outcome using automatic starting values and random starts
DATA: FILE IS ex8.1.dat;
VARIABLE: NAMES ARE y1–y4 x;
CLASSES = c (2);
ANALYSIS: TYPE = MIXTURE;
STARTS = 40 8;
MODEL:
%OVERALL%
i s | y1@0 y2@1 y3@2 y4@3;
i s ON x;
c ON x;
OUTPUT: TECH1 TECH8;
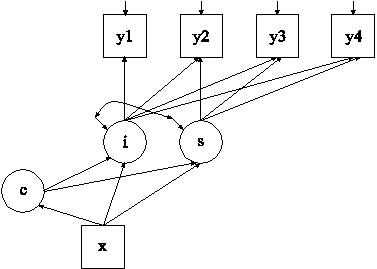
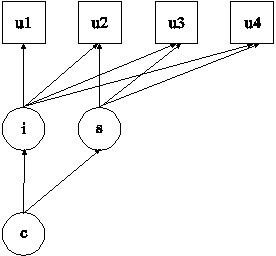
In the example above, the growth mixture model (GMM) for a continuous outcome shown in the picture above is estimated. Because c is a categorical latent variable, the interpretation of the picture is not the same as for models with continuous latent variables. The arrows from c to the growth factors i and s indicate that the intercepts in the regressions of the growth factors on x vary across the classes of c. This corresponds to the regressions of i and s on a set of dummy variables representing the categories of c. The arrow from x to c represents the multinomial logistic regression of c on x. GMM is discussed in Muthén and Shedden (1999), Muthén (2004), and Muthén and Asparouhov (2009).
TITLE: this is an example of a growth mixture model for a continuous outcome
The TITLE command is used to provide a title for the analysis. The title is printed in the output just before the Summary of Analysis.
DATA: FILE IS ex8.1.dat;
The DATA command is used to provide information about the data set to be analyzed. The FILE option is used to specify the name of the file that contains the data to be analyzed, ex8.1.dat. Because the data set is in free format, the default, a FORMAT statement is not required.
VARIABLE: NAMES ARE y1–y4 x;
CLASSES = c (2);
The VARIABLE command is used to provide information about the variables in the data set to be analyzed. The NAMES option is used to assign names to the variables in the data set. The data set in this example contains five variables: y1, y2, y3, y4, and x. Note that the hyphen can be used as a convenience feature in order to generate a list of names. The CLASSES option is used to assign names to the categorical latent variables in the model and to specify the number of latent classes in the model for each categorical latent variable. In the example above, there is one categorical latent variable c that has two latent classes.
ANALYSIS: TYPE = MIXTURE;
STARTS = 40 8;
The ANALYSIS command is used to describe the technical details of the analysis. The TYPE option is used to describe the type of analysis that is to be performed. By selecting MIXTURE, a mixture model will be estimated.
When TYPE=MIXTURE is specified, either user-specified or automatic starting values are used to create randomly perturbed sets of starting values for all parameters in the model except variances and covariances. In this example, the random perturbations are based on automatic starting values. Maximum likelihood optimization is done in two stages. In the initial stage, 20 random sets of starting values are generated. An optimization is carried out for 10 iterations using each of the 20 random sets of starting values. The ending values from the 4 optimizations with the highest loglikelihoods are used as the starting values in the final stage optimizations which is carried out using the default optimization settings for TYPE=MIXTURE. A more thorough investigation of multiple solutions can be carried out using the STARTS and STITERATIONS options of the ANALYSIS command. In this example, 40 initial stage random sets of starting values are used and 8 final stage optimizations are carried out.
MODEL:
%OVERALL%
i s | y1@0 y2@1 y3@2 y4@3;
i s ON x;
c ON x;
The MODEL command is used to describe the model to be estimated. For mixture models, there is an overall model designated by the label %OVERALL%. The overall model describes the part of the model that is in common for all latent classes. The | symbol is used to name and define the intercept and slope growth factors in a growth model. The names i and s on the left-hand side of the | symbol are the names of the intercept and slope growth factors, respectively. The statement on the right-hand side of the | symbol specifies the outcome and the time scores for the growth model. The time scores for the slope growth factor are fixed at 0, 1, 2, and 3 to define a linear growth model with equidistant time points. The zero time score for the slope growth factor at time point one defines the intercept growth factor as an initial status factor. The coefficients of the intercept growth factor are fixed at one as part of the growth model parameterization. The residual variances of the outcome variables are estimated and allowed to be different across time and the residuals are not correlated as the default.
In the parameterization of the growth model shown here, the intercepts of the outcome variable at the four time points are fixed at zero as the default. The intercepts and residual variances of the growth factors are estimated as the default, and the growth factor residual covariance is estimated as the default because the growth factors do not influence any variable in the model except their own indicators. The intercepts of the growth factors are not held equal across classes as the default. The residual variances and residual covariance of the growth factors are held equal across classes as the default.
The first ON statement describes the linear regressions of the intercept and slope growth factors on the covariate x. The second ON statement describes the multinomial logistic regression of the categorical latent variable c on the covariate x when comparing class 1 to class 2. The intercept of this regression is estimated as the default. The default estimator for this type of analysis is maximum likelihood with robust standard errors. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator.
Following is an alternative specification of the multinomial logistic regression of c on the covariate x:
c#1 ON x;
where c#1 refers to the first class of c. The classes of a categorical latent variable are referred to by adding to the name of the categorical latent variable the number sign (#) followed by the number of the class. This alternative specification allows individual parameters to be referred to in the MODEL command for the purpose of giving starting values or placing restrictions.
OUTPUT: TECH1 TECH8;
The OUTPUT command is used to request additional output not included as the default. The TECH1 option is used to request the arrays containing parameter specifications and starting values for all free parameters in the model. The TECH8 option is used to request that the optimization history in estimating the model be printed in the output. TECH8 is printed to the screen during the computations as the default. TECH8 screen printing is useful for determining how long the analysis takes.
TITLE: this is an example of a GMM for a continuous outcome using user-specified starting values and random starts
DATA: FILE IS ex8.2.dat;
VARIABLE: NAMES ARE y1–y4 x;
CLASSES = c (2);
ANALYSIS: TYPE = MIXTURE;
MODEL:
%OVERALL%
i s | y1@0 y2@1 y3@2 y4@3;
i s ON x;
c ON x;
%c#1%
[i*1 s*.5];
%c#2%
[i*3 s*1];
OUTPUT: TECH1 TECH8;
The difference between this example and Example 8.1 is that user-specified starting values are used instead of automatic starting values. In the MODEL command, user-specified starting values are given for the intercepts of the intercept and slope growth factors. Intercepts are referred to using brackets statements. The asterisk (*) is used to assign a starting value for a parameter. It is placed after the parameter with the starting value following it. In class 1, a starting value of 1 is given for the intercept growth factor and a starting value of .5 is given for the slope growth factor. In class 2, a starting value of 3 is given for the intercept growth factor and a starting value of 1 is given for the slope growth factor. The default estimator for this type of analysis is maximum likelihood with robust standard errors. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. An explanation of the other commands can be found in Example 8.1.
TITLE: this is an example of a GMM for a censored outcome using a censored model with automatic starting values and random starts
DATA: FILE IS ex8.3.dat;
VARIABLE: NAMES ARE y1-y4 x;
CLASSES = c (2);
CENSORED = y1-y4 (b);
ANALYSIS: TYPE = MIXTURE;
ALGORITHM = INTEGRATION;
MODEL:
%OVERALL%
i s | y1@0 y2@1 y3@2 y4@3;
i s ON x;
c ON x;
OUTPUT: TECH1 TECH8;
The difference between this example and Example 8.1 is that the outcome variable is a censored variable instead of a continuous variable. The CENSORED option is used to specify which dependent variables are treated as censored variables in the model and its estimation, whether they are censored from above or below, and whether a censored or censored-inflated model will be estimated. In the example above, y1, y2, y3, and y4 are censored variables. They represent the outcome variable measured at four equidistant occasions. The b in parentheses following y1-y4 indicates that y1, y2, y3, and y4 are censored from below, that is, have floor effects, and that the model is a censored regression model. The censoring limit is determined from the data.
By specifying ALGORITHM=INTEGRATION, a maximum likelihood estimator with robust standard errors using a numerical integration algorithm will be used. Note that numerical integration becomes increasingly more computationally demanding as the number of factors and the sample size increase. In this example, two dimensions of integration are used with a total of 225 integration points. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator.
In the parameterization of the growth model shown here, the intercepts of the outcome variable at the four time points are fixed at zero as the default. The intercepts and residual variances of the growth factors are estimated as the default, and the growth factor residual covariance is estimated as the default because the growth factors do not influence any variable in the model except their own indicators. The intercepts of the growth factors are not held equal across classes as the default. The residual variances and residual covariance of the growth factors are held equal across classes as the default. An explanation of the other commands can be found in Example 8.1.
TITLE: this is an example of a GMM for a categorical outcome using automatic starting values and random starts
DATA: FILE IS ex8.4.dat;
VARIABLE: NAMES ARE u1–u4 x;
CLASSES = c (2);
CATEGORICAL = u1-u4;
ANALYSIS: TYPE = MIXTURE;
ALGORITHM = INTEGRATION;
MODEL:
%OVERALL%
i s | u1@0 u2@1 u3@2 u4@3;
i s ON x;
c ON x;
OUTPUT: TECH1 TECH8;
The difference between this example and Example 8.1 is that the outcome variable is a binary or ordered categorical (ordinal) variable instead of a continuous variable. The CATEGORICAL option is used to specify which dependent variables are treated as binary or ordered categorical (ordinal) variables in the model and its estimation. In the example above, u1, u2, u3, and u4 are binary or ordered categorical variables. They represent the outcome variable measured at four equidistant occasions.
By specifying ALGORITHM=INTEGRATION, a maximum likelihood estimator with robust standard errors using a numerical integration algorithm will be used. Note that numerical integration becomes increasingly more computationally demanding as the number of factors and the sample size increase. In this example, two dimensions of integration are used with a total of 225 integration points. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator.
In the parameterization of the growth model shown here, the thresholds of the outcome variable at the four time points are held equal as the default. The intercept of the intercept growth factor is fixed at zero in the last class and is free to be estimated in the other classes. The intercept of the slope growth factor and the residual variances of the intercept and slope growth factors are estimated as the default, and the growth factor residual covariance is estimated as the default because the growth factors do not influence any variable in the model except their own indicators. The intercepts of the growth factors are not held equal across classes as the default. The residual variances and residual covariance of the growth factors are held equal across classes as the default. An explanation of the other commands can be found in Example 8.1.
TITLE: this is an example of a GMM for a count outcome using a zero-inflated Poisson model with automatic starting values and random starts
DATA: FILE IS ex8.5a.dat;
VARIABLE: NAMES ARE u1–u8 x;
CLASSES = c (2);
COUNT ARE u1-u8 (i);
ANALYSIS: TYPE = MIXTURE;
STARTS = 40 8;
STITERATIONS = 20;
ALGORITHM = INTEGRATION;
MODEL:
%OVERALL%
i s q | u1@0 u2@.1 u3@.2 u4@.3 u5@.4 u6@.5
u7@.6 u8@.7;
ii si qi | u1#1@0 u2#1@.1 u3#1@.2 u4#1@.3 u5#1@.4 u6#1@.5 u7#1@.6 u8#1@.7;
s-qi@0;
i s ON x;
c ON x;
OUTPUT: TECH1 TECH8;
The difference between this example and Example 8.1 is that the outcome variable is a count variable instead of a continuous variable. In addition, the outcome is measured at eight occasions instead of four and a quadratic rather than a linear growth model is estimated. The COUNT option is used to specify which dependent variables are treated as count variables in the model and its estimation and the type of model that will be estimated. In the first part of this example a zero-inflated Poisson model is estimated. In the example above, u1, u2, u3, u4, u5, u6, u7, and u8 are count variables. They represent the outcome variable measured at eight equidistant occasions. The i in parentheses following u1-u8 indicates that a zero-inflated Poisson model will be estimated.
A more thorough investigation of multiple solutions can be carried out using the STARTS and STITERATIONS options of the ANALYSIS command. In this example, 40 initial stage random sets of starting values are used and 8 final stage optimizations are carried out. In the initial stage analyses, 20 iterations are used instead of the default of 10 iterations. By specifying ALGORITHM=INTEGRATION, a maximum likelihood estimator with robust standard errors using a numerical integration algorithm will be used. Note that numerical integration becomes increasingly more computationally demanding as the number of factors and the sample size increase. In this example, one dimension of integration is used with 15 integration points. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator.
With a zero-inflated Poisson model, two growth models are estimated. The first | statement describes the growth model for the count part of the outcome for individuals who are able to assume values of zero and above. The second | statement describes the growth model for the inflation part of the outcome, the probability of being unable to assume any value except zero. The binary latent inflation variable is referred to by adding to the name of the count variable the number sign (#) followed by the number 1.
In the parameterization of the growth model for the count part of the outcome, the intercepts of the outcome variable at the eight time points are fixed at zero as the default. The intercepts and residual variances of the growth factors are estimated as the default, and the growth factor residual covariances are estimated as the default because the growth factors do not influence any variable in the model except their own indicators. The intercepts of the growth factors are not held equal across classes as the default. The residual variances and residual covariances of the growth factors are held equal across classes as the default. In this example, the variances of the slope growth factors s and q are fixed at zero. This implies that the covariances between i, s, and q are fixed at zero. Only the variance of the intercept growth factor i is estimated.
In the parameterization of the growth model for the inflation part of the outcome, the intercepts of the outcome variable at the eight time points are held equal as the default. The intercept of the intercept growth factor is fixed at zero in all classes as the default. The intercept of the slope growth factor and the residual variances of the intercept and slope growth factors are estimated as the default, and the growth factor residual covariances are estimated as the default because the growth factors do not influence any variable in the model except their own indicators. The intercept of the slope growth factor, the residual variances of the growth factors, and residual covariance of the growth factors are held equal across classes as the default. These defaults can be overridden, but freeing too many parameters in the inflation part of the model can lead to convergence problems. In this example, the variances of the intercept and slope growth factors are fixed at zero. This implies that the covariances between ii, si, and qi are fixed at zero. An explanation of the other commands can be found in Example 8.1.
TITLE: this is an example of a GMM for a count
outcome using a negative binomial model with automatic starting values and random starts
DATA: FILE IS ex8.5b.dat;
VARIABLE: NAMES ARE u1-u8 x;
CLASSES = c(2);
COUNT = u1-u8(nb);
ANALYSIS: TYPE = MIXTURE;
ALGORITHM = INTEGRATION;
MODEL:
%OVERALL%
i s q | u1@0 u2@.1 u3@.2 u4@.3 u5@.4 u6@.5 u7@.6 u8@.7;
s-q@0;
i s ON x;
c ON x;
OUTPUT: TECH1 TECH8;
The difference between this part of the example and the first part is that a growth mixture model (GMM) for a count outcome using a negative binomial model is estimated instead of a zero-inflated Poisson model. The negative binomial model estimates a dispersion parameter for each of the outcomes (Long, 1997; Hilbe, 2011).
The COUNT option is used to specify which dependent variables are treated as count variables in the model and its estimation and which type of model is estimated. The nb in parentheses following u1-u8 indicates that a negative binomial model will be estimated. The dispersion parameters for each of the outcomes are held equal across classes as the default. The dispersion parameters can be referred to using the names of the count variables. An explanation of the other commands can be found in the first part of this example and in Example 8.1.
EXAMPLE 8.6: GMM WITH A CATEGORICAL DISTAL OUTCOME USING AUTOMATIC STARTING VALUES AND RANDOM STARTS
TITLE: this is an example of a GMM with a categorical distal outcome using automatic starting values and random starts
DATA: FILE IS ex8.6.dat;
VARIABLE: NAMES ARE y1–y4 u x;
CLASSES = c(2);
CATEGORICAL = u;
ANALYSIS: TYPE = MIXTURE;
MODEL:
%OVERALL%
i s | y1@0 y2@1 y3@2 y4@3;
i s ON x;
c ON x;
OUTPUT: TECH1 TECH8;
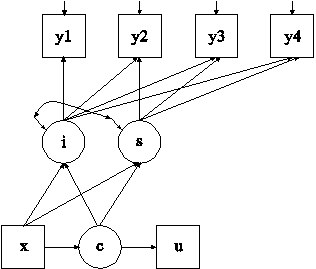
The difference between this example and Example 8.1 is that a binary or ordered categorical (ordinal) distal outcome has been added to the model as shown in the picture above. The distal outcome u is regressed on the categorical latent variable c using logistic regression. This is represented as the thresholds of u varying across classes.
The CATEGORICAL option is used to specify which dependent variables are treated as binary or ordered categorical (ordinal) variables in the model and its estimation. In the example above, u is a binary or ordered categorical variable. The program determines the number of categories for each indicator. The default is that the thresholds of u are estimated and vary across the latent classes. Because automatic starting values are used, it is not necessary to include these class-specific statements in the model command. The default estimator for this type of analysis is maximum likelihood with robust standard errors. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. An explanation of the other commands can be found in Example 8.1.
TITLE: this is an example of a sequential
process GMM for continuous outcomes with
two categorical latent variables
DATA: FILE IS ex8.7.dat;
VARIABLE: NAMES ARE y1-y8;
CLASSES = c1 (3) c2 (2);
ANALYSIS: TYPE = MIXTURE;
MODEL:
%OVERALL%
i1 s1 | y1@0 y2@1 y3@2 y4@3;
i2 s2 | y5@0 y6@1 y7@2 y8@3;
c2 ON c1;
MODEL c1:
%c1#1%
[i1 s1];
%c1#2%
[i1*1 s1];
%c1#3%
[i1*2 s1];
MODEL c2:
%c2#1%
[i2 s2];
%c2#2%
[i2*-1 s2];
OUTPUT: TECH1 TECH8;
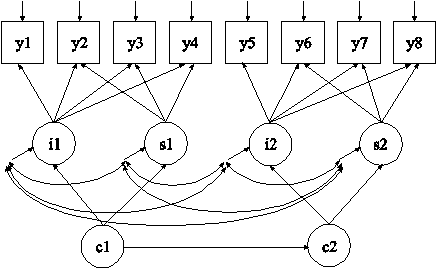
In this example, the sequential process growth mixture model for continuous outcomes shown in the picture above is estimated. The latent classes of the second process are related to the latent classes of the first process. This is a type of latent transition analysis. Latent transition analysis is shown in Examples 8.12, 8.13, and 8.14.
The | statements in the overall model are used to name and define the intercept and slope growth factors in the growth models. In the first | statement, the names i1 and s1 on the left-hand side of the | symbol are the names of the intercept and slope growth factors, respectively. In the second | statement, the names i2 and s2 on the left-hand side of the | symbol are the names of the intercept and slope growth factors, respectively. In both | statements, the values on the right-hand side of the | symbol are the time scores for the slope growth factor. For both growth processes, the time scores of the slope growth factors are fixed at 0, 1, 2, and 3 to define linear growth models with equidistant time points. The zero time scores for the slope growth factors at time point one define the intercept growth factors as initial status factors. The coefficients of the intercept growth factors i1 and i2 are fixed at one as part of the growth model parameterization. In the parameterization of the growth model shown here, the means of the outcome variables at the four time points are fixed at zero as the default. The intercept and slope growth factor means are estimated as the default. The variances of the growth factors are also estimated as the default. The growth factors are correlated as the default because they are independent (exogenous) variables. The means of the growth factors are not held equal across classes as the default. The variances and covariances of the growth factors are held equal across classes as the default.
In the overall model, the ON statement describes the probabilities of transitioning from a class of the categorical latent variable c1 to a class of the categorical latent variable c2. The ON statement describes the multinomial logistic regression of c2 on c1 when comparing class 1 of c2 to class 2 of c2. In this multinomial logistic regression, coefficients corresponding to the last class of each of the categorical latent variables are fixed at zero. The parameterization of models with more than one categorical latent variable is discussed in Chapter 14. Because c1 has three classes and c2 has two classes, two regression coefficients are estimated. The means of c1 and the intercepts of c2 are estimated as the default.
When there are multiple categorical latent variables, each one has its own MODEL command. The MODEL command for each latent variable is specified by MODEL followed by the name of the latent variable. For each categorical latent variable, the part of the model that differs for each class is specified by a label that consists of the categorical latent variable followed by the number sign followed by the class number. In the example above, the label %c1#1% refers to the part of the model for class one of the categorical latent variable c1 that differs from the overall model. The label %c2#1% refers to the part of the model for class one of the categorical latent variable c2 that differs from the overall model. The class-specific part of the model for each categorical latent variable specifies that the means of the intercept and slope growth factors are free to be estimated for each class. The default estimator for this type of analysis is maximum likelihood with robust standard errors. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. An explanation of the other commands can be found in Example 8.1.
Following is an alternative specification of the multinomial logistic regression of c2 on c1:
c2#1 ON c1#1 c1#2;
where c2#1 refers to the first class of c2, c1#1 refers to the first class of c1, and c1#2 refers to the second class of c1. The classes of a categorical latent variable are referred to by adding to the name of the categorical latent variable the number sign (#) followed by the number of the class. This alternative specification allows individual parameters to be referred to in the MODEL command for the purpose of giving starting values or placing restrictions.
TITLE: this is an example of GMM with known classes (multiple group analysis)
DATA: FILE IS ex8.8.dat;
VARIABLE: NAMES ARE g y1-y4 x;
USEVARIABLES ARE y1-y4 x;
CLASSES = cg (2) c (2);
KNOWNCLASS = cg (g = 0 g = 1);
ANALYSIS: TYPE = MIXTURE;
MODEL:
%OVERALL%
i s | y1@0 y2@1 y3@2 y4@3;
i s ON x;
c ON cg x;
%cg#1.c#1%
[i*2 s*1];
%cg#1.c#2%
[i*0 s*0];
%cg#2.c#1%
[i*3 s*1.5];
%cg#2.c#2%
[i*1 s*.5];
OUTPUT: TECH1 TECH8;
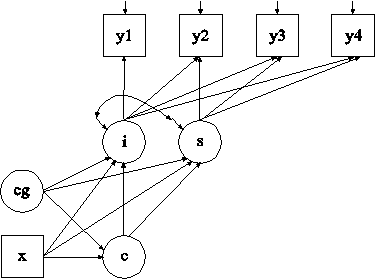
The difference between this example and Example 8.1 is that this analysis includes a categorical latent variable for which class membership is known resulting in a multiple group growth mixture model. The CLASSES option is used to assign names to the categorical latent variables in the model and to specify the number of latent classes in the model for each categorical latent variable. In the example above, there are two categorical latent variables cg and c. Both categorical latent variables have two latent classes. The KNOWNCLASS option is used for multiple group analysis with TYPE=MIXTURE to identify the categorical latent variable for which latent class membership is known and is equal to observed groups in the sample. The KNOWNCLASS option identifies cg as the categorical latent variable for which class membership is known. The information in parentheses following the categorical latent variable name defines the known classes using an observed variable. In this example, the observed variable g is used to define the known classes. The first class consists of individuals with the value 0 on the variable g. The second class consists of individuals with the value 1 on the variable g.
In the overall model, the second ON statement describes the multinomial logistic regression of the categorical latent variable c on the known class variable cg and the covariate x. This allows the class probabilities to vary across the observed groups in the sample. In the four class-specific parts of the model, starting values are given for the growth factor intercepts. The four classes correspond to a combination of the classes of cg and c. They are referred to by combining the class labels using a period (.). For example, the combination of class 1 of cg and class 1 of c is referred to as cg#1.c#1. The default estimator for this type of analysis is maximum likelihood with robust standard errors. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. An explanation of the other commands can be found in Example 8.1.
TITLE: this is an example of a LCGA for a binary
outcome
DATA: FILE IS ex8.9.dat;
VARIABLE: NAMES ARE u1-u4;
CLASSES = c (2);
CATEGORICAL = u1-u4;
ANALYSIS: TYPE = MIXTURE;
MODEL:
%OVERALL%
i s | u1@0 u2@1 u3@2 u4@3;
OUTPUT: TECH1 TECH8;
The difference between this example and Example 8.4 is that a LCGA for a binary outcome as shown in the picture above is estimated instead of a GMM. The difference between these two models is that GMM allows within class variability and LCGA does not (Kreuter & Muthén, 2008; Muthén, 2004; Muthén & Asparouhov, 2009).
When TYPE=MIXTURE without ALGORITHM=INTEGRATION is selected, a LCGA is carried out. In the parameterization of the growth model shown here, the thresholds of the outcome variable at the four time points are held equal as the default. The intercept growth factor mean is fixed at zero in the last class and estimated in the other classes. The slope growth factor mean is estimated as the default in all classes. The variances of the growth factors are fixed at zero as the default without ALGORITHM=INTEGRATION. Because of this, the growth factor covariance is fixed at zero. The default estimator for this type of analysis is maximum likelihood with robust standard errors. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. An explanation of the other commands can be found in Examples 8.1 and 8.4.
TITLE: this is an example of a LCGA for a three-category outcome
DATA: FILE IS ex8.10.dat;
VARIABLE: NAMES ARE u1-u4;
CLASSES = c(2);
CATEGORICAL = u1-u4;
ANALYSIS: TYPE = MIXTURE;
MODEL:
%OVERALL%
i s | u1@0 u2@1 u3@2 u4@3;
! [u1$1-u4$1*-.5] (1);
! [u1$2-u4$2* .5] (2);
! %c#1%
! [i*1 s*0];
! %c#2%
! [i@0 s*0];
OUTPUT: TECH1 TECH8;
The difference between this example and Example 8.9 is that the outcome variable is an ordered categorical (ordinal) variable instead of a binary variable. Note that the statements that are commented out are not necessary. This results in an input identical to Example 8.9. The statements are shown to illustrate how starting values can be given for the thresholds and growth factor means in the model if this is needed. Because the outcome is a three-category variable, it has two thresholds. An explanation of the other commands can be found in Examples 8.1, 8.4 and 8.9.
TITLE: this is an example of a LCGA for a count
outcome using a zero-inflated Poisson
model
DATA: FILE IS ex8.11.dat;
VARIABLE: NAMES ARE u1-u4;
COUNT = u1-u4 (i);
CLASSES = c (2);
ANALYSIS: TYPE = MIXTURE;
MODEL:
%OVERALL%
i s | u1@0 u2@1 u3@2 u4@3;
ii si | u1#1@0 u2#1@1 u3#1@2 u4#1@3;
OUTPUT: TECH1 TECH8;
The difference between this example and Example 8.9 is that the outcome variable is a count variable instead of a continuous variable. The COUNT option is used to specify which dependent variables are treated as count variables in the model and its estimation and whether a Poisson or zero-inflated Poisson model will be estimated. In the example above, u1, u2, u3, and u4 are count variables and a zero-inflated Poisson model is used. The count variables represent the outcome measured at four equidistant occasions.
With a zero-inflated Poisson model, two growth models are estimated. The first | statement describes the growth model for the count part of the outcome for individuals who are able to assume values of zero and above. The second | statement describes the growth model for the inflation part of the outcome, the probability of being unable to assume any value except zero. The binary latent inflation variable is referred to by adding to the name of the count variable the number sign (#) followed by the number 1.
In the parameterization of the growth model for the count part of the outcome, the intercepts of the outcome variable at the four time points are fixed at zero as the default. The means of the growth factors are estimated as the default. The variances of the growth factors are fixed at zero. Because of this, the growth factor covariance is fixed at zero as the default. The means of the growth factors are not held equal across classes as the default.
In the parameterization of the growth model for the inflation part of the outcome, the intercepts of the outcome variable at the four time points are held equal as the default. The mean of the intercept growth factor is fixed at zero in all classes as the default. The mean of the slope growth factor is estimated and held equal across classes as the default. These defaults can be overridden, but freeing too many parameters in the inflation part of the model can lead to convergence problems. The variances of the growth factors are fixed at zero. Because of this, the growth factor covariance is fixed at zero. The default estimator for this type of analysis is maximum likelihood with robust standard errors. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. An explanation of the other commands can be found in Examples 8.1 and 8.9.
TITLE: this is an example of a hidden Markov
model with four time points
DATA: FILE IS ex8.12.dat;
VARIABLE: NAMES ARE u1-u4;
CATEGORICAL = u1-u4;
CLASSES = c1(2) c2(2) c3(2) c4(2);
ANALYSIS: TYPE = MIXTURE;
MODEL:
%OVERALL%
[c2#1-c4#1] (1);
c4 ON c3 (2);
c3 ON c2 (2);
c2 ON c1 (2);
MODEL c1:
%c1#1%
[u1$1] (3);
%c1#2%
[u1$1] (4);
MODEL c2:
%c2#1%
[u2$1] (3);
%c2#2%
[u2$1] (4);
MODEL c3:
%c3#1%
[u3$1] (3);
%c3#2%
[u3$1] (4);
MODEL c4:
%c4#1%
[u4$1] (3);
%c4#2%
[u4$1] (4);
OUTPUT: TECH1 TECH8;
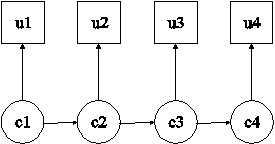
In this example, the hidden Markov model for a single binary outcome measured at four time points shown in the picture above is estimated. Although each categorical latent variable has only one latent class indicator, this model allows the estimation of measurement error by allowing latent class membership and observed response to disagree. This is a first-order Markov process where the transition matrices are specified to be equal over time (Langeheine & van de Pol, 2002). The parameterization of this model is described in Chapter 14.
The CLASSES option is used to assign names to the categorical latent variables in the model and to specify the number of latent classes in the model for each categorical latent variable. In the example above, there are four categorical latent variables c1, c2, c3, and c4. All of the categorical latent variables have two latent classes. In the overall model, the transition matrices are held equal over time. This is done by placing (1) after the bracket statement for the intercepts of c2, c3, and c4 and by placing (2) after each of the ON statements that represent the first-order Markov relationships. When a model has more than one categorical latent variable, MODEL followed by a label is used to describe the analysis model for each categorical latent variable. Labels are defined by using the names of the categorical latent variables. The class-specific equalities (3) and (4) represent measurement invariance across time. An explanation of the other commands can be found in Example 8.1.
TITLE: this is an example of a LTA for two time points with a binary covariate influencing the latent transition probabilities
DATA: FILE = ex8.13.dat;
VARIABLE: NAMES = u11-u15 u21-u25 g;
CATEGORICAL = u11-u15 u21-u25;
CLASSES = cg (2) c1 (3) c2 (3);
KNOWNCLASS = cg (g = 0 g = 1);
ANALYSIS: TYPE = MIXTURE;
MODEL: %OVERALL%
c1 c2 ON cg;
MODEL cg: %cg#1%
c2 ON c1;
%cg#2%
c2 ON c1;
MODEL c1: %c1#1%
[u11$1] (1);
[u12$1] (2);
[u13$1] (3);
[u14$1] (4);
[u15$1] (5);
%c1#2%
[u11$1] (6);
[u12$1] (7);
[u13$1] (8);
[u14$1] (9);
[u15$1] (10);
%c1#3%
[u11$1] (11);
[u12$1] (12);
[u13$1] (13);
[u14$1] (14);
[u15$1] (15);
MODEL c2:
%c2#1%
[u21$1] (1);
[u22$1] (2);
[u23$1] (3);
[u24$1] (4);
[u25$1] (5);
%c2#2%
[u21$1] (6);
[u22$1] (7);
[u23$1] (8);
[u24$1] (9);
[u25$1] (10);
%c2#3%
[u21$1] (11);
[u22$1] (12);
[u23$1] (13);
[u24$1] (14);
[u25$1] (15);
OUTPUT: TECH1 TECH8 TECH15;
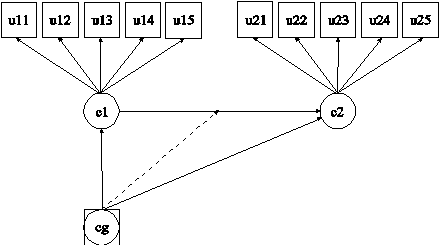
In this example, the latent transition analysis (LTA; Mooijaart, 1998; Reboussin et al., 1998; Kaplan, 2007; Nylund, 2007; Collins & Lanza, 2010) model for two time points with a binary covariate influencing the latent transition probabilities shown in the picture above is estimated. The same five latent class indicators are measured at two time points. The model assumes measurement invariance across time for the five latent class indicators. The parameterization of this model is described in Chapter 14.
The KNOWNCLASS option is used for multiple group analysis with TYPE=MIXTURE to identify the categorical latent variable for which latent class membership is known and is equal to observed groups in the sample. The KNOWNCLASS option identifies cg as the categorical latent variable for which class membership is known. The information in parentheses following the categorical latent variable name defines the known classes using an observed variable. In this example, the observed variable g is used to define the known classes. The first class consists of individuals with the value 0 on the variable g. The second class consists of individuals with the value 1 on the variable g.
In the overall model, the first ON statement describes the multinomial logistic regression of the categorical latent variables c1 and c2 on the known class variable cg. This allows the class probabilities to vary across the observed groups in the sample.
When there are multiple categorical latent variables, each one has its own MODEL command. The MODEL command for each categorical latent variable is specified by MODEL followed by the name of the categorical latent variable. In this example, MODEL cg describes the group-specific parameters of the regression of c2 on c1. This allows the binary covariate to influence the latent transition probabilities. MODEL c1 describes the class-specific measurement parameters for variable c1 and MODEL c2 describes the class-specific measurement parameters for variable c2. The model for each categorical latent variable that differs for each class of that variable is specified by a label that consists of the categorical latent variable name followed by the number sign followed by the class number. For example, in the example above, the label %c1#1% refers to class 1 of categorical latent variable c1.
In this example, the thresholds of the latent class indicators for a given class are held equal for the two categorical latent variables. The (1-5), (6-10), and (11-15) following the bracket statements containing the thresholds use the list function to assign equality labels to these parameters. For example, the label 1 is assigned to the thresholds u11$1 and u21$1 which holds these thresholds equal over time.
The TECH15 option is used to obtain the transition probabilities for each of the two known classes. The default estimator for this type of analysis is maximum likelihood with robust standard errors. The estimator option of the ANALYSIS command can be used to select a different estimator. An explanation of the other commands can be found in Example 8.1.
Following is the second part of the example that shows an alternative parameterization. The PARAMETERIZATION option is used to select a probability parameterization rather than a logit parameterization. This allows latent transition probabilities to be expressed directly in terms of probability parameters instead of via logit parameters. In the overall model, only the c1 on cg regression is specified, not the c2 on cg regression. Other specifications are the same as in the first part of the example.
ANALYSIS: TYPE = MIXTURE;
PARAMETERIZATION = PROBABILITY;
MODEL: %OVERALL%
c1 ON cg;
MODEL cg: %cg#1%
c2 ON c1;
%cg#2%
c2 ON c1;
TITLE: this is an example of a LTA for two time points with a continuous covariate influencing the latent transition probabilities
DATA: FILE = ex8.14.dat;
VARIABLE: NAMES = u11-u15 u21-u25 x;
CATEGORICAL = u11-u15 u21-u25;
CLASSES = c1 (3) c2 (3);
ANALYSIS: TYPE = MIXTURE;
PROCESSORS = 8;
MODEL: %OVERALL%
c1 ON x;
c2 ON c1;
MODEL c1: %c1#1%
c2 ON x;
[u11$1] (1);
[u12$1] (2);
[u13$1] (3);
[u14$1] (4);
[u15$1] (5);
%c1#2%
c2 ON x;
[u11$1] (6);
[u12$1] (7);
[u13$1] (8);
[u14$1] (9);
[u15$1] (10);
%c1#3%
c2 ON x;
[u11$1] (11);
[u12$1] (12);
[u13$1] (13);
[u14$1] (14);
[u15$1] (15);
MODEL c2: %c2#1%
[u21$1] (1);
[u22$1] (2);
[u23$1] (3);
[u24$1] (4);
[u25$1] (5);
%c2#2%
[u21$1] (6);
[u22$1] (7);
[u23$1] (8);
[u24$1] (9);
[u25$1] (10);
%c2#3%
[u21$1] (11);
[u22$1] (12);
[u23$1] (13);
[u24$1] (14);
[u25$1] (15);
OUTPUT: TECH1 TECH8;
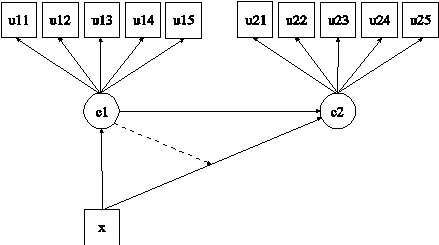
In this example, the latent transition analysis (LTA; Reboussin et al., 1998; Kaplan, 2007; Nylund, 2007; Collins & Lanza, 2010) model for two time points with a continuous covariate influencing the latent transition probabilities shown in the picture above is estimated. The same five latent class indicators are measured at two time points. The model assumes measurement invariance across time for the five latent class indicators. The parameterization of this model is described in Chapter 14.
In the overall model, the first ON statement describes the multinomial logistic regression of the categorical latent variable c1 on the continuous covariate x. The second ON statement describes the multinomial logistic regression of c2 on c1. The multinomial logistic regression of c2 on the continuous covariate x is specified in the class-specific parts of MODEL c1. This follows parameterization 2 discussed in Muthén and Asparouhov (2011). The class-specific regressions of c2 on x allow the continuous covariate x to influence the latent transition probabilities. The latent transition probabilities for different values of the covariates can be computed by choosing LTA calculator from the Mplus menu of the Mplus Editor.
When there are multiple categorical latent variables, each one has its own MODEL command. The MODEL command for each categorical latent variable is specified by MODEL followed by the name of the categorical latent variable. MODEL c1 describes the class-specific multinomial logistic regression of c2 on x and the class-specific measurement parameters for variable c1. MODEL c2 describes the class-specific measurement parameters for variable c2. The model for each categorical latent variable that differs for each class of that variable is specified by a label that consists of the categorical latent variable name followed by the number sign followed by the class number. For example, in the example above, the label %c1#1% refers to class 1 of categorical latent variable c1.
In this example, the thresholds of the latent class indicators for a given class are held equal for the two categorical latent variables. The (1-5), (6-10), and (11-15) following the bracket statements containing the thresholds use the list function to assign equality labels to these parameters. For example, the label 1 is assigned to the thresholds u11$1 and u21$1 which holds these thresholds equal over time. The default estimator for this type of analysis is maximum likelihood with robust standard errors. The estimator option of the ANALYSIS command can be used to select a different estimator. An explanation of the other commands can be found in Example 8.1.
TITLE: this is an example of a mover-stayer LTA for three time points using a probability parameterization
DATA: FILE = ex8.15.dat;
VARIABLE: NAMES = u11-u15 u21-u25 u31-u35;
CATEGORICAL = u11-u15 u21-u25 u31-u35;
CLASSES = c(2) c1(3) c2(3) c3(3);
ANALYSIS: TYPE = MIXTURE;
PARAMETERIZATION = PROBABILITY;
STARTS = 100 20;
PROCESSORS = 8;
MODEL: %OVERALL%
c1 ON c;
MODEL c: %c#1% !mover class
c2 ON c1;
c3 ON c2;
%c#2% ! stayer class
c2#1 ON c1#1@1; c2#2 ON c1#1@0;
c2#1 ON c1#2@0; c2#2 ON c1#2@1;
c2#1 ON c1#3@0; c2#2 ON c1#3@0;
c3#1 ON c2#1@1; c3#2 ON c2#1@0;
c3#1 ON c2#2@0; c3#2 ON c2#2@1;
c3#1 ON c2#3@0; c3#2 ON c2#3@0;
MODEL c1: %c1#1%
[u11$1] (1);
[u12$1] (2);
[u13$1] (3);
[u14$1] (4);
[u15$1] (5);
%c1#2%
[u11$1] (6);
[u12$1] (7);
[u13$1] (8);
[u14$1] (9);
[u15$1] (10);
%c1#3%
[u11$1] (11);
[u12$1] (12);
[u13$1] (13);
[u14$1] (14);
[u15$1] (15);
MODEL c2:
%c2#1%
[u21$1] (1);
[u22$1] (2);
[u23$1] (3);
[u24$1] (4);
[u25$1] (5);
%c2#2%
[u21$1] (6);
[u22$1] (7);
[u23$1] (8);
[u24$1] (9);
[u25$1] (10);
%c2#3%
[u21$1] (11);
[u22$1] (12);
[u23$1] (13);
[u24$1] (14);
[u25$1] (15);
MODEL c3:
%c3#1%
[u31$1] (1);
[u32$1] (2);
[u33$1] (3);
[u34$1] (4);
[u35$1] (5);
%c3#2%
[u31$1] (6);
[u32$1] (7);
[u33$1] (8);
[u34$1] (9);
[u35$1] (10);
%c3#3%
[u31$1] (11);
[u32$1] (12);
[u33$1] (13);
[u34$1] (14);
[u35$1] (15);
OUTPUT: TECH1 TECH8 TECH15;
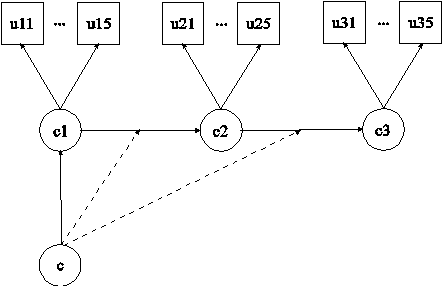
In this example, the mover-stayer (Langeheine & van de Pol, 2002) latent transition analysis (LTA) for three time points using a probability parameterization shown in the picture above is estimated. The same five latent class indicators are measured at three time points. The model assumes measurement invariance across time for the five latent class indicators. The parameterization of this model is described in Chapter 14.
The PARAMETERIZATION option is used to select a probability parameterization rather than a logit parameterization. This allows latent transition probabilities to be expressed directly in terms of probability parameters instead of via logit parameters. The alternative logit parameterization of mover-stayer LTA is described in the document LTA With Movers-Stayers (see FAQ, www.statmodel.com).
In the overall model, the ON statement describes the multinomial logistic regression of the categorical latent variable c1 on the mover-stayer categorical latent variable c. The multinomial logistic regressions of c2 on c1 and c3 on c2 are specified in the class-specific parts of MODEL c.
When there are multiple categorical latent variables, each one has its own MODEL command. The MODEL command for each categorical latent variable is specified by MODEL followed by the name of the categorical latent variable. MODEL c describes the class-specific multinomial logistic regressions of c2 on c1 and c3 on c2 where the first c class is the mover class and the second c class is the stayer class. MODEL c1 describes the class-specific measurement parameters for variable c1; MODEL c2 describes the class-specific measurement parameters for variable c2; and MODEL c3 describes the class-specific measurement parameters for variable c3. The model for each categorical latent variable that differs for each class of that variable is specified by a label that consists of the categorical latent variable name followed by the number sign followed by the class number. For example, in the example above, the label %c1#1% refers to class 1 of categorical latent variable c1.
In class 1, the mover class of MODEL c, the two ON statements specify that the latent transition probabilities are estimated. In class 2, the stayer class, the ON statements specify that the latent transition probabilities are fixed at either zero or one. A latent transition probability of one specifies that an observation stays in the same class across time.
In this example, the thresholds of the latent class indicators for a given class are held equal for the three categorical latent variables. The (1-5), (6-10), and (11-15) following the bracket statements containing the thresholds use the list function to assign equality labels to these parameters. For example, the label 1 is assigned to the thresholds u11$1, u21$1, and u31$1 which holds these thresholds equal over time.
The TECH15 option is used to obtain the transition probabilities for both the mover and stayer classes. The default estimator for this type of analysis is maximum likelihood with robust standard errors. The estimator option of the ANALYSIS command can be used to select a different estimator. An explanation of the other commands can be found in Example 8.1.
EXAMPLE 8.16: DISCRETE-TIME SURVIVAL MIXTURE ANALYSIS WITH SURVIVAL PREDICTED BY GROWTH TRAJECTORY CLASSES
TITLE: this is an example of a discrete-time survival mixture analysis with survival predicted by growth trajectory classes
DATA: FILE IS ex8.16.dat;
VARIABLE: NAMES ARE y1-y3 u1-u4;
CLASSES = c(2);
CATEGORICAL = u1-u4;
MISSING = u1-u4 (999);
ANALYSIS: TYPE = MIXTURE;
MODEL:
%OVERALL%
i s | y1@0 y2@1 y3@2;
f BY u1-u4@1;
OUTPUT: TECH1 TECH8;
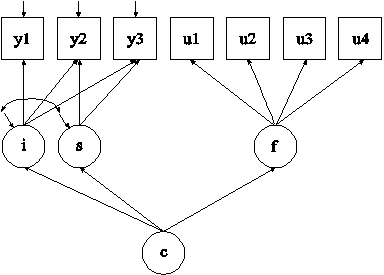
In this example, the discrete-time survival mixture analysis model shown in the picture above is estimated. In this model, a survival model for u1, u2, u3, and u4 is specified for each class of c defined by a growth mixture model for y1-y3 (Muthén & Masyn, 2005). Each u variable represents whether or not a single non-repeatable event has occurred in a specific time period. The value 1 means that the event has occurred, 0 means that the event has not occurred, and a missing value flag means that the event has occurred in a preceding time period or that the individual has dropped out of the study. The factor f is used to specify a proportional odds assumption for the hazards of the event. The arrows from c to the growth factors i and s indicate that the means of the growth factors vary across the classes of c.
In the overall model, the | symbol is used to name and define the intercept and slope growth factors in a growth model. The names i and s on the left-hand side of the | symbol are the names of the intercept and slope growth factors, respectively. The statement on the right-hand side of the | symbol specifies the outcomes and the time scores for the growth model. The time scores for the slope growth factor are fixed at 0, 1, and 2 to define a linear growth model with equidistant time points. The zero time score for the slope growth factor at time point one defines the intercept growth factor as an initial status factor. The coefficients of the intercept growth factor are fixed at one as part of the growth model parameterization. The residual variances of the outcome variables are estimated and allowed to be different across time and the residuals are not correlated as the default.
In the parameterization of the growth model shown here, the intercepts of the outcome variable at the four time points are fixed at zero as the default. The means and variances of the growth factors are estimated as the default, and the growth factor covariance is estimated as the default because they are independent (exogenous) variables. The means of the growth factors are not held equal across classes as the default. The variances and covariance of the growth factors are held equal across classes as the default.
In the overall model, the BY statement specifies that f is measured by u1, u2, u3, and u4 where the factor loadings are fixed at one. This represents a proportional odds assumption. The mean of f is fixed at zero in class two as the default. The variance of f is fixed at zero in both classes. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. An explanation of the other commands can be found in Example 8.1.
TITLE: this is an example of a continuous-time survival mixture analysis using a Cox regression model
DATA: FILE = ex8.17.dat;
VARIABLE: NAMES = t u1-u5 x tc;
CATEGORICAL = u1-u5;
CLASSES = c (2);
SURVIVAL = t (ALL);
TIMECENSORED = tc (0 = NOT 1 = RIGHT);
ANALYSIS: TYPE = MIXTURE;
MODEL: %OVERALL%
t ON x;
c ON x;
%c#1%
[u1$1-u5$1];
t ON x;
%c#2%
[u1$1-u5$1];
t ON x;
OUTPUT: TECH1 TECH8;

In this example, the continuous-time survival analysis model shown in the picture above is estimated. This is a Cox regression mixture model similar to the model of Larsen (2004) as discussed in Asparouhov et al. (2006). The profile likelihood method is used for estimation.
The SURVIVAL option is used to identify the variables that contain information about time to event and to provide information about the number and lengths of the time intervals in the baseline hazard function to be used in the analysis. The SURVIVAL option must be used in conjunction with the TIMECENSORED option. In this example, t is the variable that contains time-to-event information. By specifying the keyword ALL in parenthesis following the time-to-event variable, the time intervals are taken from the data. The TIMECENSORED option is used to identify the variables that contain information about right censoring. In this example, the variable is named tc. The information in parentheses specifies that the value zero represents no censoring and the value one represents right censoring. This is the default.
In the overall model, the first ON statement describes the loglinear regression of the time-to-event variable t on the covariate x. The second ON statement describes the multinomial logistic regression of the categorical latent variable c on the covariate x. In the class-specific models, by specifying the thresholds of the latent class indicator variables and the regression of the time-to-event t on the covariate x, these parameters will be estimated separately for each class. The non-parametric baseline hazard function varies across class as the default. The default estimator for this type of analysis is maximum likelihood with robust standard errors. The estimator option of the ANALYSIS command can be used to select a different estimator. An explanation of the other commands can be found in Example 8.1.