CHAPTER 15
TITLE, DATA, VARIABLE, AND DEFINE COMMANDS
In this chapter, the TITLE, DATA, VARIABLE, and DEFINE commands are discussed. The TITLE command is used to provide a title for the analysis. The DATA command is used to provide information about the data set to be analyzed. The VARIABLE command is used to provide information about the variables in the data set to be analyzed. The DEFINE command is used to transform existing variables and create new variables.
The TITLE command is used to provide a title for the analysis. Following is the general format for the TITLE command:
|
TITLE: |
title for the analysis |
|
The TITLE command is not a required command. Note that commands can be shortened to four or more letters.
The TITLE command can contain any letters and symbols except the words used as Mplus commands when they are followed by a colon. These words are: title, data, variable, define, analysis, model, output, savedata, montecarlo, and plot. These words can be included in the title if they are not followed by a colon. Colons can be used in the title as long as they do not follow words that are used as Mplus commands. Following is an example of how to specify a title:
TITLE: confirmatory factor analysis of diagnostic criteria
The title is printed in the output just before the Summary of Analysis.
The DATA command is used to provide information about the data set to be analyzed. The DATA command has options for specifying the location of the data set to be analyzed, describing the format and type of data in the data set, specifying the number of observations and number of groups in the data set if the data are in summary form such as a correlation or covariance matrix, requesting listwise deletion of observations with missing data, and specifying whether the data should be checked for variances of zero.
Data must be numeric except for certain missing value flags and must reside in an external ASCII file. There is no limit on the number of variables or observations. The maximum record length is 10,000. Special features of the DATA command for multiple group analysis are discussed in Chapter 14. Monte Carlo data generation is discussed in Chapters 12 and 19. The estimator chosen for an analysis determines the type of data required for the analysis. Some estimators require a data set with information for each observation. Some estimators require only summary information.
There are six DATA transformation commands. They are used to rearrange data from a wide to long format, to rearrange data from a long to wide format, to create a binary and a continuous variable from a semicontinuous variable, to create a set of binary variables that are indicators of missing data, to create variables for discrete-time survival modeling, and to rearrange longitudinal data from a format where time points represent measurement occasions to a format where time points represent age or another time-related variable.
Following are the options for the DATA and the DATA transformation commands:
|
DATA: |
|
|
|
FILE IS |
file name; |
|
|
FORMAT IS |
format statement; |
FREE |
|
|
FREE; |
|
|
TYPE IS |
INDIVIDUAL; |
INDIVIDUAL |
|
|
COVARIANCE; |
|
|
|
CORRELATION; |
|
|
|
FULLCOV; |
|
|
|
FULLCORR; |
|
|
|
MEANS; |
|
|
|
STDEVIATIONS; |
|
|
|
MONTECARLO; |
|
|
|
IMPUTATION; |
|
|
NOBSERVATIONS ARE |
number of observations; |
|
|
NGROUPS = |
number of groups; |
1 |
|
LISTWISE = |
ON; OFF; |
OFF |
|
SWMATRIX = |
file name; |
|
|
VARIANCES = |
CHECK; NOCHECK; |
CHECK |
|
DATA IMPUTATION: IMPUTE =
NDATASETS = SAVE =
FORMAT = MODEL =
VALUES = ROUNDING =
THIN = |
names of variables for which missing values will be imputed; number of imputed data sets; names of files in which imputed data sets are stored; format statement; COVARIANCE; SEQUENTIAL; REGRESSION; values imputed data can take; number of decimals for imputed continuous variables; k where every k-th imputation is saved; |
5
F10.3 depends on analysis type
no restrictions 3
100 |
|
DATA WIDETOLONG: WIDE = LONG = IDVARIABLE = REPETITION = |
names of old wide format variables; names of new long format variables; name of variable with ID information; name of variable with repetition information; |
ID REP |
|
DATA LONGTOWIDE: LONG = WIDE = IDVARIABLE = REPETITION = |
names of old long format variables; names of new wide format variables; name of variable with ID information; name of variable with repetition information (values); |
0, 1, 2, etc. |
|
DATA TWOPART: NAMES =
CUTPOINT =
BINARY = CONTINUOUS = TRANSFORM = |
names of variables used to create a set of binary and continuous variables; value used to divide the original variables into a set of binary and continuous variables; names of new binary variables; names of new continuous variables; function to use to transform new continuous variables; |
0
LOG |
|
DATA MISSING: NAMES =
BINARY = |
names of variables used to create a set of binary variables; names of new binary variables; |
|
|
TYPE = |
MISSING; SDROPOUT; DDROPOUT; |
|
|
DESCRIPTIVE = |
sets of variables for additional descriptive statistics separated by the | symbol; |
|
|
DATA SURVIVAL: NAMES =
CUTPOINT =
BINARY = |
names of variables used to create a set of binary event-history variables; value used to create a set of binary event-history variables from a set of original variables; names of new binary variables; |
|
|
DATA COHORT: COHORT IS COPATTERN IS COHRECODE = TIMEMEASURES =
TNAMES = |
name of cohort variable (values); name of cohort/pattern variable (patterns); (old value = new value); list of sets of variables separated by the | symbol; list of root names for the sets of variables in TIMEMEASURES separated by the | symbol; |
|
The DATA command is a required command. The FILE option is a required option. The NOBSERVATIONS option is required when summary data are analyzed. This option is not required when individual data are analyzed. Default settings are shown in the last column. If the default settings are appropriate for the options that are not required, nothing needs to be specified for these options.
Note that commands and options can be shortened to four or more letters. Option settings can be referred to by either the complete word or the part of the word shown above in bold type.
The FILE option is used to specify the name and location of the ASCII file that contains the data to be analyzed. The FILE option is required for each analysis. It is specified for a single group analysis as follows:
FILE IS c:\analysis\data.dat;
where data.dat is the name of the ASCII file containing the data to be analyzed. In this example, the file data.dat is located in the directory c:\analysis. If the full path name of the data set contains any blanks, the full path name must have quotes around it.
If the name of the data set is specified with a path, the directory specified by the path is checked. If the name of the data set is specified without a path, the local directory is checked. If the data set is not found in the local directory, the directory where the input file is located is checked.
The FORMAT option is used to describe the format of the data set to be analyzed. Individual data can be in fixed or free format. Free format is the default. Fixed format is recommended for large data sets because it is faster to read data using a fixed format. Summary data must be in free format.
For data in free format, each entry on a record must be delimited by a comma, space, or tab. When data are in free format, the use of blanks is not allowed. The number of variables in the data set is determined from information provided in the NAMES option of the VARIABLE command. Data are read until the number of pieces of information equal to the number of variables is found. The program then goes to the next record to begin reading information for the next observation.
For data in fixed format, each observation must have the same number of records. Information for a given variable must occupy the same position on the same record for each observation. A FORTRAN-like format statement describing the position of the variables in the data set is required. Following is an example of how to specify a format statement:
FORMAT IS 5F4.0, 10x, 6F1.0;
Although any FORTRAN format descriptor (i.e., F, I, G, E, x, t, /, etc.) is acceptable in a format statement, most format statements use only F, t, x, and /. Following is an explanation of how to create a FORTRAN-like format statement using these descriptors.
The F format describes the format for a real variable. F is followed by a number. It can be a whole number or a decimal, for example, F5.3. The number before the decimal point describes the number of columns reserved for the variable; the number after the decimal point specifies the number of decimal places. If the number 34234 is read with an F5.3 format, it is read as 34.234. If the data contain a decimal point, it is not necessary to specify information about the position of the decimal point. For example, the number 34.234 can be read with a F6 format as 34.234.
The F format can also be preceded by a number. This number represents the number of variables to be read using that format. The statement 5F5.3 is a shorthand way of saying F5.3, F5.3, F5.3, F5.3, F5.3.
There are three options for the format statement related to skipping columns or records when reading data: x, t, and /. The x option instructs the program to skip columns. The statement 10x says to skip 10 columns and begin reading in column 11. The t option instructs the program to go to a particular column and begin reading. For example, t130 says to go to column 130 and begin reading in column 130. The / option is used to instruct the program to go to the next record. Consider the following format statements:
1. (20F4, 13F5, 3F2)
2. (3F4.1,25x,5F5)
3. (3F4.1,t38,5F5)
4. (2F4/14F4.2//6F3.1)
1. In the first statement, for each record the program reads 20 four-digit numbers followed by 13 five-digit numbers, then three two-digit numbers with a total record length of 151.
2. In the second statement, for each record the program reads three four-digit numbers with one digit to the right of the decimal, skips 25 spaces, and then reads five five-digit numbers with a total record length of 62.
3. The third statement is the same as the second but uses the t option instead of the x option. In the third statement, for each record the program reads three four-digit numbers with one digit to the right of the decimal, goes to column 38, and then reads five five-digit numbers.
4. In the fourth statement, each observation has four records. For record one the program reads two four-digit numbers; for record two the program reads fourteen four-digit numbers with two digits to the right of the decimal; record three is skipped; and for record four the program reads six three-digit numbers with one number to the right of the decimal point.
Following is an example of a data set with six one-digit numbers with no numbers to the right of the decimal point:
123234
342765
348765
The format statement for the data set above is:
FORMAT IS 6F1.0;
or
FORMAT IS 6F1;
The TYPE option is used in conjunction with the FILE option to describe the contents of the file named using the FILE option. It has the following settings:
INDIVIDUAL Data matrix where rows represent observations and columns represent variables
COVARIANCE A lower triangular covariance matrix read row wise
CORRELATION A lower triangular correlation matrix read row wise
FULLCOV A full covariance matrix read row wise
FULLCORR A full correlation matrix read row wise
MEANS Means
STDEVIATIONS Standard deviations
MONTECARLO A list of the names of the data sets to be analyzed
IMPUTATION A list of the names of the imputed data sets to be analyzed
The default for the TYPE option is INDIVIDUAL. The TYPE option is not required if individual data are being analyzed where rows represent observations and columns represent variables.
The TYPE option is required when summary data such as a covariance matrix or a correlation matrix are analyzed. The TYPE option has six settings related to the analysis of summary data. They are: COVARIANCE, CORRELATION, FULLCOV, FULLCORR, MEANS, and STDEVIATIONS. Summary data must reside in a free format external ASCII file. The number of observations must be specified using the NOBSERVATIONS option of the DATA command.
When summary data are analyzed and one or more dependent
variables are binary or ordered categorical (ordinal), only a correlation
matrix can be analyzed. When summary data are analyzed and all dependent
variables are continuous, a covariance matrix is usually analyzed. In some
cases, a correlation matrix can be analyzed.
A data set with all continuous dependent variables in the form of a correlation matrix, standard deviations, and means is specified as:
TYPE IS CORRELATION MEANS STDEVIATIONS;
The program creates a covariance matrix using the correlations and standard deviations and then analyzes the means and covariance matrix.
The external ASCII file for the above example contains the means, standard deviations, and correlations in free format. Each type of data must begin on a separate record even if the data fits on less than one record. The means come first; the standard deviations begin on the record following the last mean; and the entries of the lower triangular correlation matrix begin on the record following the last standard deviation. The data set appears as follows:
.4 .6 .3 .5 .5
.2 .5 .4 .5 .6
1.0
.86 1.0
.56 .76 1.0
.78 .34 .48 1.0
.65 .87 .32 .56 1.0
or alternatively:
.4 .6 .3 .5 .5
.2 .5 .4 .5 .6
1.0 .86 1.0 .56 .76 1.0 .78 .34 .48 1.0 .65 .87 .32 .56 1.0
The MONTECARLO setting of the TYPE option is used when the data sets being analyzed have been generated and saved using either the REPSAVE option of the MONTECARLO command or by another computer program. The file named using the FILE option of the DATA command contains a list of the names of the data sets to be analyzed and summarized as in a Monte Carlo study. This ASCII file is created automatically when the data sets are generated and saved in a prior analysis using the REPSAVE option of the MONTECARLO command. This file must be created by the user when the data sets are generated and saved using another computer program. Each record of the file must contain one data set name. For example, if five data sets are being analyzed, the contents of the file would be:
data1.dat
data2.dat
data3.dat
data4.dat
data5.dat
where data1.dat, data2.dat, data3.dat, data4.dat, and data5.dat are the names of the five data sets generated and saved using another computer program. All files must be in the same format. Files saved using the REPSAVE option are in free format.
When the MONTECARLO option is used, the results are presented in a Monte Carlo summary format. The output includes the population value for each parameter, the average of the parameter estimates across replications, the standard deviation of the parameter estimates across replications, the average of the estimated standard errors across replications, the mean square error for each parameter (M.S.E.), 95 percent coverage, and the proportion of replications for which the null hypothesis that a parameter is equal to zero is rejected at the .05 level. In addition, the average fit statistics and the percentiles for the fit statistics are given if appropriate. A description of Monte Carlo output is given in Chapter 12.
The IMPUTATION setting of the TYPE option is used when the data sets being analyzed have been generated using multiple imputation procedures. The file named using the FILE option of the DATA command must contain a list of the names of the multiple imputation data sets to be analyzed. Parameter estimates are averaged over the set of analyses. Standard errors are computed using the average of the squared standard errors over the set of analyses and the between analysis parameter estimate variation (Rubin, 1987; Schafer, 1997). A chi-square test of overall model fit is provided (Asparouhov & Muthén, 2008c; Enders, 2010). The ASCII file containing the names of the data sets must be created by the user. Each record of the file must contain one data set name. For example, if five data sets are being analyzed, the contents of the file would be:
imp1.dat
imp2.dat
imp3.dat
imp4.dat
imp5.dat
where imp1.dat, imp2.dat, imp3.dat, imp4.dat, and imp5.dat are the names of the five data sets created using multiple imputation.
The NOBSERVATIONS option is required when summary data are analyzed. When individual data are analyzed, the program counts the number of observations. The NOBSERVATIONS option can, however, be used with individual data to limit the number of records used in the analysis. For example, if a data set contains 20,000 observations, it is possible to analyze only the first 1,000 observations by specifying:
NOBSERVATIONS = 1000;
The NGROUPS option is used for multiple group analysis when summary data are analyzed. It specifies the number of groups in the analysis. It is specified as follows:
NGROUPS = 3;
which indicates that the analysis is a three-group analysis. Multiple group analysis is discussed in Chapter 14.
The LISTWISE option is used to indicate that any observation with one or more missing values on the set of analysis variables not be used in the analysis. The default is to estimate the model under missing data theory using all available data. To turn on listwise deletion, specify:
LISTWISE = ON;
The SWMATRIX option is used with TYPE=TWOLEVEL and weighted least squares estimation to specify the name and location of the file that contains the within- and between-level sample statistics and their corresponding estimated asymptotic covariance matrix. The univariate and bivariate sample statistics are estimated using one- and two-dimensional numerical integration with a default of 7 integration points. The INTEGRATION option of the ANALYSIS command can be used to change the default. It is recommended to save this information and use it in subsequent analyses along with the raw data to reduce computational time during model estimation. Analyses using this information must have the same set of observed dependent and independent variables, the same DEFINE command, the same USEOBSERVATIONS statement, and the same USEVARIABLES statement as the analysis which was used to save the information. It is specified as follows:
SWMATRIX = swmatrix.dat;
where swmatrix.dat is the file that contains the within- and between-level sample statistics and their corresponding estimated asymptotic covariance matrix.
For TYPE=IMPUTATION, the file specified contains a list of file names. These files contain the within- and between-level sample statistics and their corresponding estimated asymptotic covariance matrix for a set of imputed data sets.
The VARIANCES option is used to check that the analysis variables do not have variances of zero in the sample used for the analysis. Checking for variances of zero is the default. To turn off this check, specify:
VARIANCES = NOCHECK;
The DATA IMPUTATION command is used when a data set contains missing values to create a set of imputed data sets using multiple imputation methodology. Imputation refers to the estimation of missing values in a data set to create a data set without missing values. Multiple imputation refers to the creation of several data sets where missing values have been imputed. Multiple imputation is carried out using Bayesian estimation. The multiple imputations are random draws from the posterior distribution of the missing values (Rubin, 1987; Schafer, 1997). For an overview, see Enders (2010). The multiple imputation data sets can be used for subsequent model estimation using maximum likelihood or weighted least squares estimation of each data set where the parameter estimates are averaged over the data sets and the standard errors are computed using the Rubin formula (Rubin, 1987). A chi-square test of overall model fit is provided (Asparouhov & Muthén, 2008c; Enders, 2010). Plausible values for latent variables in the model can be saved by specifying SAVE=FSCORES in conjunction with the FACTORS option of the SAVEDATA command.
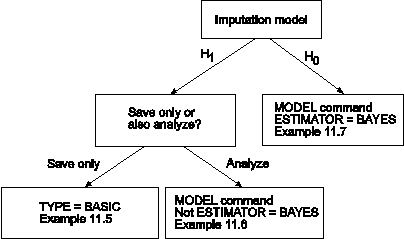
The figure above shows three ways that data imputation can be done. The first path in the figure uses an unrestricted H1 imputation model and saves the imputed data sets for a subsequent analysis. In this case, TYPE=BASIC is specified in the ANALYSIS command. See Example 11.5. To use the data sets in a subsequent analysis, specify TYPE=IMPUTATION in the DATA command. See Example 13.13. The second path in the figure uses an unrestricted H1 imputation model with an estimator other than BAYES. In this case, the model is estimated immediately after the data are imputed. See Example 11.6. The third path in the figure uses an H0 imputation model and ESTIMATOR=BAYES. The H0 model specified in the MODEL command is used to impute the data. See Example 11.7.
IMPUTE
The IMPUTE option is used to specify the analysis variables for which missing values will be imputed. Data can be imputed for all or a subset of the analysis variables. These variables can be continuous or categorical. If they are categorical a letter c in parentheses must be included after the variable name. If a variable is on the CATEGORICAL list in the VARIABLE command, it must have a c in parentheses following its name. A variable not on the CATEGORICAL list can have a c in parentheses following its name. Following is an example of how to specify the IMPUTE option:
IMPUTE = y1-y4 u1-u4 (c) x1 x2;
where values will be imputed for the continuous variables y1, y2, y3, y4, x1, and x2 and the categorical variables u1, u2, u3, and u4.
The IMPUTE option has an alternative specification that is convenient when there are several variables that cannot be specified using the list function. When c in parentheses follows the equal sign, it means that c applies to all of the variables that follow. For example, the following IMPUTE statement specifies that the variables x1, x3, x5, x7, and x9 are categorical:
IMPUTE = (c) x1 x3 x5 x7 x9;
The keyword ALL can be used to indicate that values are to be imputed for all variables in the dataset. The ALL option can be used with the c setting, for example,
IMPUTE = ALL (c);
indicates that all of the variables in the data set are categorical.
The NDATASETS option is used to specify the number of imputed data sets to create. The default is five. Following is an example of how to specify the NDATASETS option:
NDATASETS = 20;
where 20 is the number of imputed data sets that will be created. The default for the NDATASETS option is 5.
The SAVE option is used to save the imputed data sets for subsequent analysis using TYPE=IMPUTATION in the DATA command. It is specified as follows:
SAVE = impute*.dat;
where the asterisk (*) is replaced by the number of the imputed data set. A file is also produced that contains the names of all of the data sets. To name this file, the asterisk (*) is replaced by the word list.
The FORMAT option is used to specify the format in which the imputed data will be saved. All dependent and independent variables used in the analysis are saved. In addition, all other variables that are used in conjunction with the analysis are saved as well as any variables specified using the AUXILIARY option of the VARIABLE command. The names of the data sets along with the names of the variables saved and the format are printed in the output. The default is to save the analysis variables using a fixed format.
Following is an example of how to specify the FORMAT option to save imputed data in a free format:
FORMAT IS FREE;
Imputed data can also be saved in a fixed format specified by the user. The user has the choice of which F or E format the analysis variables are saved in with the format of other saved variables determined by the program. This option is specified as:
FORMAT IS F2.0;
which indicates that all analysis variables will be saved with an F2.0 format.
MODEL
The MODEL option is used to specify the type of unrestricted H1 model to use for imputation (Asparouhov & Muthén, 2010b). The MODEL option has three settings: COVARIANCE, SEQUENTIAL, and REGRESSION. The default is COVARIANCE. The COVARIANCE setting uses a model of unrestricted means, variances, and covariances for a set of continuous variables. The SEQUENTIAL setting uses a sequential regression method also referred to as the chained equations algorithm in line with Raghunathan et al. (2001). The REGRESSION setting uses a model where variables with missing data are regressed on variables without missing data (Asparouhov & Muthén, 2010b). To request the sequential regression method, specify:
MODEL = SEQUENTIAL;
The VALUES option is used to provide the values for continuous variables that the imputed data can take. The default is to put no restrictions on the values that the imputed data can take. The values must be integers. For example, four five-category variables not declared as categorical can be restricted to take on only the values of one through five by specifying:
VALUES = y1-y4 (1-5);
The closest value to the imputed value is used. If the imputed value is 2.7, the value 3 will be used.
The ROUNDING option is used to specify the number of decimals that imputed continuous variables will have. The default is three. To request that five decimals be used, specify:
ROUNDING = y1-y10 (5);
The value zero is used to specify no decimals, that is, integer values.
The THIN option is used to specify which intervals in the draws from the posterior distribution are used for imputed values. The default is to use every 100th iteration. To request that every 200th iteration be used, specify:
THIN = 200;
There are six DATA transformation commands. They are used to rearrange data from a wide to long format, to rearrange data from a long to wide format, to create a binary and a continuous variable from a semicontinuous variable, to create a set of binary variables that are indicators of missing data for another set of variables, to create variables for discrete-time survival modeling where a binary variable represents the occurrence of a single non-repeatable event, and to rearrange longitudinal data from a format where time points represent measurement occasions to a format where time points represent age or another time-related variable. The DATA transformation commands are executed after the statements in the DEFINE command that come before the CLUSTER_MEAN, CENTER, and STANDARDIZE options of the DEFINE command. The CLUSTER_MEAN, CENTER, and STANDARDIZE options are then executed in the order mentioned followed by the execution of any statements that follow them.
In growth modeling an outcome measured at four time points can be represented in a data set in two ways. In the wide format, the outcome is represented as four variables on a single record. In the long format, the outcome is represented as a single variable using four records, one for each time point. The DATA WIDETOLONG command is used to rearrange data from a multivariate wide format to a univariate long format.
When the data are rearranged, the set of outcomes is given a new variable name and ID and repetition variables are created. These new variable names must be placed on the USEVARIABLES statement of the VARIABLE command if they are used in the analysis. They must be placed after any original variables. If the ID variable is used as a cluster variable, this must be specified using the CLUSTER option of the VARIABLE command.
The creation of the new variables in the DATA WIDETOLONG command occurs after any transformations in the DEFINE command and any of the other DATA transformation commands. If listwise deletion is used, it occurs after the data have been rearranged. Following is a description of the options used in the DATA WIDETOLONG command.
The WIDE option is used to identify sets of variables in the wide format data set that will be converted into single variables in the long format data set. These variables must be variables from the NAMES statement of the VARIABLE command. The WIDE option is specified as follows:
WIDE = y1-y4 | x1-x4;
where y1, y2, y3, and y4 represent one variable measured at four time points and x1, x2, x3, and x4 represent another variable measured at four time points.
The LONG option is used to provide names for the new variables in the long format data set. There should be the same number of names as there are sets of variables in the WIDE statement. The LONG option is specified as follows:
LONG = y | x;
where y is the name assigned to the set of variables y1-y4 on the WIDE statement and x is the name assigned to the set of variables x1-x4.
The IDVARIABLE option is used to provide a name for the variable that provides information about the unit to which the record belongs. In univariate growth modeling, this is the person identifier which is used as a cluster variable. The IDVARIABLE option is specified as follows:
IDVARIABLE = subject;
where subject is the name of the variable that contains information about the unit to which the record belongs. If an id variable is specified using the IDVARIABLE option of the VARIABLE command, the values of this variable are used for the variable specified using the IDVARIABLE option. This option is not required.
The REPETITION option is used to provide a name for the variable that contains information on the order in which the variables were measured. The REPETITION option is specified as follows:
REPETITION = time;
where time is the variable that contains information on the order in which the variables were measured. This variable assigns consecutive values starting with zero to the repetitions. This variable can be used in a growth model as a time score variable. This option is not required.
In growth modeling an outcome measured at four time points can be represented in a data set in two ways. In the long format, the outcome is represented as a single variable using four records, one for each time point. In the wide format, the outcome is represented as four variables on a single record. The DATA LONGTOWIDE command is used to rearrange data from a univariate long format to a multivariate wide format.
When the data are rearranged, the outcome is given a set of new variable names. These new variable names must be placed on the USEVARIABLES statement of the VARIABLE command if they are used in the analysis. They must be placed after any original variables.
The creation of the new variables in the DATA LONGTOWIDE command occurs after any transformations in the DEFINE command and any of the other DATA transformation commands. Following is a description of the options used in the DATA LONGTOWIDE command.
LONG
The LONG option is used to identify the variables in the long format data set that will be used to create sets of variables in the wide format data set. These variables must be variables from the NAMES statement of the VARIABLE command. The LONG option is specified as follows:
LONG = y | x;
where y and x are two variables that have been measured at multiple time points which are represented by multiple records.
The WIDE option is used to provide sets of names for the new variables in the wide format data set. There should be the same number of sets of names as there are variables in the LONG statement. The number of names in each set corresponds to the number of time points at which the variables in the long data set were measured. The WIDE option is specified as follows:
WIDE = y1-y4 | x1-x4;
where y1, y2, y3, and y4 are the names for the variable y in the wide data set and x1, x2, x3, and x4 are the names for the variable x in the wide data set.
The IDVARIABLE option is used to identify the variable in the long data set that contains information about the unit to which each record belongs. The IDVARIABLE option is specified as follows:
IDVARIABLE = subject;
where subject is the name of the variable that contains information about the unit to which each record belongs. This variable becomes the identifier for each observation in the wide data set. The IDVARIABLE option of the VARIABLE command cannot be used to select a different identifier.
The REPETITION option is used to identify the variable that contains information about the times at which the variables in the long data set were measured. The REPETITION option is specified as follows:
REPETITION = time;
where time is the variable that contains information about the time at which the variables in the long data set were measured. If the time variable does not contain consecutive integer values starting at zero, the time values must be given. For example,
REPETITION = time (4 8 16);
specifies that the values 4, 8, and 16 are the values of the variable time. The number of values should be equal to the number of variables in the WIDE option and the order of the values should correspond to the order of the variables.
The DATA TWOPART command is used to create a binary and a continuous variable from a continuous variable with a floor effect for use in two-part (semicontinuous) modeling (Duan et al., 1983; Olsen & Schafer, 2001). One situation where this occurs is when variables have a preponderance of zeros.
A set of binary and continuous variables are created using the value specified in the CUTPOINT option of the DATA TWOPART command or zero which is the default. The two variables are created using the following rules:
1. If the value of the original variable is missing, both the new binary and the new continuous variable values are missing.
2. If the value of the original variable is greater than the cutpoint value, the new binary variable value is one and the new continuous variable value is the log of the original variable as the default.
3. If the value of the original variable is less than or equal to the cutpoint value, the new binary variable value is zero and the new continuous variable value is missing.
The new variables must be placed on the USEVARIABLES statement of the VARIABLE command if they are used in the analysis. These variables must come after any original variables. If the binary variables are used as dependent variables in the analysis, they must be declared as categorical using the CATEGORICAL option of the VARIABLE command.
The creation of the new variables in the DATA TWOPART command occurs after any transformations in the DEFINE command and before any transformations using the DATA MISSING command. Following is a description of the options used in the DATA TWOPART command.
The NAMES option identifies the variables that are used to create a set of binary and continuous variables. These variables must be variables from the NAMES statement of the VARIABLE command. The NAMES option is specified as follows:
NAMES = smoke1-smoke4;
where smoke1, smoke2, smoke3, and smoke4 are the semicontinuous variables that are used to create a set of binary and continuous variables.
The CUTPOINT option is used to provide the value that is used to divide the original variables into a set of binary and continuous variables. The default value for the CUTPOINT option is zero. The CUTPOINT option is specified as follows:
CUTPOINT = 1;
where variables are created based on values being less than or equal to one or greater than one.
The BINARY option is used to assign names to the new set of binary variables. The BINARY option is specified as follows:
BINARY = u1-u4;
where u1, u2, u3, and u4 are the names of the new set of binary variables.
The CONTINUOUS option is used to assign names to the new set of continuous variables. The CONTINUOUS option is specified as follows:
CONTINUOUS = y1-y4;
where y1, y2, y3, and y4 are the names of the new set of continuous variables.
The TRANSFORM option is used to transform the new continuous variables. The LOG function is the default. The following functions can be used with the TRANSFORM option:
LOG base e log LOG (y);
LOG10 base 10 log LOG10 (y);
EXP exponential EXP (y);
SQRT square root SQRT (y);
ABS absolute value ABS(y);
SIN sine SIN (y);
COS cosine COS (y);
TAN tangent TAN(y);
ASIN arcsine ASIN (y);
ACOS arccosine ACOS (y);
ATAN arctangent ATAN (y);
NONE no transformation
The TRANSFORM option is specified as follows:
TRANSFORM = NONE;
where specifying NONE results in no transformation of the new continuous variables.
The DATA MISSING command is used to create a set of binary variables that are indicators of missing data or dropout for another set of variables. Dropout indicators can be scored as discrete-time survival indicators or dropout dummy indicators. The new variables can be used to study non-ignorable missing data (Little & Rubin, 2002; Muthén et al., 2011).
The new variables must be placed on the USEVARIABLES statement of the VARIABLE command if they are used in the analysis. These variables must come after any original variables. If the binary variables are used as dependent variables in the analysis, they must be declared as categorical using the CATEGORICAL option of the VARIABLE command.
The creation of the new variables in the DATA MISSING command occurs after any transformations in the DEFINE command and after any transformations using the DATA TWOPART command. Following is a description of the options used in the DATA MISSING command.
The NAMES option identifies the set of variables that are used to create a set of binary variables that are indicators of missing data. These variables must be variables from the NAMES statement of the VARIABLE command. The NAMES option is specified as follows:
NAMES = drink1-drink4;
where drink1, drink2, drink3, and drink4 are the set of variables for which a set of binary indicators of missing data are created.
The BINARY option is used to assign names to the new set of binary variables. The BINARY option is specified as follows:
BINARY = u1-u4;
where u1, u2, u3, and u4 are the names of the new set of binary variables.
For TYPE=MISSING, the number of binary indicators is equal to the number of variables in the NAMES statement. For TYPE=SDROPOUT and TYPE=DDROPOUT, the number of binary indicators is one less than the number of variables in the NAMES statement because dropout cannot occur before the second time point an individual is observed.
The TYPE option is used to specify how missingness is coded. It has three settings: MISSING, SDROPOUT, and DDROPOUT. The default is MISSING. For the MISSING setting, a binary missing data indicator variable is created. For the SDROPOUT setting, which is used with selection missing data modeling, a binary discrete-time (event-history) survival dropout indicator is created. For the DDROPOUT setting, which is used with pattern-mixture missing data modeling, a binary dummy dropout indicator is created. The TYPE option is specified as follows:
TYPE = SDROPOUT;
Following are the rules for creating the set of binary variables for the MISSING setting:
1. If the value of the original variable is missing, the new binary variable value is one.
2. If the value of the original variable is not missing, the new binary variable value is zero.
For the SDROPOUT and DDROPOUT settings, the set of indicator variables is defined by the last time point an individual is observed.
Following are the rules for creating the set of binary variables for the SDROPOUT setting:
1. The value one is assigned to the time point after the last time point an individual is observed.
2. The value missing is assigned to all time points after the value of one.
3. The value zero is assigned to all time points before the value of one.
Following are the rules for creating the set of binary variables for the DDROPOUT setting:
1. The value one is assigned to the time point after the last time point an individual is observed.
2. The value zero is assigned to all other time points.
The DESCRIPTIVE option is used in conjunction with TYPE=BASIC of the ANALYSIS command and the SDROPOUT and DDROPOUT settings of the TYPE option to specify the sets of variables for which additional descriptive statistics are computed. For each variable, the mean and standard deviation are computed using all observations without missing on the variable. Means and standard deviations are provided for the following sets of observations whose definitions are based on missing data patterns:
Dropouts after each time point – Individuals who drop out before the next time point and do not return to the study
Non-dropouts after each time point – Individuals who do not drop out before the next time point
Total Dropouts – Individuals who are missing at the last time point
Dropouts no intermittent missing – Individuals who do not return to
the study once they have dropped out
Dropouts intermittent missing – Individuals who drop out and return
to the study
Total Non-dropouts – Individuals who are present at the last time point
Non-dropouts complete data – Individuals with complete data
Non-dropouts intermittent missing – Individuals who have missing
data but are present at the last time point
Total sample
The first set of variables given in the DESCRIPTIVE statement is the outcome variable. This set of variables defines the number of time points in the model. If the other sets of variables do not have the same number of time points, the asterisk (*) is used as a placeholder. Sets of variables are separated by the | symbol. Following is an example of how to specify the DESCRIPTIVE option:
DESCRIPTIVE = y0-y5 | x0-x5 | * z1-z5;
The first set of variables, y0-y5 defines the number of time points as six. The last set of variables has only five measures. An asterisk (*) is used as a placeholder for the first time point.
The DATA SURVIVAL command is used to create variables for discrete-time survival modeling where a binary discrete-time survival (event-history) variable represents whether or not a single non-repeatable event has occurred in a specific time period.
A set of binary discrete-time survival variables is created using the following rules:
1. If the value of the original variable is missing, the new binary variable value is missing.
2. If the value of the original variable is greater than the cutpoint value, the new binary variable value is one which represents that the event has occurred.
3. If the value of the original variable is less than or equal to the cutpoint value, the new binary variable value is zero which represents that the event has not occurred.
4. After a discrete-time survival variable for an observation is assigned the value one, subsequent discrete-time survival variables for that observation are assigned the value of the missing value flag.
The new variables must be placed on the USEVARIABLES statement of the VARIABLE command if they are used in the analysis. These variables must come after any original variables. If the binary variables are used as dependent variables in the analysis, they must be declared as categorical using the CATEGORICAL option of the VARIABLE command.
The creation of the new variables in the DATA SURVIVAL command occurs after any transformations in the DEFINE command, the DATA TWOPART command, and the DATA MISSING command. Following is a description of the options used in the DATA SURVIVAL command.
The NAMES option identifies the variables that are used to create a set of binary event-history variables. These variables must be variables from the NAMES statement of the VARIABLE command. The NAMES option is specified as follows:
NAMES = dropout1-dropout4;
where dropout1, dropout2, dropout3, and dropout4 are the variables that are used to create a set of binary event-history variables.
The CUTPOINT option is used provide the value to use to create a set of binary event-history variables from a set of original variables. The default value for the CUTPOINT option is zero. The CUTPOINT option is specified as follows:
CUTPOINT = 1;
where variables are created based on values being less than or equal to one or greater than one.
The BINARY option is used to assign names to the new set of binary event-history variables. The BINARY option is specified as follows:
BINARY = u1-u4;
where u1, u2, u3, and u4 are the names of the new set of binary event-history variables.
The DATA COHORT command is used to rearrange longitudinal data from a format where time points represent measurement occasions to a format where time points represent age or another time-related variable. It is available only for continuous outcomes. Multiple cohort analysis is described in Chapter 14.
The new variables must be placed on the USEVARIABLES statement of the VARIABLE command if they are used in the analysis.
These variables must come after any original variables. The creation of the new variables in the DATA COHORT command occurs after any transformations in the DEFINE command. Following is a description of the options used in the DATA COHORT command.
The COHORT option is used when data have been collected using a multiple cohort design. The COHORT option is used in conjunction with the TIMEMEASURES and TNAMES options that are described below. Variables used with the COHORT option must be variables from the NAMES statement of the VARIABLE command. Following is an example of how the COHORT option is specified:
COHORT IS birthyear (63 64 65);
where birthyear is a variable in the data set to be analyzed, and the numbers in parentheses following the variable name are the values that the birthyear variable contains. Birth years of 1963, 1964, and 1965 are included in the example below. The cohort variable must contain only integer values.
COPATTERN
The COPATTERN option is used when data are both missing by design and have been collected using a multiple cohort design. Variables used with the COPATTERN option must be variables from the NAMES statement of the VARIABLE command. Following is an example of how the COPATTERN option is specified:
COPATTERN = cohort (67=y1 y2 y3 68=y4 y5 y6 69=y2 y3 y4);
where cohort is a variable that provides information about both the cohorts included in the data set and the patterns of variables for each cohort. In the example above, individuals in cohort 67 should have information on y1, y2, and y3; individuals in cohort 68 should have information on y4, y5, and y6; and individuals in cohort 69 should have information on y2, y3, and y4. Individuals who have missing values on any variable for which they are expected to have information are eliminated from the analysis. The copattern variable must contain only integer values.
The COHRECODE option is used in conjunction with either the COHORT or COPATTERN options to recode the values of the cohort or copattern variable. The COHRECODE option is specified as follows:
COHRECODE = (1=67 2=68 3=69 4=70);
where the original values of 1, 2, 3, and 4 of the cohort or copattern variable are recoded to 67, 68, 69, and 70, respectively. If the COHRECODE option is used, all values of the original variable must be recoded to be included in the analysis. Observations with values that are not recoded will be eliminated from the analysis.
The TIMEMEASURES option is used with multiple cohort data to specify the years in which variables to be used in the analysis were measured. It is used in conjunction with the COHORT and COPATTERN options to determine the ages that are represented in the multiple cohort data set. Variables used with the TIMEMEASURES option must be variables from the NAMES statement of the VARIABLE command. Following is an example of how the TIMEMEASURES option is specified:
TIMEMEASURES = y1 (82) y2 (84) y3 (85) y4 (88) y5 (94);
where y1, y2, y3, y4, and y5 are original variables that are to be used in the analysis, and the numbers in parentheses following each of these variables represent the years in which they were measured. In this situation, y1, y2, y3, y4, and y5 are the same measure, for example, frequency of heavy drinking measured on multiple occasions.
The TIMEMEASURES option can be used to identify more than one measure that has been measured repeatedly as shown in the following example:
TIMEMEASURES = y1 (82) y2 (84) y3 (85) y4 (88) y5 (94) |
y6 (82) y7 (85) y8 (90) y9 (95) |
x1 (83) x2(88) x3 (95);
where each set of variables separated by the symbol | represents repeated measures of that variable. For example, y1, y2, y3, y4, and y5 may represent repeated measures of heavy drinking; y6, y7, y8, and y9 may represent repeated measures of alcohol dependence; and x1, x2, and x3 may represent repeated measures of marital status.
The TNAMES option is used to generate variable names for the new multiple cohort analysis variables. A root name is specified for each set of variables mentioned using the TIMEMEASURES option. The age of the respondent at the time the variable was measured is attached to the root name. The age is determined by subtracting the cohort value from the year the variable was measured. Following is an example of how the TNAMES option is specified:
TNAMES = hd;
where hd is the root name for the new variables.
Following is an example of how the TNAMES option is specified for the TIMEMEASURES and COHORT options when multiple outcomes are measured:
TNAMES = hd | dep | marstat;
Following are the variables that would be created:
hd22, hd24, hd25, hd26, hd27, hd28, hd29, hd30,
hd31, hd32, hd33, hd34, hd36, hd37, hd38, hd39,
dep22, dep24, dep25, dep26, dep27, dep28, dep29, dep30,
dep32, dep33, dep35, dep36, dep37, dep38, dep39, dep40,
marstat23, marstat25, marstat26, marstat27, marstat28
marstat30, marstat31, marstat32, marstat33, marstat35
marstat37, marstat38, marstat39, marstat40.
There is no hd variable for ages 23 and 35, no dep variable for ages 23, 31, and 34, and no marstat variable for ages 24, 29, 34, and 36 because these ages are not represented by the combination of cohort values and years of measurement.
The VARIABLE command is used to provide information about the variables in the data set to be analyzed. The VARIABLE command has options for naming and describing the variables in the data set to be analyzed, subsetting the data set on observations, subsetting the data set on variables, and specifying missing values for each variable.
Following are the options for the VARIABLE command:
|
VARIABLE: |
|
|
|
|
|
|
|
NAMES ARE |
names of variables in the data set; |
|
|
USEOBSERVATIONS ARE |
conditional statement to select observations; |
all observations in data set |
|
USEVARIABLES ARE |
names of analysis variables; |
all variables in NAMES |
|
MISSING ARE |
variable (#); |
|
|
|
. ; |
|
|
|
* ; |
|
|
|
BLANK; |
|
|
CENSORED ARE |
names, censoring type, and inflation status for censored dependent variables; |
|
|
CATEGORICAL ARE |
names of binary and ordered categorical (ordinal) dependent variables (model); |
|
|
NOMINAL ARE |
names of unordered categorical (nominal) dependent variables; |
|
|
COUNT ARE |
names of count variables (model); |
|
|
DSURVIVAL ARE |
names of discrete-time survival variables; |
|
|
GROUPING IS |
name of grouping variable (labels); |
|
|
IDVARIABLE IS |
name of ID variable; _RECNUM; |
|
|
FREQWEIGHT IS |
name of frequency (case) weight variable; |
|
|
TSCORES ARE |
names of observed variables with information on individually-varying times of observation; |
|
|
AUXILIARY = |
names of auxiliary variables; names of auxiliary variables (M); names of auxiliary variables (R3STEP); names of auxiliary variables (R); names of auxiliary variables (BCH); names of auxiliary variables (DU3STEP); names of auxiliary variables (DCATEGORICAL); names of auxiliary variables (DE3STEP); names of auxiliary variables (DCONTINUOUS); names of auxiliary variables (E); |
|
|
CONSTRAINT = |
names of observed variables that can be used in the MODEL CONSTRAINT command; |
|
|
PATTERN IS |
name of pattern variable (patterns); |
|
|
STRATIFICATION IS |
name of stratification variable; |
|
|
CLUSTER IS |
name of cluster variables; |
|
|
WEIGHT IS |
name of sampling weight variable; |
|
|
WTSCALE IS |
UNSCALED; |
CLUSTER |
|
|
CLUSTER; |
|
|
|
ECLUSTER; |
|
|
BWEIGHT |
name of between-level sampling weight variable; |
|
|
B2WEIGHT IS |
name of the level 2 sampling weight variable; |
|
|
B3WEIGHT IS |
name of the level 3 sampling weight variable; |
|
|
BWTSCALE IS |
UNSCALED; SAMPLE; |
SAMPLE |
|
REPWEIGHTS ARE |
names of replicate weight variables; |
|
|
SUBPOPULATION IS |
conditional statement to select subpopulation; |
all observations in data set |
|
FINITE = |
name of variable; name of variable (FPC); name of variable (SFRACTION); name of variable (POPULATION); |
FPC |
|
CLASSES = |
names of categorical latent variables (number of latent classes); |
|
|
KNOWNCLASS = |
name of categorical latent variable with known class membership (labels); |
|
|
TRAINING = |
names of training variables; names of variables (MEMBERSHIP); names of variables (PROBABILITIES); names of variables (PRIORS); |
MEMBERSHIP |
|
WITHIN ARE WITHIN ARE (label) |
names of individual-level observed variables; names of individual-level observed variables; |
|
|
BETWEEN ARE BETWEEN ARE (label) |
names of cluster-level observed variables; names of cluster-level observed variables; |
|
|
SURVIVAL ARE |
names and time intervals for time-to-event variables; |
|
|
TIMECENSORED ARE
LAGGED ARE TINTERVAL IS |
names and values of variables that contain right censoring information; names of lagged variables (lag); name of time variable (interval); |
(0 = NOT 1 = RIGHT)
|
The VARIABLE command is a required command. The NAMES option is a required option. Default settings are shown in the last column. If the default settings are appropriate for the analysis, nothing needs to be specified except the NAMES option.
Note that commands and options can be shortened to four or more letters. Option settings can be referred to by either the complete word or the part of the word shown above in bold type.
The NAMES option is used to assign names to the variables in the data set named using the FILE option of the DATA command. This option is required. The variable names can be separated by blanks or commas and can be up to 8 characters in length. Variable names must begin with a letter. They can contain only letters, numbers, and the underscore symbol. The program makes no distinction between upper and lower case letters. Following is an example of how the NAMES option is specified:
NAMES ARE gender ethnic income educatn drink_st agedrink;
Variable names are generated if a list of variables is specified using the NAMES option. For example,
NAMES ARE y1-y5 x1-x3;
generates the variable names y1 y2 y3 y4 y5 x1 x2 x3.
NAMES ARE itema-itemd;
generates the variable names itema itemb itemc itemd.
SUBSETTING OBSERVATIONS AND VARIABLES
There are options for selecting a subset of observations or variables from the data set named using the FILE option of the DATA command. The USEOBSERVATIONS option is used to select a subset of observations from the data set. The USEVARIABLES option is used to select a subset of variables from the data set.
The USEOBSERVATIONS option is used to select observations for an analysis from the data set named using the FILE option of the DATA command. This option is not available for summary data. The USEOBSERVATIONS option selects only those observations that satisfy the conditional statement specified after the equal sign. For example, the following statement selects observations with the variable ethnic equal to 1 and the variable gender equal to 2:
USEOBSERVATIONS = ethnic EQ 1 AND gender EQ 2;
Only variables from the NAMES statement of the VARIABLE command can be used in the conditional statement of the USEOBSERVATIONS option. Logical operators, not arithmetic operators, must be used in the conditional statement. Following are the logical operators that can be used in conditional statements to select observations for analysis:
AND logical and
OR logical or
NOT logical not
EQ equal ==
NE not equal /=
GE greater than or equal to >=
LE less than or equal to <=
GT greater than >
LT less than <
As shown above, some of the logical operators can be referred to in two different ways. For example, equal can be referred to as EQ or ==.
The USEVARIABLES option is used to select variables for an analysis. It can be used with individual data or summary data. Variables included on the USEVARIABLES statement can be variables from the NAMES statement of the VARIABLE command and variables created using the DEFINE command and the DATA transformation commands. New variables created using the DEFINE command and the DATA transformation commands must be included on the USEVARIABLES statement.
The USEVARIABLES option identifies the observed dependent and independent variables that are used in an analysis. Variables with special functions such as grouping variables do not need to be included on the USEVARIABLES statement unless they are new variables created using the DEFINE command or the DATA transformation commands. Following is an example of how to specify the USEVARIABLES option:
USEVARIABLES ARE gender income agefirst;
Variables on the USEVARIABLES statement must follow a particular order. The order of the variables is important because it determines the order of variables used with the list function. The set of original variables from the NAMES statement of the VARIABLE command must be listed before the set of new variables created using the DEFINE command or the DATA transformation commands. Within the two sets of original and new variables, any order is allowed.
If all of the original variables plus some of the new variables are used in the analysis, the keyword ALL can be used as the first entry in the USEVARIABLES statement. This indicates that all of the original variables from the NAMES statement of the VARIABLE command are used in the analysis. The keyword ALL is followed by the names of the new variables created using the DEFINE command or the DATA transformation commands that will be used in the analysis. Following is an example of how to specify the USEVARIABLES option for this situation:
USEVARIABLES = ALL hd1 hd2 hd3;
where ALL refers to the total set of original variables and hd1, hd2, and hd3 are new variables created using the DEFINE command or the DATA transformation commands.
The MISSING option is used to identify the values or symbol in the analysis data set that are treated as missing or invalid. Any numeric value and the non-numeric symbols of the period, asterisk (*), or blank can be used as missing value flags. There is no default missing value flag. Numeric and non-numeric missing value flags cannot be combined. The blank cannot be used as a missing value flag for data in free format. When a list of missing value flags contains a negative number, the entries must be separated by commas.
NON-NUMERIC MISSING VALUE FLAGS
The period (.), the asterisk (*), or the blank can be used as non-numeric missing value flags. Only one non-numeric missing value flag can be used for a particular data set. This missing value flag applies to all variables in the data set. The blank cannot be used with free format data. With fixed format data, blanks in the data not declared as missing value flags are treated as zeroes.
The following command indicates that the period is the missing value flag for all variables in the data set:
MISSING ARE . ;
The blank can be a missing value flag only in fixed format data sets. The following command indicates that blanks are to be considered as missing value flags:
MISSING = BLANK;
Any number of numeric values can be specified as missing value flags for the complete data set or for individual variables. The keyword ALL can be used with the MISSING option if all variables have the same numeric value(s) as missing value flags.
The following statement specifies that the number 9 is the missing value flag for all variables in the data set:
MISSING ARE ALL (9);
The following example specifies that for the variable ethnic, the numbers 9 and 99 are missing value flags, while for the variable y1, the number 1 is the missing value flag:
MISSING ARE ethnic (9 99) y1 (1);
The list function can be used with the MISSING option to specify a list of missing value flags and/or a set of variables. The order of variables in the list is determined by the order of variables in the NAMES statement of the VARIABLE command. Values of 9, 99, 100, 101, and 102 can be declared as missing value flags for all variables in a data set by the following specification:
MISSING ARE ALL (9 99-102);
Missing values can be specified for a list of variables as follows:
MISSING ARE gender-income (9 30 98-102);
The statement above specifies that the values of 9, 30, 98, 99, 100, 101, and 102 are missing value flags for the list of variables beginning with gender and ending with income.
If a single missing value flag is negative, it can be specified as described above. If there are several negative missing value flags, they must be separated by commas to distinguish between the list function and a negative value. The following example specifies that for the variable ethnic, the numbers -9 and -99 are missing value flags.
MISSING ARE ethnic (-9, -99);
The list function can be used with negative missing value flags. It is specified as:
MISSING = ALL (-778- -775);
The statement above specifies that the values of -778, -777, -776, and -775 are missing value flags for all variables in the data set.
MEASUREMENT SCALE OF OBSERVED DEPENDENT VARIABLES
All observed dependent variables are assumed to be measured on a continuous scale unless the CENSORED, CATEGORICAL, NOMINAL, and/or COUNT options are used. The specification of the scale of the dependent variables determines how the variables are treated in the model and its estimation. Independent variables can be binary or continuous. The scale of the independent variables has no influence on the model or its estimation. The distinction between dependent and independent variables is described in Chapter 17.
Variables named using the CENSORED, CATEGORICAL, NOMINAL, and/or COUNT options can be variables from the NAMES statement of the VARIABLE command and variables created using the DEFINE command and the DATA transformation commands.
The CENSORED option is used to specify which dependent variables are treated as censored variables in the model and its estimation, whether they are censored from above or below, and whether a censored or censored-inflated model will be estimated.
The CENSORED option is specified as follows for a censored model:
CENSORED ARE y1 (a) y2 (b) y3 (a) y4 (b);
where y1, y2, y3, y4 are censored dependent variables in the analysis. The letter a in parentheses following the variable name indicates that the variable is censored from above. The letter b in parentheses following the variable name indicates that the variable is censored from below. The lower and upper censoring limits are determined from the data.
The CENSORED option is specified as follows for a censored-inflated model:
CENSORED ARE y1 (ai) y2 (bi) y3 (ai) y4 (bi);
where y1, y2, y3, y4 are censored dependent variables in the analysis. The letters ai in parentheses following the variable name indicate that the variable is censored from above and that a censored-inflated model will be estimated. The letters bi in parentheses following the variable name indicate that the variable is censored from below and that a censored-inflated model will be estimated. The lower and upper censoring limits are determined from the data.
With a censored-inflated model, two variables are considered, a censored variable and an inflation variable. The censored variable takes on values for individuals who are able to assume values of the censoring point and beyond. The inflation variable is a binary latent variable for which the value one denotes that an individual is unable to assume any value except the censoring point. The inflation variable is referred to by adding to the name of the censored variable the number sign (#) followed by the number 1. In the example above, the censored variables available for use in the MODEL command are y1, y2, y3, and y4, and the inflation variables available for use in the MODEL command are y1#1, y2#1, y3#1, and y4#1.
The CATEGORICAL option is used to specify which dependent variables are treated as binary or ordered categorical (ordinal) variables in the model and its estimation and the type of model to be estimated. Both probit and logistic regression models can be estimated for categorical variables. For binary variables, the following IRT models can be estimated: two-parameter normal ogive, two-parameter logistic, three-parameter logistic, and four-parameter logistic. For ordered categorical (ordinal) variables, the following IRT models can be estimated: generalized partial credit with logistic and graded-response with probit (normal ogive) and logistic. For a nominal IRT model, use the NOMINAL option.
For categorical dependent variables, there are as many thresholds as there are categories minus one. The thresholds are referred to in the MODEL command by adding to the variable name the dollar sign ($) followed by a number. The threshold for a binary variable u1 is referred to as u1$1. The two thresholds for a three-category variable u2 are referred to as u2$1 and u2$2. Ordered categorical dependent variables cannot have more than 10 categories. The number of categories is determined from the data.
The CATEGORICAL option is specified as follows:
CATEGORICAL ARE u2 u3 u7-u13;
where u2, u3, u7, u8, u9, u10, u11, u12, and u13 are binary or ordered categorical dependent variables in the analysis. With weighted least squares and Bayes estimation, a probit model is estimated. For binary variables, this is a two-parameter normal ogive model. For ordered categorical (ordinal) variables, this is a graded response model. With maximum likelihood estimation, a logistic model is estimated as the default. For binary variables, this is a two-parameter logistic model. For ordered categorical (ordinal) variables, this is a proportional odds model which is the same as a graded response model. Probit models can also be estimated with maximum likelihood estimation using the LINK option of the ANALYSIS command.
The CATEGORICAL option for a generalized partial credit model is specified as follows:
CATEGORICAL = u1 –u3 (gpcm) u10 (gpcm);
where the variables u1, u2, u3, and u10 are ordered categorical (ordinal) variables for which a generalized partial credit model will be estimated. The partial credit model has c-1 step parameters for an item with c categories and one slope parameter (Asparouhov & Muthén, 2016). The step parameters are referred to in the same way as thresholds. The first step parameter for a three-category ordered categorical (ordinal) variable u1 is referred to as u1$1. The second step parameter is referred to as u1$2.
The CATEGORICAL option for a three-parameter logistic model is specified as follows:
CATEGORICAL = u1 –u3 (3pl) u10 (3pl);
where the variables u1, u2, u3, and u10 are binary variables for which a three-parameter logistic model will be estimated. The guessing parameter cannot be referred to directly. Instead a parameter related to the guessing parameter is referred to (Asparouhov & Muthén, 2016). This parameter is referred to as the second threshold. The first threshold for a binary variable u1 is referred to as u1$1. The second threshold is referred to as u1$2.
The CATEGORICAL option for a four-parameter logistic model is specified as follows:
CATEGORICAL = u1 –u3 (4pl) u10 (4pl);
where the variables u1, u2, u3, and u10 are binary variables for which a four-parameter logistic model will be estimated. The lower asymptote (guessing) and upper asymptote parameters cannot be referred to directly. Instead a parameter which is related to the lower asymptote (guessing) and a parameter which is related to the upper asymptote parameter are referred to (Asparouhov & Muthén, 2016). The parameter related to the lower asymptote (guessing) parameter is referred to as the second threshold. The parameter related to the upper asymptote parameter is referred to as the third threshold. The first threshold for a binary variable u1 is referred to as u1$1. The second threshold is referred to as u1$2. The third threshold is referred to as u1$3.
RECODING OF DEPENDENT VARIABLES
The estimation of the model for binary or ordered categorical dependent variables uses zero to denote the lowest category, one to denote the second lowest category, two to denote the third lowest category, etc. If the variables are not coded this way in the data, they are automatically recoded as described below. When data are saved for subsequent analyses, the recoded categories are saved.
Following are examples of situations in which data are recoded by the program:
Categories in Original Data Categories in Recoded Data
1 2 3 4 0 1 2 3
2 3 4 5 0 1 2 3
2 5 8 9 0 1 2 3
0 1 no recode needed
1 2 0 1
In most situations, the default recoding is appropriate. In multiple group analysis and growth modeling, the default recoding may not be appropriate because the categories observed in the data for a variable may not be the same across groups or time. For example, it is sometimes the case that individuals are observed in lower categories at earlier time points and higher categories at later time points. Several variations of the CATEGORICAL option are available for these situations. These are allowed only for maximum likelihood estimation.
Using the automatic recoding, each variable is recoded using the categories found in the data for that variable. Following is an example of how to specify the CATEGORICAL option so that each variable is recoded using the categories found in the data for a set of variables:
CATEGORICAL u1-u3 (*);
where u1, u2, and u3 are a set of ordered categorical variables and the asterisk (*) in parentheses indicates that the categories of each variable are to be recoded using the categories found in the data for the set of variables not for each variable. Based on the original data shown in the table below, where the rows represent observations and the columns represent variables, the set of variables are found to have four possible categories: 1, 2, 3, and 4. The variable u1 has observed categories 1 and 2; u2 has observed categories 1, 2, and 3; and u3 has observed categories 2, 3, and 4. The recoded values are shown in the table below.
|
Categories in the Original Data Set |
Categories in the Recoded Data Set |
||||
|
u1 |
u2 |
u3 |
u1 |
u2 |
u3 |
|
1 |
2 |
3 |
0 |
1 |
2 |
|
1 |
1 |
2 |
0 |
0 |
1 |
|
2 |
2 |
2 |
1 |
1 |
1 |
|
2 |
3 |
4 |
1 |
2 |
3 |
The CATEGORICAL option can be used to give a set of categories that are allowed for a variable or set of variables rather than having these categories determined from the data. Following is an example of how to specify this:
CATEGORICAL = u1-u3 (1-6);
where the set of variables u1, u2, and u3 can have the categories of 1, 2, 3, 4, 5, and 6. In this example, 1 will be recoded as 0, 2 as 1, 3 as 2, 4 as 3, 5 as 4, and 6 as 5.
Another variation of this is:
CATEGORICAL = u1-u3 (2 4 6);
where the set of variables u1, u2, and u3 can have the categories 2, 4, and 6. In this example, 2 will be recoded as 0, 4 as 1, and 6 as 2.
The CATEGORICAL option can be used to specify that different sets of variables have different sets of categories by using the | symbol. For example,
CATEGORICAL = u1-u3 (*) | u4-u6 (2-5) | u7-u9;
specifies that for the variables u1, u2, and u3, the possible categories are taken from the data for the set of variables; for the variables u4, u5, and u6, the possible categories are 2, 3, 4, and 5; and for the variables u7, u8, and u9, the possible categories are the default, that is, the possible categories are taken from the data for each variable.
The NOMINAL option is used to specify which dependent variables are treated as unordered categorical (nominal) variables in the model and its estimation. Unordered categorical dependent variables cannot have more than 10 categories. The number of categories is determined from the data. The NOMINAL option is specified as follows:
NOMINAL ARE u1 u2 u3 u4;
where u1, u2, u3, u4 are unordered categorical dependent variables in the analysis.
For nominal dependent variables, all categories but the last category can be referred to. The last category is the reference category. The categories are referred to in the MODEL command by adding to the variable name the number sign (#) followed by a number. The three categories of a four-category nominal variable are referred to as u1#1, u1#2, and u1#3.
The estimation of the model for unordered categorical dependent variables uses zero to denote the lowest category, one to denote the second lowest category, two to denote the third lowest category, etc. If the variables are not coded this way in the data, they are automatically recoded as described below. When data are saved for subsequent analyses, the recoded categories are saved.
Following are examples of situations in which data are recoded by the program:
Categories in Original Data Categories in Recoded Data
1 2 3 4 0 1 2 3
2 3 4 5 0 1 2 3
2 5 8 9 0 1 2 3
0 1 no recode needed
1 2 0 1
The COUNT option is used to specify which dependent variables are treated as count variables in the model and its estimation and the type of model to be estimated. The following models can be estimated for count variables: Poisson, zero-inflated Poisson, negative binomial, zero-inflated negative binomial, zero-truncated negative binomial, and negative binomial hurdle (Long, 1997; Hilbe, 2011). The negative binomial models use the NB-2 variance representation (Hilbe, 2011, p. 63). Count variables may not have negative or non-integer values.
The COUNT option can be specified in two ways for a Poisson model:
COUNT = u1 u2 u3 u4;
or
COUNT = u1 (p) u2 (p) u3 (p) u4 (p);
or using the list function:
COUNT = u1-u4 (p);
The COUNT option can be specified in two ways for a zero-inflated Poisson model:
COUNT = u1-u4 (i);
or
COUNT = u1-u4 (pi);
where u1, u2, u3, and u4 are count dependent variables in the analysis. The letter i or pi in parentheses following the variable name indicates that a zero-inflated Poisson model will be estimated.
With a zero-inflated Poisson model, two variables are considered, a count variable and an inflation variable. The count variable takes on values for individuals who are able to assume values of zero and above following the Poisson model. The inflation variable is a binary latent variable with one denoting that an individual is unable to assume any value except zero. The inflation variable is referred to by adding to the name of the count variable the number sign (#) followed by the number 1. If the inflation parameter value is estimated at a large negative value corresponding to a probability of zero, the inflation part of the model is not needed.
Following is the specification of the COUNT option for a negative binomial model:
COUNT = u1 (nb) u2 (nb) u3 (nb) u4 (nb);
or using the list function:
COUNT = u1-u4 (nb);
With a negative binomial model, a dispersion parameter is estimated. The dispersion parameter is referred to by using the name of the count variable. If the dispersion parameter is estimated at zero, the model is a Poisson model.
Following is the specification of the COUNT option for a zero-inflated negative binomial model:
COUNT = u1- u4 (nbi);
With a zero-inflated negative binomial model, two variables are considered, a count variable and an inflation variable. The count variable takes on values for individuals who are able to assume values of zero and above following the negative binomial model. The inflation variable is a binary latent variable with one denoting that an individual is unable to assume any value except zero. The inflation variable is referred to by adding to the name of the count variable the number sign (#) followed by the number 1. If the inflation parameter value is estimated at a large negative value corresponding to a probability of zero, the inflation part of the model is not needed.
Following is the specification of the COUNT option for a zero-truncated negative binomial model:
COUNT = u1-u4 (nbt);
Count variables for the zero-truncated negative binomial model must have values greater than zero.
Following is the specification of the COUNT option for a negative binomial hurdle model:
COUNT = u1-u4 (nbh);
With a negative binomial hurdle model, two variables are considered, a count variable and a hurdle variable. The count variable takes on values for individuals who are able to assume values of one and above following the truncated negative binomial model. The hurdle variable is a binary latent variable with one denoting that an individual is unable to assume any value except zero. The hurdle variable is referred to by adding to the name of the count variable the number sign (#) followed by the number 1.
The DSURVIVAL option is used in conjunction with the PLOT command to identify the discrete-time survival variables so that survival curves are generated. The DSURVIVAL option is specified as follows:
DSURVIVAL = u1-u4;
where u1 to u4 are discrete-time survival variables.
VARIABLES WITH SPECIAL FUNCTIONS
There are several options that are used to identify variables that have special functions. These variables can be variables from the NAMES statement of the VARIABLE command and variables created using the DEFINE command and the DATA transformation commands. Following is a description of these options and their specifications.
The GROUPING option is used to identify the variable in the data set that contains information on group membership when the data for all groups are stored in a single data set. Multiple group analysis is discussed in Chapter 14. A grouping variable must contain only integer values. Only one grouping variable can be used. If the groups to be analyzed are a combination of more than one variable, a single grouping variable can be created using the DEFINE command. Following is an example of how to specify the GROUPING option:
GROUPING IS gender (1=male 2 = female);
The information in parentheses after the grouping variable name assigns labels to the values of the grouping variable found in the data set. In the example above, observations with gender equal to 1 are assigned the label male, and individuals with gender equal to 2 are assigned the label female. These labels are used in conjunction with the MODEL command to specify model statements specific to each group. Observations that have a value on the grouping variable that is not specified using the GROUPING option are not included in the analysis.
In situations where there are many groups, a shorthand notation can be used for the GROUPING option. It is specified as follows:
GROUPING = country (101-200 225 350-360);
where country is the grouping variable and 101 through 200, 225, and 350 through 360 are the values of country that will be used as groups. The values of the variable country are used as labels in group-specific MODEL commands.
The GROUPING option can be specified by mentioning only the number of groups, for example,
GROUPING = country (34);
where country is the grouping variable and the number 34 specifies that there are 34 groups. The group values are taken from the data. The reference group is the group with the lowest value. Default group labels are used. G1 is the label for the group with the lowest value, g2 is the label for the group with the next value, etc..
The IDVARIABLE option is used in conjunction with the SAVEDATA command to provide an identifier for each observation in the data set that is saved. This is useful for merging the data with another data set. The IDVARIABLE option is specified as follows:
IDVARIABLE = id;
where id is a variable that contains a unique numerical identifier for each observation. The length of this variable may not exceed 16.
If a data set does not contain an identifier variable, the _RECNUM setting can be used as follows to create one:
IDVARIABLE = _RECNUM;
The unique numerical identifier corresponds to the record number of the data set specified using the FILE option of the DATA command.
The FREQWEIGHT option is used to identify the variable that contains frequency (case) weight information. Frequency weights are used when a single record in the data set represents the responses of more than one individual. Frequency weight values must be integers. Frequency weights do not have to sum to the total number of observations in the analysis data set and are not rescaled in any way. Frequency weights are available for all analysis types except TYPE=COMPLEX, TYPE=TWOLEVEL, TYPE=THREELEVEL, TYPE=CROSSCLASSIFIED, and TYPE=EFA. With TYPE=RANDOM, frequency weights are available only with ALGORITHM=INTEGRATION. Following is an example of how the FREQWEIGHT option is specified:
FREQWEIGHT IS casewgt;
where casewgt is the variable that contains frequency weight information.
The TSCORES option is used in conjunction with TYPE=RANDOM to identify the variables in the data set that contain information about individually-varying times of observation for the outcome in a growth model. Variables listed in the TSCORES statement can be used only in AT statements in the MODEL command to define a growth model. For TYPE=TWOLEVEL, ALGORITHM=INTEGRATION must be specified in the ANALYSIS command for this type of analysis. The TSCORES option is specified as follows:
TSCORES ARE a1 a2 a3 a4;
where a1, a2, a3, and a4 are observed variables in the analysis data set that contain the individually-varying times of observation for an outcome at four time points.
Auxiliary variables are variables that are not part of the analysis model. The AUXILIARY option has three uses. One is to identify a set of variables that is not used in the analysis but is saved for use in a subsequent analysis. A second is to identify a set of variables that will be used as missing data correlates in addition to the analysis variables. The third is to automatically carry out the 3-step approach of TYPE=MIXTURE.
SAVED
In the first use of the AUXILIARY option, variables listed on the AUXILIARY statement are saved along with the analysis variables if the SAVEDATA command is used. These variables can be used in graphical displays if the PLOT command is used. If these variables are created using the DEFINE command or the DATA transformation commands, they must be listed on the USEVARIABLES statement of the VARIABLE command in addition to being listed on the AUXILIARY statement. The AUXILIARY option is specified as follows:
AUXILIARY = gender race educ;
where gender, race, and educ are variables that are not used in the analysis but that are saved in conjunction with the SAVEDATA and/or the PLOT commands.
MISSING DATA CORRELATES
In the second use of the AUXILIARY option, it is used in conjunction with TYPE=GENERAL with continuous dependent variables and maximum likelihood estimation to identify a set of variables that will be used as missing data correlates in addition to the analysis variables (Collins, Schafer, & Kam, 2001; Graham, 2003; Asparouhov & Muthén, 2008b; Enders, 2010). This use is not available with MODINDICES, BOOTSTRAP, and models with a set of exploratory factor analysis (EFA) factors in the MODEL command. The setting M in parentheses is placed behind the variables on the AUXILIARY statement that will be used as missing data correlates. Following is an example of how to specify the M setting:
AUXILIARY = z1-z4 (M);
where z1, z2, z3, and z4 are variables that will be used as missing data correlates in addition to the analysis variables.
An alternative specification that is convenient when there are several variables that cannot be specified using the list function is:
AUXILIARY = (M) x1 x3 x5 x7 x9;
where all variables after (M) will be used as missing data correlates in addition to the analysis variables.
3-STEP APPROACH
In the third use of the AUXILIARY option, the 3-step approach using TYPE=MIXTURE is automatically carried out. There are eight settings of the AUXILIARY option that automatically carry out the 3-step approach. Two of these settings are used to identify a set of variables not used in the first step of the analysis that are possible covariates in a multinomial logistic regression for a categorical latent variable. The multimonial logistic regression uses all covariates at the same time. Six of the settings are used to identify a set of variables not used in the first step of the analysis for which the equality of means across latent classes will be tested. The equality of means is tested one variable at a time. Only one of these eight settings can be used in an analysis at a time. Only one categorical latent variable is allowed with the 3-step approach. The manual 3-step approach in described in Asparouhov and Muthen (2014a, b).
The two settings that are used to identify a set of variables not used in the first step of the analysis that are possible covariates in a multinomial logistic regression for a categorical latent variable are R3STEP (Vermunt, 2010; Asparouhov & Muthén, 2012b) and R (Wang et al., 2005). R3STEP is preferred. R is superseded by R3STEP and should be used only for methods research.
The six settings that are used to identify a set of variables not used in the first step of the analysis for which the equality of means across latent classes will be tested are BCH (Bakk & Vermunt, 2015), DU3STEP (Asparouhov & Muthén, 2012b), DCATEGORICAL (Lanza et al., 2013), DE3STEP (Asparouhov & Muthén, 2012b), DCONTINUOUS (Lanza et al., 2013), and E (Asparouhov, 2007). BCH is preferred for continuous distal outcomes. DU3STEP should be used only when there are no class changes between the first and last steps. DCATEGORICAL is for categorical distal outcomes. The following settings for continuous distal outcomes, DE3STEP, DCONTINUOUS, and E, should be used only for methods research.
All of the settings are specified in the same way. The setting in parentheses is placed behind the variables on the AUXILIARY statement that will be used as covariates in the multinomial logistic regression or for which the equality of means will be tested. Following is an example of how to specify the R3STEP setting:
AUXILIARY = race (R3STEP) ses (R3STEP) x1-x5 (R3STEP);
where race, ses, x1, x2, x3, x4, and x5 will be used as covariates in a multinomial logistic regression in a mixture model.
An alternative specification for the eight settings that is convenient when there are several variables that cannot be specified using the list function is:
AUXILIARY = (R3STEP) x1 x3 x5 x7 x9;
where all variables after R3STEP) will be used as covariates in a multinomial logistic regression in a mixture model.
Following is an example of how to specify more than one setting in the same AUXILIARY statement:
AUXILIARY = gender age (BCH) educ ses (BCH) x1-x5 (BCH);
where all of the variables on the AUXILIARY statement will be saved if the SAVEDATA command is used, will be available for plots if the PLOT command is used, and tests of equality of means across latent classes will be carried out for the variables age, ses, x1, x2, x3, x4, and x5.
The CONSTRAINT option is used to identify the variables that can be used in the MODEL CONSTRAINT command. These can be not only variables used in the MODEL command but also other variables. All variables on the CONSTRAINT list are treated as continuous variables in the analysis. Only variables used by the following options cannot be included: GROUPING, PATTERN, COHORT, COPATTERN, CLUSTER, STRATIFICATION, and AUXILIARY. Variables that are part of these options can be used in DEFINE to create new variables that can be used in the CONSTRAINT statement. The CONSTRAINT option is not available for TYPE=RANDOM, TYPE=TWOLEVEL, TYPE=THREELEVEL, TYPE=CROSSCLASSIFIED, TYPE=COMPLEX, and for estimators other than ML, MLR, and MLF. The CONSTRAINT option is specified as follows:
CONSTRAINT = y1 u1;
where y1 and u1 are variables that can be used in the MODEL CONSTRAINT command.
The PATTERN option is used when data are missing by design. The typical use is in situations when, because of the design of the study, all variables are not measured on all individuals in the analysis. This can occur, for example, when individuals receive different forms of a measurement instrument that contain different sets of items. Following is an example of how the PATTERN option is specified:
PATTERN IS design (1= y1 y3 y5 2= y2 y3 y4 3= y1 y4 y5);
where design is a variable in the data set that has integer values of 1, 2, and 3. The variable names listed after each number and the equal sign are variables used in the analysis which should have no missing values for observations with that value on the pattern variable. For example, observations with the value of one on the variable design should have information for variables y1, y3, and y5 and have missing values for y2 and y4. Observations with the value of three on the variable design should have information for variables y1, y4, and y5 and have missing values for variables y2 and y3. The pattern variable must contain only integer values. Observations that have a value for the pattern variable that is not specified using the PATTERN option are not included in the analysis.
There are several options that are used for complex survey data. These include options for stratification, clustering, unequal probabilities of selection (sampling weights), and subpopulation analysis. The variables used with these options can be variables from the NAMES statement of the VARIABLE command and variables created using the DEFINE command and the DATA transformation commands. The exception is that variables used with the SUBPOPULATION option must be variables from the NAMES statement of the VARIABLE command. Following is a description of these options and their specifications.
The STRATIFICATION option is used with TYPE=COMPLEX to identify the variable in the data set that contains information about the subpopulations from which independent probability samples are drawn. Following is an example of how the STRATIFICATION option is used:
STRATIFICATION IS region;
where region is the variable that contains stratification information.
The CLUSTER option is used with TYPE=TWOLEVEL, TYPE=THREELEVEL, TYPE=CROSSCLASSIFIED, and TYPE=COMPLEX to identify the variables in the data set that contain clustering information. One cluster variable is used for TYPE=TWOLEVEL and TYPE=COMPLEX. Two cluster variables are used for TYPE=THREELEVEL, TYPE=CROSSCLASSIFIED, and TYPE=COMPLEX TWOLEVEL. Three cluster variables are used for TYPE=COMPLEX THREELEVEL.
Following is an example of how the CLUSTER option is used with TYPE=TWOLEVEL and TYPE=COMPLEX:
CLUSTER IS school;
where school is the variable that contains clustering information.
Following is an example of how the CLUSTER option is used with TYPE=THREELEVEL:
CLUSTER IS school class;
where school and class are the variables that contain clustering information. The cluster variable for the highest level must come first, that is, classrooms are nested in schools.
Following is an example of how the CLUSTER option is used with TYPE=CROSSCLASSIFIED:
CLUSTER = neighbor school;
where neighbor and school are the variables that contain clustering information. Students are nested in schools crossed with neighborhoods.
Following is an example of how the CLUSTER option is used with TYPE=CROSSCLASSIFIED and time series analysis:
CLUSTER = subject time;
where subject and time are the variables that contain clustering information. In cross-classified time series analysis, subject and time are crossed. There is no nesting because each subject is observed only once at any one time. The cluster variable for subject must precede the cluster variable for time. Within each cluster, data must be ordered by time.
TYPE=COMPLEX TWOLEVEL can be used with either two cluster variables, one stratification and two cluster variables, or one stratification and one cluster variable. Following is an example of using two cluster variables:
CLUSTER = school class;
where school and class are the variables that contain clustering information. The clusters for TYPE=TWOLEVEL are classroom. The standard error and chi-square computations for TYPE=COMPLEX are based on school.
Following is an example with stratification and clustering:
STRATIFICATION = region;
CLUSTER = school;
where the clusters for TYPE=TWOLEVEL are schools and the standard error and chi-square computations for TYPE=COMPLEX are based on region.
TYPE=COMPLEX THREELEVEL can be used with either three cluster variables, one stratification and three cluster variables, or one stratification and two cluster variables. Following is an example of how the CLUSTER option is used with TYPE=COMPLEX THREELEVEL:
CLUSTER IS psu school class;
where psu, school, and class are the variables that contain clustering information. The cluster variable for the highest level must come first, that is, classrooms are nested in schools and schools are nested in psu’s. The clusters for TYPE=THREELEVEL are classroom and school. The standard error and chi-square computations for TYPE=COMPLEX are based on psu’s.
The WEIGHT option is used to identify the variable that contains sampling weight information for non-clustered data using TYPE=GENERAL, clustered data using TYPE=COMPLEX, and level 1 data using TYPE=TWOLEVEL and TYPE=THREELEVEL. Sampling weights are not available for TYPE=CROSSCLASSIFIED. Sampling weights are used when data have been collected with unequal probabilities of being selected. Sampling weight values must be non-negative real numbers. If the sum of the sampling weights is not equal to the total number of observations in the analysis data set, the weights are rescaled so that they sum to the total number of observations. Sampling weights are available for all analysis types. Sampling weights are available for ESTIMATOR=MLR, MLM, MLMV, WLS, WLSM, WLSMV, and ULS. There are two exceptions. They are not available for WLS when all dependent variables are continuous and are not available for MLM or MLMV for EFA. Following is an example of how the WEIGHT option is used to identify a sampling weight variable:
WEIGHT IS sampwgt;
where sampwgt is the variable that contains sampling weight information.
The WTSCALE option is used with TYPE=TWOLEVEL to adjust the weight variable named using the WEIGHT option. With TYPE=TWOLEVEL, the WEIGHT option is used to identify the variable that contains within-level sampling weight information.
The WTSCALE option has the following settings: UNSCALED, CLUSTER, and ECLUSTER. CLUSTER is the default.
The UNSCALED setting uses the within weights from the data set with no adjustment. The CLUSTER setting scales the within weights from the data set so that they sum to the sample size in each cluster. The ECLUSTER setting scales the within weights from the data so that they sum to the effective sample size (Pothoff, Woodbury, & Manton, 1992).
The WTSCALE option is specified as follows:
WTSCALE = ECLUSTER;
where scaling the within weights so that they sum to the effective sample size is chosen.
BWEIGHT
The BWEIGHT option is used with TYPE=TWOLEVEL to identify the variable that contains between-level sampling weight information.
The BWEIGHT option is specified as follows:
BWEIGHT = bweight;
where bweight is the variable that contains between-level sampling weight information.
The B2WEIGHT option is used with TYPE=THREELEVEL to identify the variable that contains level 2 sampling weight information. Sampling weights are not available for TYPE=CROSSCLASSIFIED.
The B2WEIGHT option is specified as follows:
B2WEIGHT = b2weight;
where b2weight is the variable that contains level 2 sampling weight information.
The B3WEIGHT option is used with TYPE=THREELEVEL to identify the variable that contains level 3 sampling weight information. Sampling weights are not available for TYPE=CROSSCLASSIFIED.
The B3WEIGHT option is specified as follows:
B3WEIGHT = b3weight;
where b3weight is the variable that contains level 3 sampling weight information.
The BWTSCALE option is used in with TYPE=TWOLEVEL to adjust the between-level sampling weight variable named using the BWEIGHT option. The BWTSCALE option is used in with TYPE=THREELEVEL to adjust the level 2 and level 3 sampling weight variables named using the B2WEIGHT and B3WEIGHT options.
The BWTSCALE option has the following settings: UNSCALED and SAMPLE. SAMPLE is the default.
The UNSCALED setting uses the between weights from the data set with no adjustment. The SAMPLE option adjusts the between weights so that the product of the between and the within weights sums to the total sample size.
The BWTSCALE option is specified as follows:
BWTSCALE = UNSCALED;
where no adjustment is made to the between weights.
REPWEIGHTS
Replicate weights summarize information about a complex sampling design (Korn & Graubard, 1999; Lohr, 1999). They are used to properly estimate standard errors of parameter estimates. Replicate weights are available for TYPE=COMPLEX for continuous variables using maximum likelihood estimation and for binary, ordered categorical, and censored variables using weighted least squares estimation. The SUBPOPULATION option is not available with replicate weights. Replicate weights can be used or generated. When they are generated, they can be used in the analysis and/or saved (Asparouhov & Muthén, 2009b).
The REPWEIGHTS option is used to identify the replicate weight variables. The STRATIFICATION and CLUSTER options may not be used in conjunction with the REPWEIGHTS option. The WEIGHT option must be used. Following is an example of how to specify the REPWEIGHTS option:
REPWEIGHTS = rweight1-rweight80;
where rweight1 through rweight80 are replicate weight variables.
USING REPLICATE WEIGHTS
When existing replicate weights are used, the REPWEIGHTS option of the VARIABLE command is used in conjunction with the WEIGHT option of the VARIABLE command and the REPSE option of the ANALYSIS command. The sampling weights are used in the estimation of parameter estimates. The replicate weights are used in the estimation of standard errors of parameter estimates. The REPSE option specifies the resampling method that is used in the computation of the standard errors.
GENERATING REPLICATE WEIGHTS
When replicate weights are generated, the REPSE option of the ANALYSIS command and the WEIGHT option of the VARIABLE command along with the CLUSTER and/or the STRATIFICATION options of the VARIABLE command are used.
The SUBPOPULATION option is used with TYPE=COMPLEX to select observations for an analysis when a subpopulation (domain) is analyzed. If the SUBPOPULATION option is used, the USEOBSERVATIONS option cannot be used. When the SUBPOPULATION option is used, all observations are included in the analysis although observations not in the subpopulation are assigned weights of zero (see Korn & Graubard, 1999, pp. 207-211). The SUBPOPULATION option is not available for multiple group analysis.
The SUBPOPULATION option identifies those observations for analysis that satisfy the conditional statement specified after the equal sign and assigns them non-zero weights. For example, the following statement identifies observations with the variable gender equal to 2:
SUBPOPULATION = gender EQ 2;
Only variables from the NAMES statement of the VARIABLE command can be used in the conditional statement of the SUBPOPULATION option. Logical operators, not arithmetic operators, must be used in the conditional statement. Following are the logical operators that can be used in the conditional statement of the SUBPOPULATION option:
AND logical and
OR logical or
NOT logical not
EQ equal ==
NE not equal /=
GE greater than or equal to >=
LE less than or equal to <=
GT greater than >
LT less than <
As shown above, some of the logical operators can be referred to in two different ways. For example, equal can be referred to as EQ or ==.
For TYPE=COMPLEX, the FINITE option is used to identify the variable that contains the finite population correction factor, the sampling fraction, or the population size for each stratum. If the sampling fraction or the population size for each stratum is provided, these are used to compute the finite population correction factor. The finite population correction factor is used to adjust standard errors when clusters have been sampled without replacement (WOR) from strata in a finite population. The finite population correction factor is equal to one minus the sampling fraction. The sampling fraction is equal to the number of sampled clusters in a stratum divided by the number of clusters in the population for that stratum. The population size for each stratum is the number of clusters in the population for that stratum. The FINITE option is not available with replicate weights.
The FINITE option has three settings: FPC, SFRACTION, and POPULATION. FPC is used when the finite population correction factor is provided. SFRACTION is used when the sampling fraction is provided. POPULATION is used when the population size for each stratum is provided. FPC is the default. Following is an example of how the FINITE option is used to identify a finite population correction variable:
FINITE IS sampfrac (SFRACTION);
where sampfrac is the variable that contains the sampling fraction for each stratum.
MIXTURE MODELS
There are three options that are used specifically for mixture models. They are CLASSES, KNOWNCLASS, and TRAINING.
The CLASSES option is used to assign names to the categorical latent variables in the model and to specify the number of latent classes in the model for each categorical latent variable. This option is required for TYPE=MIXTURE. Between-level categorical latent variables must be identified as between-level variables using the BETWEEN option.
Following is an example of how the CLASSES option is used:
CLASSES = c1 (2) c2 (2) c3 (3);
where c1, c2, and c3 are the names of the three categorical latent variables in the model. The numbers in parentheses specify the number of classes for each categorical latent variable in the model. The categorical latent variable c1 has two classes, c2 has two classes, and c3 has three classes.
When there is more than one categorical latent variable in the model, there are rules related to the order of the categorical latent variables. The order is taken from the order of the categorical latent variables in the CLASSES statement. Because of the order in the CLASSES statement above, c1 is not allowed to be regressed on c2 in the model. It is only possible to regress c2 on c1 and c3 on c2 or c1. This order restriction does not apply to PARAMETERIZATION=LOGLINEAR.
The KNOWNCLASS option is used for multiple group analysis with TYPE=MIXTURE. The KNOWNCLASS option is used to identify the categorical latent variable for which latent class membership is known and equal to observed groups in the sample. Only one KNOWNCLASS variable can be used. Following is an example of how to specify the KNOWNCLASS option:
KNOWNCLASS = c1 (gender = 0 1);
where c1 is a categorical latent variable named and defined using the CLASSES option. The information in parentheses following the categorical latent variable name defines the known classes using an observed variable. In this example, the observed variable gender is used to define the known classes. The first class consists of individuals with the value 0 on the variable gender. The second class consists of individuals with the value 1 on the variable gender.
Following is an example with many known classes that uses the list function:
KNOWNCLASS = c (country = 101-110 112 113-115);
where c is a categorical latent variable named and defined using the CLASSES option. The information in parentheses following the categorical latent variable name defines the known classes using an observed variable. In this example, the observed variable country is used to define the known classes. The first class consists of individuals with the value 101 on the variable country. The last class consists of individuals with the value 115 on the variable country. There are a total of 14 classes.
The KNOWNCLASS option can be specified by mentioning only the name of the observed variable that defines the known classes without giving the values of the observed variable:
KNOWNCLASS = c (country);
where c is a categorical latent variable named and defined using the CLASSES option. In this example, the observed variable country is used to define the known classes. The number of known classes is taken from the CLASSES option. The values of the variable country are taken from the data. The first class consists of individuals with the lowest value on the variable country. The last class consists of individuals with the highest value on the variable country.
The TRAINING option is used to identify the variables that contain information about latent class membership and specify whether the information is about class membership, probability of class membership, or priors of class membership. The TRAINING option has three settings: MEMBERSHIP, PROBABILITIES, and PRIORS. MEMBERSHIP is the default. Training variables can be variables from the NAMES statement of the VARIABLE command and variables created using the DEFINE command and the DATA transformation commands. This option is available only for models with a single categorical latent variable.
Following is an example of how the TRAINING option is used for an example with three latent classes where the training variables contain information about class membership:
TRAINING = t1 t2 t3;
where t1, t2, and t3 are variables that contain information about latent class membership. The variable t1 provides information about membership in class 1, t2 provides information about membership in class 2, and t3 provides information about membership in class 3. An individual is allowed to be in any class for which they have a value of one on a training variable. An individual who is known to be in class 2 would have values of 0, 1, and 0 on t1, t2, and t3, respectively. An individual with unknown class membership would have the value of 1 on t1, t2, and t3. An alternative specification is:
TRAINING = t1 t2 t3 (MEMBERSHIP);
Fractional values can be used to provide information about the probability of class membership when class membership is not estimated but is fixed at fractional values for each individual. For example, an individual who has a probability of .9 for being in class 1, .05 for being in class 2, and .05 for being in class 3 would have t1=.9, t2=.05, and t3=.05. Fractional training data must sum to one for each individual.
Following is an example of how the TRAINING option is used for an example with three latent classes where the training variables contain information about probabilities of class membership:
TRAINING = t1 t2 t3 (PROBABILITIES);
where t1, t2, and t3 are variables that contain information about the probability of latent class membership. The variable t1 provides information about the probability of membership in class 1, t2 provides information about the probability of membership in class 2, and t3 provides information about the probability of membership in class 3.
Priors can be used when individual class membership is not known but when information is available on the probability of an individual being in a certain class. For example, an individual who has a probability of .9 for being in class 1, .05 for being in class 2, and .05 for being in class 3 would have t1=.9, t2=.05, and t3=.05. Prior values must sum to one for each individual.
Following is an example of how the PRIORS option is used for an example with three latent classes where the training variables contain information about priors of class membership:
TRAINING = t1 t2 t3 (PRIORS);
where t1, t2, and t3 are variables that contain information about the probability of being in a certain class. The variable t1 provides information about the probability of membership in class 1, t2 provides information about the probability of membership in class 2, and t3 provides information about the probability of membership in class 3.
MULTILEVEL MODELS
There are two options specific to multilevel models. They are WITHIN and BETWEEN. Variables identified using the WITHIN and BETWEEN options can be variables from the NAMES statement of the VARIABLE command and variables created using the DEFINE command and the DATA transformation commands.
The WITHIN option is used with TYPE=TWOLEVEL, TYPE=THREELEVEL, and TYPE=CROSSCLASSIFIED to identify the variables in the data set that are measured on the individual level and to specify the levels on which they are modeled. All variables on the WITHIN list must be measured on the individual level. An individual-level variable can be modeled on all or some levels.
For TYPE=TWOLEVEL, an individual-level variable can be modeled on only the within level or on both the within and between levels. If a variable measured on the individual level is mentioned on the WITHIN list, it is modeled on only the within level. It has no variance in the between part of the model. If it is not mentioned on the WITHIN list, it is modeled on both the within and between levels. The WITHIN option is specified as follows:
WITHIN = y1 y2 x1;
where y1, y2, and x1 are variables measured on the individual level and modeled on only the within level.
For TYPE=THREELEVEL, an individual-level variable can be modeled on only level 1, on levels 1 and 2, levels 1 and 3, or on all levels. Consider a model where students are nested in classrooms and classrooms are nested in schools. Level 1 is student; level 2 is classroom; and level 3 is school. If a variable measured on the individual level is mentioned on the WITHIN list without a label, it is modeled on only level 1. It has no variance on levels 2 and 3. If it is mentioned on the WITHIN list with a level 2 cluster label, it is modeled on levels 1 and 2. It has no variance on level 3. If it is mentioned on the WITHIN list with a level 3 cluster label, it is modeled on levels 1 and 3. It has no variance on level 2. If it is not mentioned on the WITHIN list, it is modeled on all levels.
Following is an example of how to specify the WITHIN option for TYPE=THREELEVEL:
WITHIN = y1-y3 (class) y4-y6 (school) y7-y9;
In the example, y1, y2, and y3 are variables measured on the individual level and modeled on only level 1, student. Variables modeled on only level 1 must precede variables modeled on the other levels. Y4, y5, and y6 are variables measured on the individual level and modeled on level 1, student, and level 2, class, where class is the level 2 cluster variable. Y7, y8, and y9 are variables measured on the individual level and modeled on level 1, student, and level 3, school, where school is the level 3 cluster variable.
An alternative specification of the WITHIN option above reverses the order of the level 2 and level 3 variables:
WITHIN = y1-y3 (school) y7-y9 (class) y4-y6;
Variables modeled on only level 1 must precede variables modeled on the other levels. Another alternative specification is:
WITHIN = y1-y3;
WITHIN = (class) y4-y6;
WITHIN = (school) y7-y9;
In this specification, the WITHIN statement for variables modeled on only level 1 must precede the other WITHIN statements. The order of the other WITHIN statements does not matter.
For TYPE=CROSSCLASSIFIED, an individual-level variable can be modeled on only level 1, on levels 1 and 2a, levels 1 and 2b, or on all levels. Consider a model where students are nested in schools crossed with neighborhoods. Level 1 is student; level 2a is school; and level 2b is neighborhood. If a variable measured on the individual level is mentioned on the WITHIN list without a label, it is modeled on only level 1. It has no variance on levels 2a and 2b. If it is mentioned on the WITHIN list with a level 2a cluster label, it is modeled on levels 1 and 2a. It has no variance on level 2b. If it is mentioned on the WITHIN list with a level 2b cluster label, it is modeled on levels 1 and 2b. It has no variance on level 2a. If it is not mentioned on the WITHIN list, it is modeled on all levels.
Following is an example of how to specify the WITHIN option for TYPE=CROSSCLASSIFIED:
WITHIN = y1-y3 (school) y4-y6 (neighbor) y7-y9;
In the example, y1, y2, and y3 are variables measured on the individual level and modeled on only level 1, student. Variables modeled on only level 1 must precede variables modeled on the other levels. Y4, y5, and y6 are variables measured on the individual level and modeled on level 1, student, and level 2a, school, where school is the level 2a cluster variable. Y7, y8, and y9 are variables measured on the individual level and modeled on level 1, student, and level 2b, neighborhood, where neighborhood is the level 2b cluster variable.
The BETWEEN option is used with TYPE=TWOLEVEL, TYPE=THREELEVEL, and TYPE=CROSSCLASSIFIED to identify the variables in the data set that are measured on the cluster level(s) and to specify the level(s) on which they are modeled. All variables on the BETWEEN list must be measured on a cluster level. A cluster-level variable can be modeled on all or some cluster levels.
For TYPE=TWOLEVEL, a cluster-level variable can be modeled on only the between level. The BETWEEN option is specified as follows:
BETWEEN = z1 z2 x1;
where z1, z2, and x1 are variables measured on the cluster level and modeled on the between level. The BETWEEN option is also used to identify between-level categorical latent variables with TYPE=TWOLEVEL MIXTURE.
For TYPE=THREELEVEL, a variable measured on level 2 can be modeled on only level 2 or on levels 2 and 3. A variable measured on level 3 can be modeled on only level 3. Consider a model where students are nested in classrooms and classrooms are nested in schools. Level 1 is student; level 2 is classroom; and level 3 is school. If a variable measured on level 2 is mentioned on the BETWEEN list without a label, it is modeled on levels 2 and 3. If a variable measured on level 2 is mentioned on the BETWEEN list with a level 2 cluster label, it is modeled on only level 2. It has no variance on level 3. A variable measured on level 3 must be mentioned on the BETWEEN list with a level 3 cluster label. Following is an example of how to specify the BETWEEN option for TYPE=THREELEVEL:
BETWEEN = y1-y3 (class) y4-y6 (school) y7-y9;
In this example, y1, y2, and y3 are cluster-level variables measured on level 2, class, and modeled on both levels 2 and 3. Variables modeled on both levels 2 and 3 must precede variables modeled on only level 2 or level 3. Y4, y5, and y6 are cluster-level variables measured on level 2, class, and modeled on level 2. Y7, y8, and y9 are cluster-level variables measured on level 3 and modeled on level 3.
An alternative specification of the BETWEEN option above reverses the order of the level 2 and level 3 variables:
BETWEEN = y1-y3 (school) y7-y9 (class) y4-y6;
Variables modeled on both levels 2 and 3 must precede variables modeled on only level 2 or level 3. Another alternative specification is:
BETWEEN = y1-y3;
BETWEEN = (class) y4-y6;
BETWEEN = (school) y7-y9;
In this specification, the BETWEEN statement for variables modeled on both levels 2 and 3 must precede the other BETWEEN statements. The order of the other BETWEEN statements does not matter.
For TYPE=CROSSCLASSIFIED, a variable measured on level 2a must be mentioned on the BETWEEN list with a level 2a cluster label. It can be modeled on only level 2a. A variable measured on level 2b must be mentioned on the BETWEEN list with a level 2b cluster label. It can be modeled on only level 2b. Consider a model where students are nested in schools crossed with neighborhoods. Level 1 is student; level 2a is school; and level 2b is neighborhood. Following is an example of how to specify the BETWEEN option for TYPE=CROSSCLASSIFIED:
BETWEEN = (school) y1-y3 (neighbor) y4-y6;
In this example, y1, y2, and y3 are cluster-level variables measured on level 2a, school, and modeled on only level 2a. Y4, y5, and y6 are cluster-level variables measured on level 2b, neighborhood, and modeled on only level 2b.
CONTINUOUS-TIME SURVIVAL MODELS
There are two options specific to continuous-time survival models. They are SURVIVAL and TIMECENSORED. Variables identified using the SURVIVAL and TIMECENSORED options can be variables from the NAMES statement of the VARIABLE command and variables created using the DEFINE command and the DATA transformation commands.
The SURVIVAL option is used to identify the variables that contain information about time to event and to provide information about the number and lengths of the time intervals in the baseline hazard function to be used in the analysis. The SURVIVAL option must be used in conjunction with the TIMECENSORED option. The SURVIVAL option can be specified in five ways: the default baseline hazard function, a non-parametric baseline hazard function, a semi-parametric baseline hazard function, a parametric baseline hazard function, and a constant baseline hazard function.
The SURVIVAL option is specified as follows when using the default baseline hazard function:
SURVIVAL = t;
where t is the variable that contains time-to-event information. The default is either a semi-parametric baseline hazard function with ten time intervals or a non-parametric baseline hazard function. The default is a semi-parametric baseline hazard function with ten time intervals for models where t is regressed on a continuous latent variable, for multilevel models, and for models that require Monte Carlo numerical integration. In this case, the lengths of the time intervals are selected internally in a non-parametric fashion. For all other models, the default is a non-parametric baseline hazard function as in Cox regression where the number and lengths of the time intervals are taken from the data and the baseline hazard function is saturated.
The SURVIVAL option is specified as follows when using a non-parametric baseline hazard function as in Cox regression:
SURVIVAL = t (ALL);
where t is the variable that contains time-to-event information and ALL is a keyword that specifies that the number and lengths of the time intervals are taken from the data and the baseline hazard is saturated. It is not recommended to use the keyword ALL when the BASEHAZARD option of the ANALYSIS command is ON because it results in a large number of baseline hazard parameters.
The SURVIVAL option is specified as follows when using a semi-parametric baseline hazard:
SURVIVAL = t (10);
where t is the variable that contains time-to-event information. The number in parentheses specifies that 10 intervals are used in the analysis where the lengths of the time intervals are selected internally in a non-parametric fashion.
The SURVIVAL option is specified as follows when using a parametric baseline hazard function:
SURVIVAL = t (4*5 1*10);
where t is the variable that contains time-to-event information. The numbers in parentheses specify that four time intervals of length five and one time interval of length ten are used in the analysis.
The SURVIVAL option is specified as follows when using a constant baseline hazard function:
SURVIVAL = t (CONSTANT);
where t is the variable that contains time-to-event information and CONSTANT is the keyword that specifies a constant baseline hazard function.
The TIMECENSORED option is used in conjunction with the SURVIVAL option to identify the variables that contain information about right censoring, for example, when an individual leaves a study or when an individual has not experienced the event before the study ends. There must be the same number and order of variables in the TIMECENSORED option as there are in the SURVIVAL option. The variables that contain information about right censoring must be coded so that zero is not censored and one is right censored. If they are not, this can be specified as part of the TIMECENSORED option. The TIMECENSORED option is specified as follows when the variable is coded zero for not censored and one for right censored:
TIMECENSORED = tc;
The TIMECENSORED option is specified as follows when the variable is not coded zero for not censored and one for right censored:
TIMECENSORED = tc (1 = NOT 999 = RIGHT);
The value one is automatically recoded to zero and the value 999 is automatically recoded to one.
The LAGGED option is used in time series analysis to specify the maximum lag to use for an observed variable during model estimation. Following is an example of how to specify the LAGGED option:
LAGGED = y (1);
where y is the variable in a time series analysis and the number 1 in parentheses is the maximum lag that will be used in model estimation. The lagged variable is referred to in the MODEL command by adding to the name of the variable an ampersand (&) and the number of the lag. The variable y at lag one is referred to as y&1.
Following is an example of how to specify a maximum lag of 2 for a set of variables:
LAGGED = y1-y3 (2);
where y1, y2, and y3 are variables in a time series analysis and the number 2 in parentheses is the maximum lag that will be used in model estimation. The lagged variables are referred to in the MODEL command by adding to the name of the variable an ampersand (&) and the number of the lag. The variable y1 at lag one is referred to as y1&1. The variable y1 at lag two is referred to as y1&2.
The TINTERVAL option is used in time series analysis to specify the time interval that is used to create a time variable when data are misaligned with respect to time due to missed measurement occasions that are not assigned a missing value flag and when measurement occasions are random. The data set must be sorted by the time interval variable.
The time interval value represents the difference in time between two consecutive measurement occasions. Using this value and the lowest value of the time interval variable, intervals are created that are used to create a time variable. The first interval is the lowest value of the time interval variable plus/minus half of the time interval value. The second interval adds the time interval value to the values of the first interval etc.. All values of the time interval variable that fall into the same interval are given the same value on the time variable. If an interval does not contain a value, a missing value flag is assigned. Following is an example of how to specify the TINTERVAL option:
TINTERVAL = time (1);
where time is the time interval variable and the value one is the time interval value. If the lowest time interval variable value is one, the first three intervals are .5 to 1.5, 1.5 to 2.5, and 2.5 to 3.5. The first three time variable values are 1, 2, and 3. For further details, see Asparouhov, Hamaker, and Muthén (2017).
The DEFINE command is used to transform existing variables and to create new variables. It includes several options for transforming variables including a do loop for repeating statements. The operations available in DEFINE can be executed for all observations or selectively using conditional statements. Transformations of existing variables do not affect the original data but only the data used for the analysis. If analysis data are saved using the SAVEDATA command, the transformed values rather than the original values are saved.
The statements in the DEFINE command are executed one observation at a time in the order specified with one exception. The CLUSTER_MEAN, CENTER, and STANDARDIZE options are executed in the order mentioned after all transformations specified before them in the DEFINE command and the DATA transformation commands are executed. All statements specified after these options are then executed one observation at a time in the order specified. These transformations use the new values from the CLUSTER_MEAN, CENTER, and STANDARDIZE options where applicable. For example, if two variables are centered and an interaction between them is specified after the CENTER option, the interaction uses the centered variables. Any variable listed in the NAMES option of the VARIABLE command or created in the DEFINE command can be transformed or used to create new variables. New variables created in the DEFINE command that will be used in an analysis must be listed on the USEVARIABLES list after the original variables. All statements specified after the CLUSTER_MEAN, CENTER and STANDARDIZE options must refer to variables used in the analysis that are listed on the USEVARIABLES list.
Following are examples of the types of transformations available:
|
DEFINE: |
|
|
|
|
|
|
|
|
variable = mathematical expression;
|
|
|
|
IF (conditional statement) THEN transformation statements;
|
|
|
|
_MISSING |
|
|
|
variable = MEAN (list of variables); |
|
|
|
variable = SUM (list of variables); |
|
|
|
CUT variable or list of variables (cutpoints); |
|
|
|
variable = CLUSTER_MEAN (variable); |
|
|
|
CENTER variable or list of variables (GRANDMEAN); CENTER variable or list of variables (GROUPMEAN); CENTER variable or list of variables (GROUPMEAN label); |
|
|
|
STANDARDIZE variable or list of variables; |
|
|
|
DO (number, number) expression; DO ($, number, number) DO (#, number, number) expression; |
|
DEFINE is not a required command.
LOGICAL OPERATORS, ARITHMETIC OPERATORS, AND FUNCTIONS
The following logical operators can be used in DEFINE:
AND logical and
OR logical or
NOT logical not
EQ = = equal
NE /= not equal
GE >= greater than or equal to
LE <= less than or equal to
GT > greater than
LT < less than
As shown above, some of the logical operators can be referred to in two different ways. For example, equal can be referred to as EQ or = =.
The following arithmetic operations can be used in DEFINE:
+ addition y + x;
- subtraction y - x;
* multiplication y * x;
/ division y / x;
** exponentiation y**2;
% remainder remainder of y/x;
The following functions can be used in DEFINE:
LOG base e log LOG (y);
LOG10 base 10 log LOG10 (y);
EXP exponential EXP (y);
SQRT square root SQRT (y);
ABS absolute value ABS(y);
SIN sine SIN (y);
COS cosine COS (y);
TAN tangent TAN(y);
ASIN arcsine ASIN (y);
ACOS arccosine ACOS (y);
ATAN arctangent ATAN (y);
PHI standard normal PHI (y); PHI (#);
distribution function
When a non-conditional statement is used to transform existing variables or create new variables, the variable on the left-hand side of the equal sign is assigned the value of the expression on the right-hand side of the equal sign, for example,
y = y/100;
transforms the original variable y by dividing it by 100. Non-conditional statements can be used to create new variables, for example,
abuse = item1 + item2 + item8 + item9;
An individual with a missing value on any variable used on the right-hand side of the equal sign is assigned a missing value on the variable on the left-hand side of the equal sign.
CONDITIONAL STATEMENTS
Conditional statements can also be used to transform existing variables and to create new variables. Conditional statements take the following form:
IF (gender EQ 1 AND ses EQ 1) THEN group = 1;
IF (gender EQ 1 AND ses EQ 2) THEN group = 2;
IF (gender EQ 1 AND ses EQ 3) THEN group = 3;
IF (gender EQ 2 AND ses EQ 1) THEN group = 4;
IF (gender EQ 2 AND ses EQ 2) THEN group = 5;
IF (gender EQ 2 AND ses EQ 3) THEN group = 6;
An individual with a missing value on any variable used in the conditional statement is assigned a missing value on the new variable. If no value is specified for a condition, individuals with that condition are assigned a missing value.
The _MISSING keyword can be used in DEFINE to refer to missing values. The _MISSING keyword can be used to assign a missing value to a variable, for example,
IF (y EQ 0) THEN u = _MISSING;
It can also be used as part of the condition, for example,
IF (y EQ _MISSING) THEN u = 1;
OPTIONS FOR DATA TRANSFORMATION
The DEFINE command has six options for data transformation. The first option creates a variable that is the average of a set of variables. The second option creates a variable that is the sum of a set of variables. The third option categorizes one or several variables using the same set of cutpoints. The fourth option creates a variable that is the average for each cluster of an individual-level variable. The fifth option centers a variable by subtracting the grand mean or group mean from each value. The sixth option standardizes a variable to have a mean of zero and a standard deviation of one.
The MEAN option is used to create a variable that is the average of a set of variables. It is specified as follows:
mean = MEAN (y1 y3 y5);
where the variable mean is the average of variables y1, y3, and y5. Averages are based on the set of variables with no missing values. Any observation that has a missing value on all of the variables being averaged is assigned a missing value on the mean variable.
The list function can be used with the MEAN option as follows:
ymean = MEAN (y1-y10);
where the variable ymean is the average of variables y1 through y10.
Variables used with the MEAN option must be original variables from the NAMES statement of the VARIABLE command or temporary variables created using the DEFINE command. The order of the variables for the list function is taken from the NAMES statement not the USEVARIABLES statement.
The SUM option is used to create a variable that is the sum of a set of variables. It is specified as follows:
sum = SUM (y1 y3 y5);
where the variable sum is the sum of variables y1, y3, and y5. Any observation that has a missing value on one or more of the variables being summed is assigned a missing value on the sum variable.
The list function can be used with the SUM option as follows:
ysum = SUM (y1-y10);
where the variable ysum is the sum of variables y1 through y10.
Variables used with the SUM option must be original variables from the NAMES statement of the VARIABLE command or temporary variables created using the DEFINE command. The order of the variables for the list function is taken from the NAMES statement not the USEVARIABLES statement.
The CUT option categorizes a variable or list of variables using the same set of cutpoints. More than one CUT statement can be included in the DEFINE command. Following is an example of how the CUT option is used:
CUT y1 y5-y7 (30 40);
This statement results in the variables y1, y5, y6, and y7 having three categories: less than or equal to 30, greater than 30 and less than or equal to 40, and greater than 40, with values of 0, 1, and 2, respectively. Any observation that has a missing value on a variable that is being cut is assigned a missing value on the cut variable.
Variables used with the CUT option must be original variables from the NAMES statement of the VARIABLE command or temporary variables created using the DEFINE command. The order of the variables for the list function is taken from the NAMES statement not the USEVARIABLES statement.
The CLUSTER_MEAN option is used with TYPE=TWOLEVEL and TYPE=COMPLEX along with the CLUSTER option to create a variable that is the average of the values of an individual-level variable for each cluster. In multiple group analysis, each group’s means are used for creating cluster means in that group. It is specified as follows:
clusmean = CLUSTER_MEAN (x);
where the variable clusmean is the average of the values of x for each cluster. Averages are based on the set of non-missing values for the observations in each cluster. Any cluster for which all observations have missing values is assigned a missing value on the cluster mean variable.
All transformations specified in the DATA transformation commands or before the CLUSTER_MEAN option in the DEFINE command use the original values of the variables. All transformations specified in the DEFINE command after the CLUSTER_MEAN option use the cluster-mean values of the variables. To be used with the CLUSTER_MEAN option, any new variables created using the DEFINE command must be placed on the USEVARIABLES list after the original variables. The order of the variables for the list function is taken from the USEVARIALES list. If there is not USEVARIABLES list, the order of the variables is taken from the NAMES list.
The CENTER option is used to center continuous observed variables by subtracting the grand mean or group mean from each variable. In multiple group analysis, each group’s means are used for centering in that group. Grand-mean centering is available for all analyses. Group-mean centering is available with TYPE=TWOLEVEL, TYPE=THREELEVEL, TYPE=CROSSCLASSIFIED, and TYPE=COMPLEX in conjunction with the CLUSTER option. The CENTER option has two settings: GRANDMEAN and GROUPMEAN.
All transformations that are specified in the DATA transformation commands or before the CENTER option in the DEFINE command use the original values of the variables. All transformations that are specified in the DEFINE command after the CENTER option use the centered values of the variables. To be used with the CENTER option, any new variables created using the DEFINE command must be placed on the USEVARIABLES list after the original variables. The order of variables for the list function is taken from the USEVARIABLES list. If there is no USEVARIABLES list, the order of the variables is taken from the NAMES list. Any observation that has a missing value on the variable to be centered is assigned a missing value on the centered variable.
GRANDMEAN
Grand-mean centering subtracts the overall mean from a variable. Grand-mean centering is available for all continuous observed variables used in an analysis. Following is an example of how to specify grand-mean centering for TYPE=TWOLEVEL and TYPE=COMPLEX:
CENTER x1-x4 (GRANDMEAN);
where x1, x2, x3, and x4 are the variables to be centered using the overall means for these variables.
For TYPE=THREELEVEL, there are three types of grand-mean centering. Consider a model where students are nested in classrooms and classrooms are nested in schools. Level 1 is student; level 2 is classroom; and level 3 is school. For variables modeled on level 1 and higher, grand-mean centering subtracts the overall mean from a variable. For variables modeled on level 2 and higher, grand-mean centering subtracts the cluster 1, classroom, mean from a variable. For variables modeled on level 3, grand-mean centering subtracts the cluster 2, school, mean from a variable.
Following is an example of how to specify grand-mean centering for TYPE=THREELEVEL:
CENTER x1-x4 (GRANDMEAN);
where x1, x2, x3, and x4 are the variables to be centered using the overall means for variables modeled on level 1 and higher, the cluster 1 means for variables modeled on level 2 and higher, and the cluster 2 means for variables modeled on level 3 and higher.
For TYPE=CROSSCLASSIFIED, there are three types of grand-mean centering. Consider a model where students are nested in schools crossed with neighborhoods. Level 1 is student; level 2a is school; and level 2b is neighborhood. For variables modeled on level 1 and higher, grand-mean centering subtracts the overall mean from a variable. For variables modeled on level 2a, grand-mean centering subtracts the cluster 2a, school, mean from a variable. For variables modeled on level 2b, grand-mean centering subtracts the cluster 2b, neighborhood, mean from a variable.
Following is an example of how to specify grand-mean centering for TYPE=CROSSCLASSIFIED:
CENTER x1-x4 (GRANDMEAN);
where x1, x2, x3, and x4 are the variables to be centered using the overall means for variables modeled on level 1 and higher, the cluster 2a means for variables modeled on level 2a, and the cluster 2b means for variables modeled on level 2b.
GROUPMEAN
For TYPE=TWOLEVEL and TYPE=COMPLEX, group-mean centering subtracts the cluster mean from a variable. For TYPE=COMPLEX, group-mean centering is available for all continuous observed variables in an analysis. For TYPE=TWOLEVEL, group-mean centering is available for all continuous observed variables used in an analysis that are not modeled at the highest level. Following is an example of how to specify group-mean centering:
CENTER x1-x4 (GROUPMEAN);
where x1, x2, x3, and x4 are the variables to be centered using the cluster means for these variables.
For TYPE=THREELEVEL, group-mean centering is available for any continuous observed variable that is not modeled at the highest level. Consider a model where students are nested in classrooms and classrooms are nested in schools. Level 1 is student; level 2 is classroom; and level 3 is school. For variables modeled on levels 1 and 2 and for variables modeled on only level 2, group-mean centering subtracts the cluster 2, school, mean from a variable where the cluster 2 mean is the average of the cluster 1, class, means for each level 3, school, cluster. Following is an example of how to specify cluster 2 group-mean centering:
CENTER x1-x4 (GROUPMEAN school);
where school is the cluster 2 variable and x1, x2, x3, and x4 are the variables to be centered using cluster 2 means for these variables.
For variables modeled on only level 1, both cluster 1, classroom, and cluster 2, school, group-mean centering are available. Following is an example of how to specify group-mean centering using cluster 1 and cluster 2 means:
CENTER x1-x2 (GROUPMEAN class);
CENTER x3 x4 (GROUPMEAN school);
In this example, class is the cluster 1 variable and x1 and x2 are the variables to be centered using cluster 1 means for these variables. School is the cluster 2 variable and x3 and x4 are the variables to be centered using cluster 2 means for these variables. A variable cannot be centered using both cluster 1 and cluster 2 means.
For TYPE=CROSSCLASSIFIED, group-mean centering is available for any continuous observed variable that is not modeled at the highest level. Consider a model where students are nested in schools crossed with neighborhoods. Level 1 is student; level 2a is school; and level 2b is neighborhood. For variables modeled on only level 1, group-mean centering subtracts the cluster 2a, school, mean or the cluster 2b, neighborhood mean from a variable. Following is an example of how to specify cluster 2a and 2b group-mean centering:
CENTER x1-x4 (GROUPMEAN school);
CENTER x5-x8 (GROUPMEAN neighbor);
In this example, school is the cluster 2a variable and x1, x2, x3, and x4 are the variables to be centered using cluster 2a means for these variables. Neighbor is the cluster 2b variable and x5, x6, x7, and x8 are the variables to be centered using the cluster 2b means for these variables.
The STANDARDIZE option is used to standardize continuous variables by subtracting the mean from each value and dividing each value by the standard deviation. In multiple group analysis, each group’s means are used for standardizing in that group. Following is an example of how the STANDARDIZE option is used:
STANDARDIZE y1 y5-y10 y14;
where the variables y1, y5 through y10, and y14 will be standardized. Any observation that has a missing value on the variable to be standardized is assigned a missing value on the standardized variable.
All transformations that are specified in the DATA transformation commands or before the STANDARDIZE option in the DEFINE command use the original values of the variables. All transformations that are specified in the DEFINE command after the STANDARDIZE option use the standardized values of the variables. To be used with the STANDARDIZE option, any new variables created using the DEFINE command must be placed on the USEVARIABLES list after the original variables. The order of variables for the list function is taken from the USEVARIABLES list. If there is no USEVARIABLES list, the order is taken from the NAMES list.
The DO option provides a do loop and a double do loop to facilitate specifying the same transformation for a set of variables. Following is an example of how to specify a do loop:
DO (1, 5) diff# = y# - x#;
where the numbers in parentheses give the range of values the do loop will use. The number sign (#) is replaced by these values during the execution of the do loop. Following are the transformations that are executed based on the DO option specified above:
diff1 = y1 - x1;
diff2 = y2 - x2;
diff3 = y3 - x3;
diff4 = y4 - x4;
diff5 = y5 - x5;
Following is an example of how to specify a double do loop where x1 is equal to 0.1 and x2 is equal to 2:
DO ($,1,2) DO (#,1,4) y$# = x$ * u#;
where the numbers in parentheses give the range of values the double do loop will use. The numbers replace the symbol preceding them. Following are the transformations that are executed based on the DO option specified above:
y11 = 0.1 * u1;
y12 = 0.1 * u2;
y13 = 0.1 * u3;
y14 = 0.1 * u4;
y21 = 2 * u1;
y22 = 2 * u2;
y23 = 2 * u3;
y24 = 2 * u4;