CHAPTER 17
MODEL COMMAND
In this chapter, the MODEL command is discussed. The MODEL command is used to describe the model to be estimated. The first part of this chapter describes the general modeling framework used by Mplus and introduces a set of terms that are used to describe the model to be estimated. The second part of this chapter explains how a model is translated into the Mplus language using the options of the MODEL command. The last part of the chapter describes variations of the MODEL command. The MODEL command has variations for use with models with indirect effects, models with linear and non-linear constraints, models with parameter constraints for the Wald test, multiple group models, mixture models, multilevel models, and models for generating data for Monte Carlo simulation studies.
There are three important distinctions that need to be made about the variables in an analysis in order to be able to specify a model. The distinctions are whether variables are observed or latent, whether variables are dependent or independent, and the scale of the observed dependent variables.
Two types of variables can be modeled: observed variables and latent variables. Observed variables are variables that are directly measured such as test scores and diagnostic criteria. They are sometimes referred to as manifest variables, outcomes, or indicators. Latent variables are variables that are not directly measured such as ability, depression, and health status. They are measured indirectly by a set of observed variables. There are two types of latent variables: continuous and categorical. Continuous latent variables are sometimes referred to as factors, dimension, constructs, or random effects. Categorical latent variables are sometimes referred to as latent class variables or mixtures.
DEPENDENT OR INDEPENDENT VARIABLES
Observed and latent variables can play the role of a dependent variable or an independent variable in the model. The distinction between dependent and independent variables is that of a regression analysis for y regressed on x where y is a dependent variable and x is an independent variable. An independent variable is one that is not influenced by any other variable. Dependent variables are those that are influenced by other variables. Other terms used for dependent variables are outcome variable, response variable, indicator variable, y variable, and endogenous variable. Other terms used for independent variables are covariate, background variable, explanatory variable, predictor, x variable, and exogenous variable.
SCALE OF OBSERVED DEPENDENT VARIABLES
The scale of observed dependent variables can be continuous, censored, binary, ordered categorical (ordinal), unordered categorical (nominal), counts, or combinations of these variable types.
The purpose of modeling data is to describe the structure of a data set in a simple way so that it is more understandable and interpretable. Essentially, modeling data amounts to specifying a set of relationships between variables.
The underlying model of Mplus consists of three parts: the measurement model for the indicators of the continuous latent variables, the measurement model for the indicators of the categorical latent variables, and the structural model involving the continuous and categorical latent variables and the observed variables that are not indicators of the continuous or categorical latent variables. A model may consist of only a measurement model as in confirmatory factor analysis or latent class analysis, only a structural model as in a path analysis, or both a measurement model and a structural model as in latent variable structural equation modeling, longitudinal growth modeling, regression mixture modeling, or growth mixture modeling.
The MODEL command is used to describe the model to be estimated. It has options for defining latent variables, describing relationships among variables in the model, and specifying details of the model. The MODEL command has variations for use with models with indirect effects, models with non-linear constraints, models with parameter constraints for the Wald test, multiple group models, mixture models, multilevel models, and models for generating data for Monte Carlo simulation studies.
Following are the options for the MODEL command:
|
MODEL: |
|
||
|
BY |
short for measured by -- defines latent variables example: f1 BY y1-y5; |
||
|
ON |
short for regressed on -- defines regression relationships example: f1 ON x1-x9; |
||
|
PON |
short for regressed on -- defines paired regression relationships example: f2 f3 PON f1 f2; |
||
|
WITH |
short for correlated with -- defines correlational relationships example: f1 WITH f2; |
||
|
PWITH |
short for correlated with -- defines paired correlational relationships example: f1 f2 f3 PWITH f4 f5 f6; |
||
|
list of variables; |
refers to variances and residual variances example: f1 y1-y9; |
||
|
[list of variables]; |
refers to means, intercepts, thresholds example: [f1, y1-y9]; |
||
|
* |
frees a parameter at a default value or a specific starting value example: y1* y2*.5; |
||
|
@ |
fixes a parameter at a default value or a specific value example: y1@ y2@0; |
||
|
(number) |
constrains parameters to be equal example: f1 ON x1 (1); f2 ON x2 (1); |
||
|
variable$number |
label for the threshold of a variable |
||
|
variable#number |
label for nominal observed or categorical latent variable |
||
|
variable#1 |
label for censored or count inflation variable |
||
|
variable#number |
label for baseline hazard parameters |
||
|
variable#number |
label for a latent class |
||
|
(name) |
label for a parameter |
||
|
{list of variables}; |
refers to scale factors example: {y1-y9}; |
||
|
|
growth model AT ON BY variable name XWITH |
used for growth models, random effects, and latent variable interactions example: i s | y1@0 y2@1 y3@2; example: i s | y1 y2 y3 AT t1 t2 t3; example: s | y1 ON x1; example: s1 s2 s3 | f BY y1 y2 y3; f@1; example: logv | y; example: int | f1 XWITH f2; |
||
|
MODEL INDIRECT:
IND
VIA
MOD |
describes indirect and total effects describes a specific indirect effect or a set of indirect effects when there is no moderation; describes a set of indirect effects that includes specific mediators; describes a specific indirect effect when there is moderation; |
|
|
|
MODEL CONSTRAINT: NEW DO PLOT LOOP |
describes linear and non-linear constraints on parameters assigns labels to parameters not in the analysis model; describes a do loop or double do loop; describes y-axis variables; describes x-axis variables; |
|
|
|
MODEL TEST:
DO |
describes testing restrictions on the analysis model using the Wald test describes a do loop or double do loop; |
|
|
|
MODEL PRIORS: COVARIANCE DO DIFFERENCE |
specifies the prior distribution for the parameters assigns a prior to the covariance between two parameters; describes a do loop or double do loop; assigns priors to differences between parameters; |
|
|
Following are variations of the MODEL command:
|
MODEL: |
describes the analysis model |
|
|
MODEL label: |
describes the group-specific model in multiple group analysis and the model for each categorical latent variable and combinations of categorical latent variables in mixture modeling |
|
|
MODEL: %OVERALL% %class label% |
describes the overall part of a mixture model describes the class-specific part of a mixture model |
|
|
MODEL: %WITHIN% %BETWEEN% %BETWEEN label% |
describes the individual-level model describes the cluster-level model for a two-level model describes the cluster-level model for a three-level or cross-classified model |
|
|
MODEL POPULATION: |
describes the data generation model |
|
|
MODEL POPULATION-label: |
describes the group-specific data generation model in multiple group analysis and the data generation model for each categorical latent variable in mixture modeling |
|
|
MODEL POPULATION: %OVERALL%
%class label% |
describes the overall data generation model for a mixture model describes the class-specific data generation model for a mixture model |
|
|
MODEL POPULATION: %WITHIN%
%BETWEEN%
%BETWEEN label% |
describes the individual-level data generation model for a multilevel model describes the cluster-level data generation model for a two-level model describes the cluster-level data generation model for a three-level or cross-classified model |
|
|
MODEL COVERAGE: |
describes the population parameter values for a Monte Carlo study |
|
|
MODEL COVERAGE-label: |
describes the group-specific population parameter values in multiple group analysis and the population parameter values for each categorical latent variable and combinations of categorical latent variables in mixture modeling for a Monte Carlo study |
|
|
MODEL COVERAGE: %OVERALL%
%class label% |
describes the overall population parameter values of a mixture model for a Monte Carlo study describes the class-specific population parameter values of a mixture model |
|
|
MODEL COVERAGE: %WITHIN%
%BETWEEN%
%BETWEEN label% |
describes the individual-level population parameter values for coverage describes the cluster-level population parameter values for a two-level model for coverage describes the cluster-level population parameter values for a three-level or cross-classified model for coverage |
|
|
MODEL MISSING: |
describes the missing data generation model for a Monte Carlo study |
|
|
MODEL MISSING-label: |
describes the group-specific missing data generation model for a Monte Carlo study |
|
|
MODEL MISSING: %OVERALL% %class label% |
describes the overall data generation model of a mixture model describes the class-specific data generation model of a mixture model |
|
The MODEL command is required for all analyses except exploratory factor analysis (EFA), exploratory latent class analysis (LCA), a baseline model, and TYPE=BASIC.
MODEL COMMAND OPTIONS
There are three major options in the MODEL command that are used to describe the relationships among observed variables and latent variables in the model. They are:
· BY
· ON
· WITH
BY is used to describe the regression relationships in the measurement model for the indicators of the continuous latent variables. These relationships define the continuous latent variables in the model. BY is short for measured by. ON is used to describe the regression relationships among the observed and latent variables in the model. It is short for regressed on. WITH is used to describe correlational (covariance) relationships in the measurement and structural models. It is short for correlated with.
The model in the following figure is used to illustrate the use of the BY, ON, and WITH options. The squares represent observed variables and the circles represent latent variables. Regression relationships are represented by arrows from independent variables to dependent variables. The variables f1 and f2 are continuous latent variables. The observed dependent variables are y1, y2, y3, y4, y5, y6, y7, y8, and y9. The measurement part of the model consists of the two continuous latent variables and their indicators. The continuous latent variable f1 is measured by y1, y2, y3, y4, and y5. The continuous latent variable f2 is measured by y6, y7, y8, and y9. The structural part of the model consists of the regression of the two continuous latent variables on nine observed independent variables. The observed independent variables are x1, x2, x3, x4, x5, x6, x7, x8, and x9. Following is the MODEL command for the figure below:
MODEL: f1 BY y1-y5;
f2 BY y6-y9;
f1 f2 ON x1-x9;
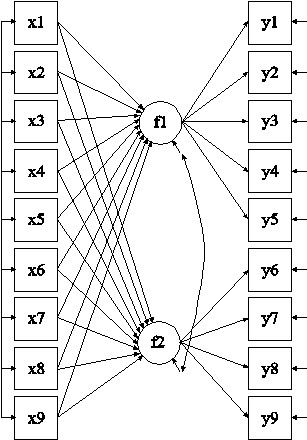
The BY option is used to name and define the continuous latent variables in the model. BY is short for measured by. The parameters that are estimated are sometimes referred to as factor loadings or lambdas. These are the coefficients for the regressions of the observed dependent variables on the continuous latent variables. These observed dependent variables are sometimes referred to as factor indicators. Each BY statement can be thought of as a set of ON statements that describes the regressions of a set of observed variables on a continuous latent variable or factor. However, continuous latent variables in the measurement model cannot be specified using a set of ON statements because BY statements are used to name the continuous latent variables. BY statements also provide a set of convenient defaults.
Observed factor indicators for continuous latent variables can be continuous, censored, binary, ordered categorical (ordinal), or counts. Factor indicators can also be continuous latent variables or the inflation part of censored and count variables. Combinations of all factor indicator types are allowed. With TYPE=TWOLEVEL and TYPE=TWOLEVEL MIXTURE, factor indicators for continuous latent variables can be between-level random effects. These factor indicators can appear only on the BETWEEN level.
CONFIRMATORY FACTOR ANALYSIS MODELING
In this section the use of the BY option for confirmatory factor analysis (CFA) models is described. Following are the two BY statements that describe how the continuous latent variables in the figure above are measured:
f1 BY y1- y5;
f2 BY y6- y9;
The factor loading of any observed variable mentioned on the right-hand side of the BY statement is free to be estimated with the exception of the factor loading of the first variable after the BY option. This factor loading is fixed at one as the default. Fixing a factor loading of an indicator of a continuous latent variable sets the metric of the continuous latent variable. Setting the metric can also be accomplished by fixing the variance of the continuous latent variable to one and freeing the factor loading of the factor indicator that is fixed at one as the default. In the example above, the factor loadings of y1 and y6 are fixed at one. The other factor loadings are estimated using default starting values of one.
Following is an example of how to set the metric of the continuous latent variable by fixing the variance of the continuous latent variable to one and allowing all factor loadings to be free:
f1 BY y1* y2- y5;
f2 BY y6* y7- y9;
f1@1 f2@1;
where the asterisk (*) after y1 and y6 frees the factor loadings of y1 and y6, and the @1 after f1 and f2 fixes the variances of f1 and f2 to one. The use of the asterisk (*); @ symbol; and the specification of means, thresholds, variances, and covariances are discussed later in the chapter.
Residual variances are estimated as the default when factor indicators are continuous or censored. Residual covariances among the factor indicators are fixed at zero as the default. All default settings can be overridden. How to do so is discussed later in this chapter.
The BY option can also be used to define continuous latent variables underlying other continuous latent variables that have observed factor indicators. This is referred to as second-order factor analysis. However, a continuous latent variable cannot be used on the right-hand side of a BY statement before it has been defined on the left-hand side of another BY statement. For example, the following statements are acceptable:
f1 BY y1 y2 y3 y4 y5;
f2 BY y6 y7 y8 y9;
f3 BY f1 f2;
whereas, the following statements are not acceptable:
f3 BY f1 f2;
f1 BY y1 y2 y3 y4 y5;
f2 BY y6 y7 y8 y9;
because f1 and f2 are used on the right-hand side of a BY statement before they are defined on the left-hand side of a BY statement.
EXPLORATORY STRUCTURAL EQUATION MODELING
In this section the use of the BY option for exploratory structural equation (ESEM) modeling (Asparouhov & Muthén, 2009a) is described. One of the differences between CFA and EFA factors is that CFA factors are not rotated. For a set of EFA factors, the factor loading matrix is rotated as in conventional EFA using the rotations available through the ROTATION option of the ANALYSIS command. A set of EFA factors must have the same factor indicators. A set of EFA factors can be regressed on the same set of covariates. An observed or latent variable can be regressed on a set of EFA factors. EFA factors are allowed with TYPE=GENERAL and TYPE=COMPLEX with observed dependent variables that are continuous, censored, binary, ordered categorical (ordinal), and combinations of these variable types. EFA factors are not allowed when summary data are analyzed or when the MLM, MLMV, or GLS estimators are used.
The BY option has three special features that are used with sets of EFA factors in the MODEL command. One feature is used to define sets of EFA factors. The second feature is a special way of specifying factor loading matrix equality for sets of EFA factors. The third feature is used in conjunction with the TARGET setting of the ROTATION option of the ANALYSIS command to provide target factor loading values to guide the rotation of the factor loading matrix for sets of EFA factors.
DEFINING EFA FACTORS
Following is an example of how to define a set of EFA factors using the BY option:
f1-f2 BY y1-y5 (*1);
where the asterisk (*) followed by a label specifies that factors f1 and f2 are a set of EFA factors with factor indicators y1 through y5.
Following is an alternative specification:
f1 BY y1-y5 (*1);
f2 BY y1-y5 (*1);
where the label 1 specifies that factors f1 and f2 are part of the same set of EFA factors. Rotation is carried out on the five by two factor loading matrix. Labels for EFA factors must follow an asterisk (*). EFA factors with the same label must have the same factor indicators.
More than one set of EFA factors may appear in the MODEL command. For example,
f1-f2 BY y1-y5 (*1);
f3-f4 BY y6-y10 (*2);
specifies that factors f1 and f2 are one set of EFA factors with the label 1 and factors f3 and f4 are another set of EFA factors with the label 2. The two sets of EFA factors are rotated separately.
Factors in a set of EFA factors can be regressed on covariates but the set of covariates must be the same, for example,
f1-f2 ON x1-x3;
or
f1 ON x1-x3;
f2 ON x1-x3;
A set of EFA factors can also be used as covariates in a regression, for example,
y ON f1-f2;
EQUALITIES WITH EFA FACTORS
The BY option has a special convention for specifying equalities of the factor loading matrices for more than one set of EFA factors. The equality label is placed after the label that defines the set of EFA factors and applies to the entire factor loading matrix not to a single parameter. Following is an example of how to specify that the factor loading matrices for the set of EFA factors f1 and f2 and the set of EFA factors f3 and f4 are held equal:
f1-f2 BY y1-y5 (*1 1);
f3-f4 BY y6-y10 (*2 1);
The number 1 following the labels 1 and 2 that define the EFA factors specifies that the factor loadings matrices for the two sets of EFA factors are held equal.
TARGET ROTATION WITH EFA FACTORS
The BY option has a special feature that is used with the TARGET setting of the ROTATION option of the ANALYSIS command to specify target factor loading values for a set of EFA factors (Browne, 2001). The target factor loading values are used to guide the rotation of the factor loading matrix. Typically these values are zero. For the TARGET rotation, a minimum number of target values must be given for purposes of model identification. For the default oblique TARGET rotation, the minimum is m(m-1) where the m is the number of factors. For the orthogonal TARGET rotation, the minimum is m(m-1)/2. The target values are given in the MODEL command using the tilde (~) symbol. The target values are specified in a BY statement using the tilde (~) symbol as follows:
f1 BY y1-y5 y1~0 (*1);
f2 BY y1-y5 y5~0 (*1);
where the target factor loading values for the factor indicator y1 for factor f1 and y5 for factor f2 are zero.
The ON option is used to describe the regression relationships in the model and is short for regressed on. The general form of the ON statement is:
y ON x;
where y is a dependent variable and x is an independent variable. Dependent and independent variables can be observed or latent variables.
In the previous figure, the structural relationships are the regressions of the continuous latent variables f1 and f2 on the nine independent variables x1 through x9. The ON statements shown below are used to specify these regressions:
f1 ON x1-x9;
f2 ON x1-x9;
These statements specify that regression coefficients are free to be estimated for f1 and f2 regressed on the independent variables x1 through x9 with default starting values of zero.
For continuous latent variables, the residual variances are estimated as the default. The residuals of the latent variables are correlated as the default because residuals are correlated for latent variables that do not influence any other variable in the model except their own indicators. These defaults can be overridden. Means, variances, and covariances of the independent variables in the model should not be mentioned in the MODEL command because the model is estimated conditioned on the covariates.
An ON statement can be used to describe the regression relationship between an observed dependent variable and an observed independent variable. Following is an example of how to specify the regression of an observed dependent variable y9 on the observed independent variable x9:
y9 ON x9;
The general form of the ON statement is used to describe regression relationships for continuous latent variables and observed variables that are continuous, censored, binary, ordered categorical (ordinal), counts, censored inflated, and count inflated. The ON option has special features for categorical latent variables and unordered categorical (nominal) observed variables which are described below.
CATEGORICAL LATENT VARIABLES AND UNORDERED CATEGORICAL (NOMINAL) OBSERVED VARIABLES
For categorical latent variables and unordered categorical (nominal) observed variables, the ON option is used to describe the multinomial logistic regression of the categorical latent variable or the unordered categorical (nominal) observed variable on one or more independent variables.
For a categorical latent variable, an ON statement is specified for each latent class except the last class which is the reference class. A class label is used to refer to each class. Class labels use the convention of adding to a variable name the number symbol (#) followed by a number. For a categorical latent variable c with three classes,
c#1 c#2 ON x1-x3;
specifies that regression coefficients are free to be estimated for classes 1 and 2 of the categorical latent variable c regressed on the independent variables x1, x2, and x3. The intercepts in the regression of the categorical latent variable on the independent variables are free to be estimated as the default.
The statement above can be simplified to the following:
c ON x1-x3;
The multinomial logistic regression of one categorical latent variable on another categorical latent variable where c2 has four classes and c1 has three classes is specified as follows:
c2 ON c1;
or
c2#1 c2#2 c2#3 ON c1#1 c1#2;
For an unordered categorical (nominal) observed variable, an ON statement is specified for each category except the last category which is the reference category. A category label is used to refer to each category. Category labels use the convention of adding to a variable name the number symbol (#) followed by a number. For a three-category variable u,
u#1 u#2 ON x1-x3;
specifies that regression coefficients are free to be estimated for categories 1 and 2 of the unordered categorical (nominal) observed variable u regressed on the independent variables x1, x2, and x3. The thresholds in the regression of the unordered categorical (nominal) observed variable on the independent variables are free to be estimated as the default.
The statement above can be simplified to the following:
u ON x1-x3;
Following is a table that describes how the relationships between dependent variables and observed mediating variables or latent variables are specified. Relationships with the designation of NA are not allowed. Relationships not specified using the ON option are specified by listing for each class the intercepts or thresholds in square brackets and the residual variances with no brackets. Not shown in the table is that all dependent variables can be regressed on independent variables that are not mediating variables using the ON option.
|
Scale of Dependent Variable |
Scale of Observed Mediating Variable |
Scale of Latent Variable |
||||
|
Continuous |
Censored, Categorical, and Count |
Nominal |
Continuous |
Categorical |
Inflation Part of Censored and Count |
|
|
Continuous |
ON |
ON |
NA |
ON |
Mean and variance vary across classes |
NA |
|
Censored, Categorical, and Count |
ON |
ON |
NA |
ON |
Mean/ threshold and variance vary across classes |
NA |
|
Nominal |
ON |
ON |
NA |
ON |
Means vary across classes |
NA |
|
Continuous Latent |
ON |
ON |
NA |
ON |
Mean and variance vary across classes |
NA |
|
Categorical Latent |
ON |
ON |
NA |
ON |
ON |
NA |
|
Inflation Part of Censored and Count |
ON |
ON |
NA |
ON |
Mean varies across classes |
NA |
A second form of the ON option is PON. PON is used to describe the paired regression relationships in the model and is short for regressed on. PON pairs the variables on the left-hand side of the PON statement with the variables on the right-hand side of the PON statement. For PON, the number of variables on the left-hand side of the PON statement must equal the number of variables on the right-hand side of the PON statement. For example,
y2 y3 y4 PON y1 y2 y3;
implies
y2 ON y1;
y3 ON y2;
y4 ON y3;
The PON option cannot be used with the simplified language for categorical latent variables or unordered categorical (nominal) observed variables.
The WITH option is used to describe correlational relationships in a model and is short for correlated with. Correlational relationships include covariances among continuous observed variables and continuous latent variables and among categorical latent variables. With the weighted least squares estimator, correlational relationships are also allowed for binary, ordered categorical, and censored observed variables. For all other variable types, the WITH option cannot be used to specify correlational relationships. Special modeling needs to be used in these situations, for example, using a latent variable that influences both variables.
The NOCOVARIANCES setting of the MODEL option of the ANALYSIS command specifies that the covariances and residual covariances among all latent and observed variables in the analysis model are fixed at zero. The WITH option is used to free selected covariances and residual covariances.
Following is an example of how to specify the WITH option:
f1 WITH f2;
This statement frees the covariance parameter for the continuous latent variables f1 and f2.
Several variables can be included on both sides of the WITH statement. In this situation, the variables on the left-hand side of the WITH statement are crossed with the variables on the right-hand side of the WITH statement resulting in all possible combinations of left- and right-hand side variables.
The association between two categorical latent variables c1 and c2 where c1 has three classes and c2 has four classes is specified as follows:
c1#1 c1#2 WITH c2#1 c2#2 c2#3;
The statement above can be simplified to:
c1 WITH c2;
The association coefficient for the last class of each categorical latent variable is fixed at zero as the default as in loglinear modeling.
A second form of the WITH option is PWITH. PWITH pairs the variables on the left-hand side of the PWITH statement with those on the right-hand side of the PWITH statement. For PWITH, the number of variables on the left-hand side of the PWITH statement must equal the number of variables on the right-hand side of the PWITH statement. For example,
y1 y2 y3 PWITH y4 y5 y6;
implies
y1 WITH y4;
y2 WITH y5;
y3 WITH y6;
whereas,
y1 y2 y3 WITH y4 y5 y6;
implies
y1 WITH y4;
y1 WITH y5;
y1 WITH y6;
y2 WITH y4;
y2 WITH y5;
y2 WITH y6;
y3 WITH y4;
y3 WITH y5;
y3 WITH y6;
The PWITH option cannot be used with the simplified language for categorical latent variables.
For convenience, no distinction is made in how variances and residual variances are referred to in the MODEL command. The model defines whether the parameter to be estimated is a variance or a residual variance. Variances are estimated for independent variables and residual variances are estimated for dependent variables. Variances of continuous and censored observed variables and continuous latent variables are free to be estimated as the default. Variances of categorical observed variables are not estimated. When the Theta parameterization is used in either a growth model or a multiple group model, variances for continuous latent response variables for the categorical observed variables are estimated. Unordered categorical (nominal) observed variables, observed count variables, and categorical latent variables have no variance parameters.
A list of observed or latent variables refers to the variances or residual variances of those variables. For example,
y1 y2 y3;
refers to the variances of y1, y2, and y3 if they are independent variables and refers to the residual variances of y1, y2, and y3 if they are dependent variables. The statement means that the variances or residual variances are free parameters to be estimated using default starting values.
Means, intercepts, and thresholds are included in the analysis model as the default. The NOMEANSTRUCTURE setting of the MODEL option of the ANALYSIS command is used with TYPE=GENERAL to specify that means, intercepts, and thresholds are not included in the analysis model.
For convenience, no distinction is made in how means and intercepts are referred to in the MODEL command. The model defines whether the parameter to be estimated is a mean or an intercept. Means are estimated for independent observed variables and observed variables that are neither independent nor dependent variables in the model. Means for nominal variables are logit coefficients corresponding to probabilities for each category except the last category. Means for count variables are log rates. Means for time-to-event variables in continuous-time survival analysis are log rates. Means are also estimated for independent continuous latent variables and independent categorical latent variables. For an independent categorical latent variable, the means are logit coefficients corresponding to probabilities for each class except the last class.
Intercepts are estimated for continuous observed dependent variables, censored observed dependent variables, unordered categorical (nominal) observed dependent variable, count observed dependent variables, baseline hazard parameters for continuous-time survival analysis, continuous latent dependent variables, and categorical latent dependent variables.
Thresholds are estimated for binary and ordered categorical observed variables. The sign of a threshold is the opposite of the sign of a mean or intercept for the same variable. For example, with a binary dependent variable, a threshold of -0.5 is the same as an intercept of .5.
A list of observed or latent variables enclosed in brackets refers to means, intercepts, or thresholds.
For example,
[y1 y2 y3];
refers to the means of variables y1, y2, and y3 if they are independent variables and refers to the intercepts if they are continuous dependent variables. This statement indicates that the means or intercepts are free parameters to be estimated using the default starting values.
If the variables are categorical, the thresholds are referred to as follows,
[y1$1 y1$2 y1$3 y2$1 y2$2];
where y1 is a four category variable with three thresholds and y2 is a three category variable with two thresholds. y1$1 refers to the first and lowest threshold of variable y1; y1$2 refers to the next threshold; and y1$3 refers to the highest threshold. This statement means that the thresholds are free parameters to be estimated using the default starting values.
For models with a mean structure, all means, intercepts, and thresholds of observed variables are free to be estimated at the default starting values. The means and intercepts of continuous latent variables are fixed at zero in a single group analysis. In a multiple group analysis, the means and intercepts of the continuous latent variables are fixed at zero in the first group and are free to be estimated in the other groups. In a mixture model, the means and intercepts of the continuous latent variables are fixed at zero in the last class and are free to be estimated in the other classes. The means and intercepts of categorical latent variables are fixed at zero in the last class and are free to be estimated in the other classes.
CONVENIENCE FEATURES FOR THE MODEL COMMAND
There are several features that make it easier for users to specify the model to be estimated. One feature is the list function. A user can use a hyphen to specify a list of variables, a list of equality constraints, and a list of parameter labels.
When using the list function, it is important to know the order of observed and latent variables that the program expects. The order of observed variables is determined by the order of variables in the NAMES or USEVARIABLES options of the VARIABLE command. If all of the variables in NAMES statement are used in the analysis, then the order is taken from there. If the variables for the analysis are a subset of the variables in the NAMES statement, the order is taken from the USEVARIABLES statement.
The order of continuous latent variables is determined by the order of the BY and | statements in the MODEL command. Factors defined using the BY option come first in the order that they occur in the MODEL command followed by the random effects defined using the | symbol in the order that they occur in the MODEL command.
The list function can be used on the left- and right-hand sides of ON and WITH statements and on the right-hand side of BY statements. A list on the left-hand side implies multiple statements. A list on the right-hand side implies a list of variables.
Following is an example of the use of the list function on the right-hand side of a BY statement. It assumes the variables are in the order: y1, y2, y3, y4, y5, y6, y7, y8, y9, y10, y11, and y12.
f1 BY y1-y4;
f2 BY y5-y9;
f3 BY y10-y12;
The program would interpret these BY statements as:
f1 BY y1 y2 y3 y4;
f2 BY y5 y6 y7 y8 y9;
f3 BY y10 y11 y12;
To use the list function with latent variables the order of latent variables would be f1, f2, f3 because of the order of the BY statements in the MODEL command.
Following is an example of using the list function on both the left- and the right-hand sides of the ON statement:
f1-f3 ON x1-x3;
This implies the multiple statements:
f1 ON x1 x2 x3;
f2 ON x1 x2 x3;
f3 ON x1 x2 x3;
The list function can also be used with the WITH option,
y1-y3 WITH y4-y6;
This implies
y1 WITH y4;
y1 WITH y5;
y1 WITH y6;
y2 WITH y4;
y2 WITH y5;
y2 WITH y6;
y3 WITH y4;
y3 WITH y5;
y3 WITH y6;
FREEING PARAMETERS AND ASSIGNING STARTING VALUES
The asterisk (*) is used to free a parameter and/or assign a starting value for the estimation of that parameter. It is placed after a parameter with a number following it. For example:
y1*.5;
is interpreted as freeing the variance/residual variance of y1 to be estimated with a starting value of 0.5.
Consider the BY statements from the previous section:
f1 BY y1 y2 y3 y4 y5;
f2 BY y6 y7 y8 y9;
As mentioned previously, the above statements result in the factor loadings for y1 and y6 being fixed at one in order to set the metric of the latent variables f1 and f2. All of the other parameters mentioned are free to be estimated with starting values of one. Consider the following BY statements:
f1 BY y1* y2*0.5 y3 y4 y5;
f2 BY y6 y7-y9*0.9;
By putting an asterisk (*) after y1, the y1 parameter is freed at the default starting value of one instead of being fixed at one by default. By placing an asterisk (*) followed by 0.5 behind y2, the parameter starting value is changed from the default starting value of 1 to 0.5. The variables y3, y4, and y5 are free to be estimated at the default starting value of one. In the BY statement for f2 the variables y7, y8, and y9 are specified using the list function, y7-y9, followed by an asterisk (*) and the value 0.9. This changes the starting values for y7, y8, and y9 from the default starting value of 1 to 0.9.
These same features can be used with the ON and WITH options and for assigning starting values to variances, means, thresholds, and scales.
Following are examples of assigning starting values to a variety of parameters:
f1 ON x1-x3*1.5;
f1 WITH f2*.8;
y1-y12*.75;
[f1-f3*.5];
{y1-y12*5.0};
In some cases, it is necessary to fix a parameter at a specific value. The @ symbol is used to fix the values of parameters. Consider the following example based on the measurement model in the earlier figure. Following are the specifications needed to free the value of the first indicator of each latent variable at starting values of one and to fix the value of the second indicator of each latent variable to one in order to set the metric of each latent variable:
f1 BY y1* y2@1 y3 y4 y5;
f2 BY y6* y7@1 y8 y9;
By placing an asterisk (*) after y1, the factor loading for y1 is estimated using the starting value of one. By placing @1 after y2, the factor loading for y2 is fixed at one. Likewise, by placing an asterisk (*) after y6, the factor loading for y6 is estimated using the starting value of one. By placing @1 after y7, the factor loading for y7 is fixed at one.
The @ symbol can be used to fix any parameter in a model. The following example fixes the covariance between f1 and f2 at zero:
f1 WITH f2@0;
CONSTRAINING PARAMETER VALUES TO BE EQUAL
Parameters can be constrained to be equal by placing the same number in parentheses following the parameters that are to be held equal. This convention can be used for all parameters. Following is an example in which regression coefficients, residual variances, and residual covariances are held equal:
y1 ON x1 (1) ;
y2 ON x2 (1) ;
y3 ON x3 (1) ;
y1 y2 y3 (2);
y1 WITH y2-y3 (3);
In the above example, the regression coefficients for the three regressions are constrained to be equal, the three residual variances are constrained to be equal, and the two residual covariances are constrained to be equal.
There can be only one number in parentheses on each line. If a statement continues on more than one line, the number in parentheses must be stated at the end of each line.
For example,
f1 BY y1 y2 y3 y4 y5 y6 y7 y8 y9 y10 y11 y12 (1)
y13 y14 y15 (1);
specifies that the factor loadings of y2 through y15 are constrained to be equal. The factor loading of y1 is fixed at one as the default.
The following statement,
f1 BY y1 y2 y3 y4 y5 y6 y7 y8 y9 y10 y11 y12
y13 y14 y15 (1);
specifies that the factor loadings of y13, y14, and y15 are constrained to be equal because (1) refers to only the information on the line on which it is located.
The following statement,
f1 BY y1 y2 y3 y4 y5 (1)
y6 y7 y8 y9 y10 (2)
y11 y12 y13 y14 y15 (3);
specifies that the factor loading of y1 is fixed at one and that the factor loadings of y2, y3, y4, and y5 are held equal, that the factor loadings of y6, y7, y8, y9, and y10 are held equal, and that the factor loadings of y11, y12, y13, y14, and y15 are held equal.
Following are examples of how to constrain the parameters of means, intercepts and/or thresholds to be equal.
[y1 y2 y3] (1);
indicates that the means/intercepts of variables y1, y2, and y3 are constrained to be equal. The statements
[u1$1 u2$1 u3$1] (2);
[u1$2 u2$2 u3$2] (3);
[u1$3 u2$3 u3$3] (4);
indicate that the first threshold for variables u1, u2, and u3 are constrained to be equal; that the second threshold for variables u1, u2, and u3 are constrained to be equal; and that the third threshold for variables u1, u2, and u3 are constrained to be equal. Out of nine possible thresholds, three parameters are estimated. Only one set of parentheses can be included on each line of the input file.
USING THE LIST FUNCTION FOR ASSIGNING STARTING VALUES, FIXING VALUES, CONSTRAINING VALUES TO BE EQUAL, AND ASSIGNING LABELS TO PARAMETERS
The list function is convenient for assigning starting values to parameters, fixing parameters values, constraining parameter values to be equal, and assigning labels to parameters.
ASSIGNING STARTING VALUES TO PARAMETERS
Following is an example of how to use the list function to assign starting values to parameters:
f1 BY y1 y2-y4*0;
f2 BY y5 y6-y9*.5;
f3 BY y10 y11-y12*.75;
The program interprets these BY statements as:
f1 BY y1 y2*0 y3*0 y4*0;
f2 BY y5 y6*.5 y7*.5 y8*.5 y9*.5;
f3 BY y10 y11*.75 y12*.75;
where the starting value of 0 is assigned to the factor loadings for y2, y3, and y4; the starting value of .5 is assigned to the factor loadings for y6, y7, y8, and y9; and the starting value of .75 is assigned to the factor loadings for y11 and y12. The factor loading for the first factor indicator of each factor is fixed at one as the default to set the metric of the factor.
FIXING PARAMETER VALUES
Following is an example of using the list function to fix parameter values:
f1-f3@1;
The statement above fixes the variances/residual variances of f1, f2, and f3 at one.
CONSTRAINING PARAMETER VALUES TO BE EQUAL
Following is an example of using the list function to constrain parameter values to be equal:
f1 BY y1-y5 (1)
y6-y10 (2);
The statement above specifies that the factor loadings of y2, y3, y4, and y5 are held equal and that the factor loadings of y6, y7, y8, y9, and y10 are held equal. The factor loading of y1 is fixed at one as the default to set the metric of the factor.
The list function can be used to assign equalities to a list of parameters using a list of equality constraints. A list of equality constraints cannot be used with a set of individual parameters. Following is an example of how to use the list function with a list of parameters on the right-hand side of the BY option:
f1 BY y1
y2-y5 (2-5);
f2 BY y6
y7-y10 (2-5);
The statements above specify that the factor loadings for y2 and y7 are held equal, the factor loadings for y3 and y8 are held equal, the factor loadings for y4 and y9 are held equal, and the factor loadings for y5 and y10 are held equal. This can also be specified as shown below for convenience.
f1 BY y1-y5 (1-5);
f2 BY y6-y10 (1-5);
No equality constraint is assigned to y1 and y6 even though they are part of the list of variables because they are fixed at one to set the metric of the factors. The number of equalities in the list must equal the number of variables on the right-hand side of the BY option.
A list of equality constraints cannot be used with a list of parameters on the left-hand side of an option. Following is an example of how equality constraints are specified for a list of parameters on the left-hand side of the ON option:
y1-y3 ON x (1 2 3);
y4-y6 ON x (1 2 3);
where the regression coefficients in the regression of y1 on x and y4 on x are constrained to be equal; the regression coefficients in the regression of y2 on x and y5 on x are constrained to be equal; and the regression coefficients in the regression of y3 on x and y6 on x are constrained to be equal.
Following is an example of how equalities are specified when a list of parameters appears on both the left- and right-hand sides of an option:
y1-y3 ON x1-x2 (1-2 3-4 5-6);
y4-y6 ON x1-x2 (1-2 3-4 5-6);
Each variable on the left-hand side of the ON option must have a list of equalities for use with the variables on the right-hand side of the ON option. Because there are three variables on the left-hand side of the ON statement and two variables on the right-hand side of the ON statement, three lists of two equalities are needed. A single list cannot be used.
Following is what this specifies:
y1 ON x1 (1);
y1 ON x2 (2);
y2 ON x1 (3);
y2 ON x2 (4);
y3 ON x1 (5);
y3 ON x2 (6);
y4 ON x1 (1);
y4 ON x2 (2);
y5 ON x1 (3);
y5 ON x2 (4);
y6 ON x1 (5);
y6 ON x2 (6);
The list function can be used with the simplified language for categorical latent variables and unordered categorical (nominal) observed variables. The multinomial logistic regression of one categorical latent variable on another categorical latent variable where c2 has four classes and c1 has three classes is specified as follows:
c2 ON c1;
Following is an example of how equalities are specified when a list of parameters appears on both the left- and right-hand sides of the ON option using the simplified language:
c2 ON c1 (1-2 1-2 1-2);
or
c2 ON c1 (1-2);
Following is what this specifies:
c2#1 ON c1#1 (1);
c2#2 ON c1#2 (2);
c2#3 ON c1#1 (1);
c2#1 ON c1#2 (2);
c2#2 ON c1#1 (1);
c2#3 ON c1#3 (2);
ASSIGNING LABELS TO PARAMETERS
The list function can be used to assign labels to parameters in the MODEL command. Following is an example of how to use the list function in this way:
[y1-y5] (p1-p5);
The statement above assigns the parameter label p1 to y1, p2 to y2, p3 to y3, p4 to y4, and p5 to y5.
The list function can be used to assign labels to a list of parameters using a list of labels. A list of labels cannot be used with a set of individual parameters. Following is an example of how to use the list function with a list of parameters on the right-hand side of the BY option:
f1 BY y1
y2-y5 (p2-p5);
The statement above assigns the label p2 to the factor loading for y2, p3 to the factor loading for y3, p4 to the factor loading for y4, and p5 to the factor loading for y5.
A list of labels cannot be used with a list of parameters on the left-hand side of an option. Following is an example of how labels are specified for a list of parameters on the left-hand side of the ON option:
y1-y3 ON x (p1 p2 p3);
where the regression coefficient in the regression of y1 on x is assigned the label p1; the regression coefficient in the regression of y2 on x is assigned the label p; and the regression coefficient in the regression of y3 on x is assigned the label p3.
Following is an example of how labels are specified when a list of parameters appears on both the left- and right-hand sides of an option:
y1-y3 ON x1-x2 (p1-p2 p3-p4 p5-p6);
Each variable on the left-hand side of the ON option must have a list of labels for use with the variables on the right-hand side of the ON option. Because there are three variables on the left-hand side of the ON statement and two variables on the right-hand side of the ON statement, three lists of two equalities are needed. A single list cannot be used.
Because there are three variables on the left-hand side of the ON statement and two variables on the right-hand side of the ON statement, three lists of two equalities are needed.
Following is what this specifies:
y1 ON x1 (p1);
y1 ON x2 (p2);
y2 ON x1 (p3);
y2 ON x2 (p4);
y3 ON x1 (p5);
y3 ON x2 (p6);
The list function can be used with the simplified language for categorical latent variables and unordered categorical (nominal) observed variables.
The multinomial logistic regression of one categorical latent variable on another categorical latent variable where c2 has four classes and c1 has three classes is specified as follows:
c2 ON c1;
Following is an example of how labels are assigned when a list of parameters appears on both the left- and right-hand sides of the ON option using the simplified language:
c2 ON c1 (p1-p2 p3-p4 p5-p6);
Following is what this specifies:
c2#1 ON c1#1 (p1);
c2#2 ON c1#2 (p2);
c2#3 ON c1#1 (p3);
c2#1 ON c1#2 (p4);
c2#2 ON c1#1 (p5);
c2#3 ON c1#3 (p6);
SPECIAL LIST FUNCTION FEATURE
The list function has a special feature that can make model specification easier. This feature allows a parameter to be mentioned in the MODEL command more than once. The last specification is used in the analysis. For example,
f1 BY y1-y6*0 y5*.5;
is interpreted by the program as
f1 BY y1*0 y2*0 y3*0 y4*0 y5*.5 y6*0;
Although y5 is assigned a starting value of 0.0 in the beginning of the BY statement using the list function, y5 is assigned a starting value of 0.5 later in the statement. The program uses the last specification.
If a variable is mentioned more than once on the right-hand side of a BY, ON, or WITH statement or in a list of variances, means, or scale factors, the program uses the last value it reads. This makes it convenient when a user wants all of the starting values in a list to be the same except for a few. The same feature can be used when fixing values. For example,
f1-f4@1 f3@2;
fixes the variances/residual variances of f1, f2, and f4 at one and fixes the variance/residual variance of f3 at 2.
This feature can also be used with equalities, however, the variable from the list that is not to be constrained to be equal must appear on a separate line in the input file. In a line with an equality constraint, anything after the equality constraint is ignored. For example,
f1 BY y1-y5 (1)
y4
y6-y10 (2);
indicates that the factor loadings for y2, y3, and y5 are held equal, the factor loading for y4 is free and not equal to any other factor loading, and the factor loadings for y6, y7, y8, y9, and y10 are held equal. The factor loading for y1 is fixed at one as the default.
For binary and ordered categorical dependent variables, thresholds are referred to by using the convention of adding to a variable name a dollar sign ($) followed by a number. The number of thresholds is equal to the number of categories minus one. For example, if u1 is an ordered categorical variable with four categories it has three thresholds. These thresholds are referred to as u1$1, u1$2, and u1$3.
LABELING CATEGORICAL LATENT VARIABLES AND UNORDERED CATEGORIAL (NOMINAL) OBSERVED VARIABLES
The classes of categorical latent variables and the categories of unordered categorical (nominal) observed variables are referred to by using the convention of adding to a variable name a number sign (#) followed by the category/class number. For example, if c is a categorical latent variable with three classes, the first two classes are referred to as c#1 and c#2. The third class has all parameters fixed at zero as a reference category. If u1 is a nominal variable with three categories, the first two categories are referred to as u1#1 and u1#2. The third category has all parameters fixed at zero as a reference category. With the ON option categorical latent variables and unordered categorical (nominal) observed variables can be referred to by their variable name. With the WITH option, categorical latent variables can be referred to by their variable name.
Censored and count inflation variables are referred to by using the convention of adding to a variable name a number sign (#) followed by the number one. For example, if y1 is a censored variable, the inflation part of y1 is referred to as y1#1. If u1 is a count variable, the inflation part of u1 is referred to as u1#1.
LABELING BASELINE HAZARD PARAMETERS
In continuous-time survival modeling, there are as many baseline hazard parameters are there are time intervals plus one. When the BASEHAZARD option of the ANALYSIS command is ON, these parameters can be referred to by using the convention of adding to the name of the time-to-event variable the number sign (#) followed by a number. For example, for a time-to-event variable t with 5 time intervals, the six baseline hazard parameters are referred to as t#1, t#2, t#3, t#4, t#5, and t#6.
LABELING CLASSES OF A CATEGORICAL LATENT VARIABLE
In the MODEL command, categorical latent variable classes are referred to using labels. These labels are constructed by using the convention of adding to the name of the categorical latent variable a number sign (#) followed by a number. For example, if c is a categorical latent variable with four classes, the labels for the four classes are c#1, c#2, and c#3. The last class is the reference class.
Labels can be assigned to parameters by placing a name in parentheses following the parameter in the MODEL command. These labels are used in three ways. First, they are used in conjunction with the MODEL CONSTRAINT command to define linear and non-linear constraints on the parameters in the model. Second, they are used with the MODEL TEST command to test linear restrictions on the model defined in the MODEL and MODEL CONSTRAINT commands. Third, they are used with ESTIMATOR=BAYES and the MODEL PRIORS command to specify the prior distribution for parameters in the MODEL command.
The parameter labels follow the same rules as variable names. They can be up to 8 characters in length; must begin with a letter; can contain only letters, numbers, and the underscore symbol; and are not case sensitive. Only one label can appear on a line. Following is an example of how to label parameters:
MODEL: y ON x1 (p1)
x2 (p2)
x3 (p3);
where p1 is the label assigned to the regression slope for y on x1, p2 is the label assigned to the regression slope for y on the x2, and p3 is the label assigned to the regression slope for y on x3.
The list function can be used to assign labels. Following is an example of how to use the list function to label parameters:
MODEL: [y1-y10] (q1-q10);
y1-y10 (p1-p10);
f BY y1-y10 (z2-z10);
where the labels q1 through q10 are assigned to the intercepts of y1 through y10, the labels p1 through p10 are assigned to the residual variances of y1 through y10, and the labels z2 through z10 are assigned to the factors loadings for y2 through y10. The factor loading of y1 is fixed at one as the default to set the metric of the factor.
If a list of labels is used, for example, in MODEL PRIORS, the order of the labels is alphabetical not the order of the labels in the MODEL command. For example, the list p4-q2 includes p4, p5, p6, p7, p8, p9, p10, q1, and q2.
The list function can be used with the ON and WITH options when there are lists of variable names on both the right- and left-hand sides of these options. Following is an example of how to use the list function to assign labels when there are lists of variables on both the right- and left-hand sides of ON:
y1-y3 ON x1-x2 (p1-p6);
The first variable on the left-hand side of ON is paired with all variables on the right-hand side. Then the second variable on the left-hand side of ON is paired with all variables on the right-hand side etc. The label p1 is assigned to the regression slope for y1 on x1. The label p2 is assigned to the regression slope for y1 on x2. The label p3 is assigned to the regression slope for y2 on y1. The label p6 is assigned to the regression slope for y3 on x2.
Following is an example of how to use the list function to assign labels when there are lists of variables on both the right- and left-hand sides of WITH:
y1-y3 WITH y1-y3 ( p1-p3);
The labels are assigned to the upper triangle of a symmetric matrix read row-wise. The label p1 is assigned to the covariance between y1 and y2. The label p2 is assigned to the covariance between y1 and y3. The label p3 is assigned to the covariance between y2 and y3.
In models that use TYPE=GENERAL, it may be useful to multiply each observed variable or latent response variable by a scale factor that can be estimated. For example, with categorical observed variables, a scale factor refers to the underlying latent response variables and facilitates growth modeling and multiple group analysis because the latent response variables are not restricted to have across-time or across-group equalities of variances. With continuous observed variables, using scale factors containing standard deviations makes it possible to analyze a sample covariance matrix by a correlation structure model.
A list of observed variables in curly brackets refers to scale factors. For example,
{u1 u2 u3};
refers to scale factors for variables u1, u2, and u3. This statement means that the scale factors are free parameters to be estimated using the default starting values of one.
The | symbol is used to specify growth models, to name and define random effect variables in the model, and to name and define latent variable interactions.
Following is a description of the language specific to growth models. The | symbol can be used with all analysis types to specify growth models. The names on the left-hand side of the | symbol name the random effect variables, also referred to as growth factors. The statement on the right-hand side of the | symbol names the outcome and specifies the time scores for the growth model.
Following is an example of the MODEL command for a quadratic growth model for a continuous outcome specified without using the | symbol:
MODEL: i BY y1-y4@1;
s BY y1@0 y2@1 y3@2 y4@3;
q BY y1@0 y2@1 y3@4 y4@9;
[y1-y4@0 i s q];
If the | symbol is used to specify the same growth model for a continuous outcome, the MODEL command is:
MODEL: i s q | y1@0 y2@1 y3@2 y4@3;
All of the other specifications shown above are done as the default. The defaults can be overridden by mentioning the parameters in the MODEL command after the | statement. For example,
MODEL: i s q | y1@0 y2@1 y3@2 y4@3;
[y1-y4] (1);
[i@0 s q];
changes the parameterization of the growth model from one with the intercepts of the outcome variable fixed at zero and the growth factor means free to be estimated to a parameterization with the intercepts of the outcome variable held equal, the intercept growth factor mean fixed at zero, and the slope growth factor means free to be estimated.
Many other types of growth models can be specified using the | symbol. Following is a table that shows how to specify some of these growth models using the | symbol and also how to specify the same growth models using the BY option and other options. All examples are for continuous outcomes unless specified otherwise.
|
|
Growth Language |
Alternative |
|
Intercept only |
MODEL: i | y1-y4@1; |
MODEL: i BY y1-y4@1; [y1-y4@0 i]; |
|
Linear |
MODEL: i s | y1@0 y2@1 y3@2 y4@3;
|
MODEL: i BY y1-y4@1; s BY y1@0 y2@1 y3@2 y4@3; [y1-y4@0 i s]; |
|
Linear with free time scores |
MODEL: i s | y1@0 y2@1 y3 y4; |
MODEL: i BY y1-y4@1; s BY y1@0 y2@1 y3 y4; [y1-y4@0 i s]; |
|
Quadratic |
MODEL: i s q | y1@0 y2@1 y3@2 y4@3;
|
MODEL: i BY y1-y4@1; s BY y1@0 y2@1 y3@2 y4@3; q BY y1@0 y2@1 y3@4 y4@9; [y1-y4@0 i s q]; |
|
Piecewise |
MODEL: i s1 | y1@0 y2@1 y3@2 y4@2 y5@2; i s2 | y1@0 y2@0 y3@0 y4@1 y5@2; |
MODEL: i BY y1-y4@1; s1 BY y1@0 y2@1 y3@2 y4@2 y5@2; s2 BY y1@0 y2@0 y3@0 y4@1 y5@2; [y1-y4@0 i s1 s2]; |
|
Linear for a censored outcome |
MODEL: i s | y1@0 y2@1 y3@2 y4@3;
|
MODEL: i BY y1-y4@1; s BY y1@0 y2@1 y3@2 y4@3; [y1-y4@0 i s]; |
|
Linear for a censored outcome and the inflation part of a censored outcome |
MODEL: i s | y1@0 y2@1 y3@2 y4@3; ii si |y1#1@0 y2#1@1 y3#1@2 y4#1@3;
|
MODEL: i BY y1-y4@1; s BY y1@0 y2@1 y3@2 y4@3; ii BY y1#1-y4#1@1; si BY y1#1@0 y2#1@1 y3#1@2 y4#1@3; [y1-y4@0 i s]; [y1#1-y4#1] (1); [ii@0 si]; |
|
Linear for a binary outcome with the Delta parameterization |
MODEL: i s | u1@0 u2@1 u3@2 u4@3;
|
MODEL: i BY u1-u4@1; s BY u1@0 u2@1 u3@2 u4@3; [u1$1-u4$1] (1); [i@0 s]; {u1@1 u2-u4}; |
|
Linear for a binary outcome with the Theta parameterization |
MODEL: i s | u1@0 u2@1 u3@2 u4@3;
|
MODEL: i BY u1-u4@1; s BY u1@0 u2@1 u3@2 u4@3; [u1$1-u4$1] (1); [i@0 s]; u1@1 u2-u4; |
|
Linear for a binary outcome with the logistic model |
MODEL: i s | u1@0 u2@1 u3@2 u4@3;
|
MODEL: i BY u1-u4@1; s BY u1@0 u2@1 u3@2 u4@3; [u1$1-u4$1] (1); [i@0 s]; |
|
Linear for a count outcome |
MODEL: i s | u1@0 u2@1 u3@2 u4@3;
|
MODEL: i BY u1-u4@1; s BY u1@0 u2@1 u3@2 u4@3; [u1-u4@0 i s]; |
|
Linear for a count outcome and the inflation part of a count outcome |
MODEL: i s | u1@0 u2@1 u3@2 u4@3; ii si | u1#1@0 u2#1@1 u3#1@2 u4#1@3;
|
MODEL: i BY u1-u4@1; s BY u1@0 u2@1 u3@2 u4@3; ii BY u1#1-u4#1@1; si BY u1#1@0 u2#1@1 u3#1@2 u4#1@3; [u1-u4@0 i s]; [u1#1-u4#1] (1); [ii@0 si]; |
|
Multiple group |
MODEL: i s | y1@0 y2@1 y3@2 y4@3; |
MODEL: i BY y1-y4@1; s BY y1@0 y2@1 y3@2 y4@3; [y1-y4@0 i s]; MODEL g1: [i s]; |
|
Multiple group for a binary outcome with the Delta parameterization
|
MODEL: i s | u1@0 u2@1 u3@2 u4@3; |
MODEL: i BY u1-u4@1; s BY u1@0 u2@1 u3@2 u4@3; [u1$1-u4$1] (1); {u1@1}; MODEL g1: [s]; {u2-u4}; |
|
Multiple group for a three-category outcome with the Delta parameterization
|
MODEL: i s | u1@0 u2@1 u3@2 u4@3; |
MODEL: i BY u1-u4@1; s BY u1@0 u2@1 u3@2 u4@3; [u1$1-u4$1] (1); [u1$2-u4$2] (2); MODEL g1: [s]; {u2-u4}; |
|
Multiple group for a binary outcome with the Theta parameterization |
MODEL: i s | u1@0 u2@1 u3@2 u4@3; |
MODEL: i BY u1-u4@1; s BY u1@0 u2@1 u3@2 u4@3; [u1$1-u4$1] (1); u1@1; MODEL g1: [s]; u2-u4; |
|
Multiple group for a three-category outcome with the Theta parameterization
|
MODEL: i s | u1@0 u2@1 u3@2 u4@3; |
MODEL: i BY u1-u4@1; s BY u1@0 u2@1 u3@2 u4@3; [u1$1-u4$1] (1); [u1$2-u4$2] (2); MODEL g1: [s]; u2-u4; |
|
Mixture |
MODEL: %OVERALL% i s | y1@0 y2@1 y3@2 y4@3;
|
MODEL: %OVERALL% i BY y1-y4@1; s BY y1@0 y2@1 y3@2 y4@3; [y1-y4@0 i s]; %c#1% [i s]; |
|
Mixture for a binary outcome |
MODEL: %OVERALL% i s | u1@0 u2@1 u3@2 u4@3;
|
MODEL: %OVERALL% i BY u1-u4@1; s BY u1@0 u2@1 u3@2 u4@3; [u1$1-u4$1] (1); [ i s]; %c#1% [i s]; %c#2% [i@0 ]; |
|
Multilevel |
MODEL: %WITHIN% iw sw | y1@0 y2@1 y3@2 y4@3; %BETWEEN% ib sb | y1@0 y2@1 y3@2 y4@3; |
MODEL: %WITHIN% iw BY y1-y4@1; sw BY y1@0 y2@1 y3@2 y4@3; %BETWEEN% ib BY y1-y4@1; sb BY y1@0 y2@1 y3@2 y4@3; [y1-y4@0 ib sb]; |
|
Multiple indicator |
MODEL: f1 BY y11 y21 (1); f2 BY y12 y22 (1); f3 BY y13 y23 (1); f4 BY y14 y24 (1); [y11 y12 y13 y14] (2); [y21 y22 y23 y24] (3); i s | f1@0 f2@1 f3@2 f4@3; |
MODEL: f1 BY y11 y21 (1); f2 BY y12 y22 (1); f3 BY y13 y23 (1); f4 BY y14 y24 (1); [y11 y12 y13 y14] (2); [y21 y22 y23 y24] (3); i BY f1-f4@1; s BY f1@0 f2@1 f3@2 f4@3; [f1-f4@0 i@0 s]; |
|
Multiple indicator for a binary outcome with the Delta parameterization |
MODEL: f1 BY u11 u21 (1); f2 BY u12 u22 (1); f3 BY u13 u23 (1); f4 BY u14 u24 (1); [u11$1 u12$1 u13$1 u14$1] (2); [u21$1 u22$1 u23$1 u24$1] (3); {u11-u21@1 u12-u24}; i s | f1@0 f2@1 f3@2 f4@3;
|
MODEL: f1 BY u11 u21 (1); f2 BY u12 u22 (1); f3 BY u13 u23 (1); f4 BY u14 u24 (1); [u11$1 u12$1 u13$1 u14$1] (2); [u21$1 u22$1 u23$1 u24$1] (3); {u11-u21@1 u12-u24}; i BY f1-f4@1; s BY f1@0 f2@1 f3@2 f4@3; [f1-f4@0 i@0 s]; |
|
Multiple indicator for a binary outcome with the Theta parameterization |
MODEL: f1 BY u11 u21 (1); f2 BY u12 u22 (1); f3 BY u13 u23 (1); f4 BY u14 u24 (1); [u11$1 u12$1 u13$1 u14$1] (2); [u21$1 u22$1 u23$1 u24$1] (3); u11-u21@1 u12-u24; i s | f1@0 f2@1 f3@2 f4@3;
|
MODEL: f1 BY u11 u21 (1); f2 BY u12 u22 (1); f3 BY u13 u23 (1); f4 BY u14 u24 (1); [u11$1 u12$1 u13$1 u14$1] (2); [u21$1 u22$1 u23$1 u24$1] (3); u11-u21@1 u12-u24; i BY f1-f4@1; s BY f1@0 f2@1 f3@2 f4@3; [f1-f4@0 i@0 s]; |
The defaults for the means/intercepts of the growth factors vary depending on the scale of the outcome variable as described below. The variances/residual variances and covariances/residual covariances of growth factors are free to be estimated for all outcomes as the default.
For continuous, censored, and count outcomes, the means/intercepts of the growth factors are free to be estimated. For a binary outcome, an ordered categorical (ordinal) outcome, the inflation part of a censored outcome, the inflation part of a count outcome, and a multiple indicator growth model, the mean/intercept of the intercept growth factor is fixed at zero. The means/intercepts of the slopes growth factors are free to be estimated.
In multiple group analysis for continuous, censored, and count outcomes, the means/intercepts of the growth factors are free to be estimated in all groups. In multiple group analysis for a binary outcome, an ordered categorical (ordinal) outcome, the inflation part of a censored outcome, the inflation part of a count outcome, and a multiple indicator growth model, the mean/intercept of the intercept growth factor is fixed at zero in the first group and is free to be estimated in the other groups. The means/intercepts of the slopes growth factors are free to be estimated in all groups.
In mixture models for continuous, censored, and count outcomes, the means/intercepts of the growth factors are free to be estimated in all classes. In mixture models for a binary outcome, an ordered categorical (ordinal) outcome, the inflation part of a censored outcome, the inflation part of a count outcome, and a multiple indicator growth model, the mean/intercept of the intercept growth factor is fixed at zero in the last class and is free to be estimated in the other classes. The means/intercepts of the slopes growth factors are free to be estimated in all classes.
The residual variances of continuous and censored outcome variables are free as the default. The inflated part of censored outcomes, binary outcomes, ordered categorical (ordinal) outcomes, count outcomes, and the inflated part of count outcomes have no variance parameters. An exception is the Theta parameterization used for binary and ordered categorical (ordinal) outcomes. In the Theta parameterization, residual variances are fixed at one at the first time point and are free at the other time points.
The AT option is used with TYPE=RANDOM to define a growth model with individually-varying times of observation for the outcome variable. AT is short for measured at. It is used in conjunction with the | symbol to name and define the random effect variables in a growth model which are referred to as growth factors.
Four types of growth models can be defined using AT and the | symbol: an intercept only model, a model with two growth factors, a model with three growth factors, and a model with four growth factors. The names of the random effect variables are specified on the left-hand side of the | symbol. The number of names determines which of the four models model will be estimated. One name is needed for an intercept only model and it refers to the intercept growth factor. Two names are needed for a model with two growth factors: the first one is for the intercept growth factor and the second one is for the slope growth factor that uses the time scores to the power of one. Three names are needed for a model with three growth factors: the first one is for the intercept growth factor; the second one is for the slope growth factor that uses the time scores to the power of one; and the third one is for the slope growth factor that uses the time scores to the power of two. Four names are needed for a model with four growth factors: the first one is for the intercept growth factor; the second one is for the slope growth factor that uses the time scores to the power of one; the third one is for the slope growth factor that uses the time scores to the power of two; and the fourth one is for the slope growth factor that uses the time scores to the power of three. Following are examples of how to specify these growth models:
intercpt | y1 y2 y3 y4 AT t1 t2 t3 t4;
intercpt slope1 | y1 y2 y3 y4 AT t1 t2 t3 t4;
intercpt slope1 slope2 | y1 y2 y3 y4 AT t1 t2 t3 t4;
intercpt slope1 slope2 slope3 | y1 y2 y3 y4 AT t1 t2 t3 t4;
where intercpt, slope1, slope2, and slope3 are the names of the intercept and slope growth factors; y1, y2, y3, and y4 are the outcome variables in the growth model; and t1, t2, t3, and t4 are observed variables in the data set that contain information on times of measurement. The TSCORES option of the VARIABLE command is used to identify the variables that contain information about individually-varying times of observation for the outcome in a growth model. The variables on the left-hand side of AT are paired with the variables on the right-hand side of AT.
The intercepts of the outcome variables are fixed at zero as the default. The residual variances of the outcome variables are free to be estimated as the default. The residual covariances of the outcome variables are fixed at zero as the default. The means, variances, and covariances of the intercept and slope growth factors are free as the default.
The | symbol is used in conjunction with TYPE=RANDOM to name and define the random slope variables in the model. The name on the left-hand side of the | symbol names the random slope variable. The statement on the right-hand side of the | symbol defines the random slope variable. Random slopes are defined using the ON or PON options. ON or PON statements used on the right-hand side of the | symbol may not use the asterisk (*) or @ symbols. Otherwise, the regular rules regarding ON and PON apply. The means and the variances of the random slope variables are free as the default. Covariances among random slope variables are fixed at zero as the default. Covariances between random slope variables and growth factors, latent variables defined using BY statements, and observed variables are fixed at zero as the default.
With TYPE=TWOLEVEL RANDOM and TYPE=CROSSCLASSIFIED RANDOM, the random slope variables are named and defined in the within part of the MODEL command and used in the between part of the MODEL command. For TYPE=THREELEVEL RANDOM, the random slope variables are named and defined in the within and between level 2 parts of the MODEL command. Random slope variables defined in within part of the MODEL command can be used in both the between level 2 and between level 3 parts of the MODEL command. Random slope variables defined in the between level 2 part of the MODEL command can be used only in the between level 3 part of the MODEL command.
For TYPE=THREELEVEL and TYPE=CROSSCLASSIFIED, random slope variables are between-level variables. For TYPE=TWOLEVEL, random slope variables are between-level variables unless specifically designated as having variation on both levels. This is done by placing an asterisk (*) after the name on the left-hand side of the | symbol as follows:
s* | y ON x;
where the asterisk (*) indicates that the random slope variable s has variation on both the within and between levels.
Following is an example of how to specify a random slope using the | symbol:
s | y ON x;
where s is a random slope in the regression of y on x where y is a continuous dependent variable and x is an independent variable. Both dependent and independent variables can be latent or observed variables.
Lists can be used on both the left-hand side of the | symbol and the left- and right-hand sides of ON and PON. Following is an example of how to specify a set of random slopes using the | symbol and PON:
s1-s3 | y1-y3 PON x1-x3;
where s1, s2, and s3 are random slopes in the regressions of y1 on x1, y2 on x2, and y3 on x3.
A random slope variable can refer to more than one slope by being used on the left-hand side of more than one | statement. In this case, the random slope variables are the same. For example,
s1 | y1 ON x1;
s1 | y2 ON x2;
defines the random slope, s1, to be the same in the regressions of y1 on x1 and y2 on x2.
Another example is,
s2 | y1 ON x1 x2;
which defines the random slope, s2, to be the same in the regressions of y1 on x1 and y1 on x2.
For TYPE=TWOLEVEL and TYPE=CROSSCLASSIFIED, the | symbol is used in conjunction with TYPE=RANDOM to name and define the random factor loading variables in the model. The names on the left-hand side of the | symbol name the random factor loading variables. The statements on the right-hand side of the | symbol define the random factor loading variables. Random factor loadings are defined using the BY option. BY statements used on the right-hand side of the | symbol may not use the asterisk (*) or @ symbol. Otherwise, the regular rules regarding BY apply. The means and the variances of the random factor loading variables are free as the default. Covariances between random factor loading variables and growth factors, latent variables defined using BY statements, and observed variables are fixed at zero as the default.
For TYPE=TWOLEVEL, the random factor loading variables are named and defined in the within part of the MODEL command and used in the between part of the MODEL command. For TYPE=CROSSCLASSIFIED, random factor loading variables that are named and defined in the level 2a part of the MODEL command can be used in the level 2b part of the MODEL command. Level 2a is the second cluster variable on the CLUSTER statement. Level 2b is the first cluster variable on the CLUSTER statement. Random factor loading variables are between-level variables. Following is an example of how to specify random factor loadings using the | symbol:
s1-s10 | f BY y1-y10;
f@1;
where s1 through s10 are random factor loadings for the factor f. All factor loadings are free. The metric of the factor is set by fixing the factor variance to one.
The | symbol is used in conjunction with TYPE=RANDOM to name and define random variance variables in the model. Random variances are available only for TYPE=TWOLEVEL with ESTIMATOR=BAYES. The name on the left-hand side of the | symbol names the random variance variable. The variable on the right-hand side of the | symbol specifies the variable that will have a random variance. The log of the random residual variance is used in the model. The asterisk (*) or @ symbols may not be used on the right-hand side of the | symbol. The means and the variances of the random variance variables are free as the default. Covariances among random variance variables are fixed at zero as the default. Covariances among random variance variables and growth factors, latent variables defined using BY statements, and observed variables are fixed at zero as the default. Following is an example of how to specify and random variance using the | symbol.
logv | y;
where logv is the random variance for the variable y.
The XWITH option is used with TYPE=RANDOM to define interactions between continuous latent variables or between a continuous latent variable and an observed variable. XWITH is short for multiplied with. It is used in conjunction with the | symbol to name and define interaction variables in a model. It is not available for TYPE=THREELEVEL or TYPE=CROSSCLASSIFIED. Following is an example of how to use XWITH and the | symbol to name and define an interaction:
int | f1 XWITH f2;
where int is the name of the interaction between f1 and f2. Interaction variables can be used only on the right-hand side of ON statements.
The XWITH option can be used to create an interaction variable that is the square of a latent variable. Following is an example of how this is specified:
fsquare | f XWITH f;
Latent variable interactions are estimated using maximum likelihood for all regular models as well as mixture models and multilevel models. Interactions are allowed between continuous latent variables and between a continuous latent variable and an observed variable. Factor indicators for the continuous latent variables can be continuous, censored, binary, ordered categorical (ordinal), counts, or combinations of these variable types. Observed variables in the interaction can be independent or mediating variables and the mediating variables can be censored, binary, ordered categorical (ordinal), counts, or combinations of these variable types. Dependent observed variables in the interaction can have missing data. In many cases, numerical integration is required in the maximum likelihood estimation of latent variable interactions. Numerical integration becomes increasingly more computationally demanding as the number of factors and the sample size increase.
Interactions between observed variables are handled using the DEFINE command
where an interaction variable is created via multiplication. If an observed
dependent variable has missing data, a latent variable can be created for this
observed variable and the procedure described above can be used.
Interactions between categorical latent variables and between a categorical
latent variable and an observed or continuous latent variable are handled using
mixture modeling.
Following is a table that summarizes ways of obtaining interactions for different variable types.
|
Types of Variables |
Interaction Options |
|
observed continuous with observed continuous |
DEFINE |
|
observed categorical with observed continuous |
DEFINE Multiple Group |
|
observed continuous with continuous latent |
XWITH |
|
observed categorical with continuous latent |
XWITH Multiple Group |
|
observed continuous with categorical latent |
MIXTURE |
|
observed categorical with categorical latent |
MIXTURE KNOWNCLASS |
|
continuous latent with continuous latent |
XWITH |
|
continuous latent with categorical latent |
MIXTURE |
|
categorical latent with categorical latent |
MIXTURE |
The MODEL INDIRECT command is used to request indirect and direct effects and their standard errors. Both the conventional indirect and direct effects used in the traditional mediation literature (see, e.g., MacKinnon, 2008; Hayes, 2013) and counterfactually-defined causal effects (see, e.g., Muthén, 2011; VanderWeele, 2015; Muthén & Asparouhov, 2015b; Muthén, Muthén, & Asparouhov, 2016) are available. The MODEL INDIRECT command is not available for TYPE=RANDOM, the CONSTRAINT option of the VARIABLE command, and TYPE=EFA.
Delta method standard errors for the indirect effects are computed as the default. Bootstrap standard errors for the indirect effects can be obtained by using the MODEL INDIRECT command in conjunction with the BOOTSTRAP option of the ANALYSIS command.
For conventional indirect and direct effects, the MODEL INDIRECT command can be used in conjunction with the STANDARDIZED option of the OUTPUT command to obtain standardized indirect effects and their standard errors. Bootstapped standard errors are available for the standardized indirect and direct effects when the BOOTSTRAP option is used.
MODEL INDIRECT can also be used in conjunction with the CINTERVAL option of the OUTPUT command to obtain confidence intervals and Bayes credibility intervals for the indirect and direct effects and the standardized indirect and direct effects. Three types of 95% and 99% confidence intervals can be obtained: symmetric, bootstrap, and bias-corrected bootstrap confidence intervals (MacKinnon, Lockwood, & Williams, 2004; MacKinnon, 2008). The bootstrapped distribution of each parameter estimate is used to determine the bootstrap and bias-corrected bootstrap confidence intervals. These intervals take non-normality of the parameter estimate distribution into account. As a result, they are not necessarily symmetric around the parameter estimate.
CONVENTIONAL INDIRECT AND DIRECT EFFECTS
Conventional indirect effects defined as products of regression coefficients are available for the case of a continuous, censored, binary, or ordered categorical (ordinal) mediator and a continuous, censored, binary, or ordered categorical (ordinal) outcome. Continuous mediators and outcomes can be observed continuous variables or continuous latent variables. For censored, binary, and ordered categorical (ordinal) mediators or outcomes, the latent response variables underlying these variables are used in the indirect and direct effects. These effects are available for multiple mediators and multiple outcomes. Total, total indirect, specific indirect, and direct effects used in traditional mediation modeling are obtained using the IND and VIA options. The IND option is used to request a specific indirect effect or a set of indirect effects. The VIA option is used to request a set of indirect effects that includes specific mediators.
The variable on the left-hand side of IND is the dependent variable in the indirect effect. The last variable on the right-hand side of IND is the independent variable in the indirect effect. Other variables on the right-hand side of IND are mediating variables. If there are no mediating variables included in the IND option, all indirect effects between the independent variable and dependent variable are computed. The total indirect effect is the sum of all indirect effects. The total effect is the sum of all indirect effects and the direct effect.
The variable on the left-hand side of VIA is the dependent variable in the indirect effect. The last variable on the right-hand side of VIA is the independent variable in the indirect effect. Other variables on the right-hand side of VIA are mediating variables. All indirect effects that go from the independent variable to the dependent variable and include the mediating variables are computed. The total indirect effect is the sum of all indirect effects.
Following is an example of the model shown in the picture above for which IND and VIA options will be specified.
MODEL:
y3 ON y1 y2;
y2 ON y1 x1 x2;
y1 ON x1 x2;
Following is an example of how MODEL INDIRECT can be used to request indirect effects using the IND option:
MODEL INDIRECT:
y3 IND y1 x1;
y3 IND y2 x1;
y3 IND x2;
The first IND statement requests the specific indirect effect from x1 to y1 to y3. The second IND statement requests the specific indirect effect from x1 to y2 to y3. The third IND statement requests all indirect effects from x2 to y3. These include x2 to y1 to y3, x2 to y2 to y3, and x2 to y1 to y2 to y3.
Following is an example of how MODEL INDIRECT can be used to request indirect effects using the VIA option:
MODEL INDIRECT:
y3 VIA y1 x1 ;
The VIA statement requests all indirect effects from x1 to y3 that are mediated by y1. These include x1 to y1 to y3 and x1 to y1 to y2 to y3.
Following is an example of how MODEL INDIRECT can be used to request total, total indirect, specific indirect, and direct effects:
MODEL INDIRECT:
y3 IND x1;
The IND statement requests all indirect effects from x1 to y3. These include x1 to y1 to y3, x1 to y2 to y3, and x1 to y1 to y2 to y3, the total effect, and the total indirect effect.
COUNTERFACTUALLY-DEFINED CAUSAL EFFECTS
Counterfactually-defined total natural indirect effects (TNIE), pure natural direct effects (PNDE), and total effects are available for continuous, binary, and ordered categorical (ordinal) mediators and continuous, binary, ordered categorical (ordinal) and count outcomes. Continuous mediators and outcomes can be observed continuous variables or continuous latent variables. The exposure variable can be binary or continuous. Counterfactually-defined total natural indirect effects, pure natural direct effects, and total effects are available for a single mediator. These effects are obtained using the IND and MOD options. The IND option is used to specify a specific indirect effect when there is no moderation. The MOD option is used to specify a specific indirect effect when there is moderation.
The IND option is used to specify a specific indirect effect when there is no moderation. Following is an example of how to specify the IND option with a binary exposure variable:
MODEL INDIRECT:
y IND m x;
where y is the outcome, m is the mediator, and x is a binary exposure variable. The outcome and mediator can be continuous latent variables.
When the exposure variable is continuous, two values must be given in parentheses following the exposure variable. The causal effects are computed comparing these two values. The default is one for the first value and zero for the second value corresponding to a binary exposure variable such as comparing a treatment group to a control group. Following is an example of how to specify the IND option with a continuous exposure variable:
MODEL INDIRECT:
y IND m x (1 -1);
where y is the outcome, m is the mediator, and x is the continuous exposure variable. The two values in parentheses following x are the values used to compute the causal effects, in this case, comparing 1 to -1, which represents an increase in x from -1 to 1. The outcome, mediator, and the exposure variable can be continuous latent variables.
The MOD option is used to specify a specific indirect effect when there is moderation. The MOD option can have three, four, or five arguments on the right-hand side of MOD. If the model contains continuous control variables, they should be centered for more meaningful results. If they are centered, indirect and direct effects are evaluated using their means. If they are not centered, indirect and direct effects are evaluated at the value zero.
The MOD option has three arguments when there is an interaction between the exposure variable and the mediator. Following is an example of how to specify the MOD option with three arguments:
MODEL INDIRECT:
y MOD m mx x;
where y is the outcome, m is the mediator, mx is the interaction between m and x, and x is a binary exposure variable. The variables must be given in this order. The outcome can be a continuous latent variable.
When a model contains a moderator variable in addition to an exposure and a mediator variable, a moderator plot is available showing the effects and their confidence intervals as a function of different values of the moderator variable. The MOD option with a moderator can have four or five arguments. The moderation plots are obtained by specifying TYPE=PLOT2 or TYPE=PLOT3 in the PLOT command.
The MOD option followed by four arguments has two specifications. The moderator can interact with either the mediator or the exposure variable. Following is an example of how to specify the MOD option with four arguments when the moderator interacts with the mediator:
MODEL INDIRECT:
y MOD m z (-1 1 0.1) mz x;
where y is the outcome, m is the mediator, z is the moderator, mz is the interaction between m and z, and x is a binary exposure variable. The variables must be given in this order. The numbers in parentheses following z are the lower limit, upper limit, and the increment to be used in evaluating and plotting the direct and indirect effects. The outcome can be a continuous latent variable.
Following is an example of how to specify the MOD option with four arguments when the moderator interacts with the mediator and the exposure variable is continuous:
MODEL INDIRECT:
y MOD m z (-1 1 0.1) mz x (1 -1);
where y is the outcome, m is the mediator, z is the moderator, mz is the interaction between m and z, and x is a continuous exposure variable. The variables must be given in this order. The numbers in parentheses following z are the lower limit, upper limit, and the increment to be used in evaluating and plotting the direct and indirect effects. The two values in parentheses following x are the values used to compute the causal effects, in this case, comparing 1 to -1, which represents an increase in x from -1 to 1. The outcome and the exposure variable can be continuous latent variables.
Following is an example of how to specify the MOD option with four arguments when the moderator interacts with the binary exposure variable:
MODEL INDIRECT:
y MOD m z (-1 1 0.1) xz x;
where y is the outcome, m is the mediator, z is the moderator, xz is the interaction between x and z, and x is a binary exposure variable. The variables must be given in this order. The numbers in parentheses following z are the lower limit, upper limit, and the increment to be used in evaluating and plotting the direct and indirect effects. The mediator and outcome can be continuous latent variables.
The MOD option has five arguments when a moderator interacts with both the mediator and the exposure variable. Following is an example of how to specify the MOD option with five arguments:
MODEL INDIRECT:
y MOD m z (-1 1 0.1) mz xz x;
where y is the outcome, m is the mediator, z is the moderator, mz is the interaction between m and z, xz is the interaction between x and z, and x is a binary exposure variable. The variables must be given in this order. The numbers in parentheses following z are the lower limit, upper limit, and the increment to be used in evaluating and plotting the direct and indirect effects. The outcome can be a continuous latent variable.
If the special direct effect referred to as the controlled direct effect is wanted, a value of the mediator must be given in parentheses following the mediator variable. Following is an example of how to specify the IND option with a binary exposure variable:
MODEL INDIRECT:
y IND m (2) x;
where y is the outcome, m is the mediator, and x is the binary exposure variable. The value in parentheses following m is used to compute the controlled direct effect.
The MODEL CONSTRAINT command is used to define linear and non-linear constraints on the parameters in the model and to create new parameters using the parameters in the model. These constraints can be implicit or explicit. The default setting for the INFORMATION option of the ANALYSIS command for MODEL CONSTRAINT is OBSERVED. The MODEL CONSTRAINT command is not available for TYPE=EFA.
LABELING THE PARAMETERS AND SELECTING VARIABLES
The MODEL CONSTRAINT command specifies parameter constraints using labels defined for parameters in the MODEL command, labels defined for parameters not in the MODEL command using the NEW option of the MODEL CONSTRAINT command, and names of observed variables that are identified using the CONSTRAINT option of the VARIABLE command. See Labeling Parameters to see how parameters are labeled using the MODEL command.
The NEW option is used to assign labels and starting values to parameters not in the analysis model. These parameters are used to constrain the parameters in the analysis model. The default starting value for these parameters is 0.5. Following is an example of how the NEW option is specified:
MODEL:
[y1-y3] (p1-p3);
MODEL CONSTRAINT:
NEW (c*.6);
p2 = p1 + c;
p3 = p1 + 2*c;
where c is a parameter that constrains the means to change linearly across the three variables. The value .6 following the asterisk (*) specifies that the value .6 will be used as a starting value for model estimation. If the analysis is a Monte Carlo simulation study, the value will also be used as a coverage value.
CONSTRAINT
CONSTRAINT = y1 u1;
where y1 and u1 are variables that can be used in the MODEL CONSTRAINT command.
DEFINING LINEAR AND NON-LINEAR CONSTRAINTS
Linear and non-linear constraints can be defined using the equal sign (=), the greater than sign (>), the less than sign (<), and all arithmetic operators and functions that are available in the DEFINE command with the exception of the absolute value function.
In the MODEL CONSTRAINT command, labels from the MODEL command and the NEW option of the MODEL CONSTRAINT command can be used on both the left-hand and right-hand sides of one or more parameter constraint statements. Variables listed on the CONSTRAINT option of the VARIABLE command can appear on the right-hand side of one or more parameter constraint statements. Following is an example of how to define an explicit constraint:
MODEL:
[y1-y3] (p1-p3);
MODEL CONSTRAINT:
p1 = p2**2 + p3**2;
where the parameter p1 is constrained to be equal to the sum of the squares of the p2 and p3 parameters.
Following is an example of how to define an implicit constraint where a function of parameters is constrained to be zero:
MODEL:
[y1-y5] (m1-m5);
MODEL CONSTRAINT:
0 = - m4 + m1*m3 - m2;
0 = exp(m3) - 1 - m2;
0 = m4 - m5;
Following is an example of how to define an implicit constraint where a parameter appears in a set of parameter constraints:
MODEL:
[y1-y4] (p1-p4);
MODEL CONSTRAINT:
p1 = p2**2 + p3**2;
p2 = p4;
The DO option provides a do loop and a double do loop to facilitate specifying a set of new parameters that are a function of the parameters of the model. Following is an example of how to specify a do loop:
MODEL:
y1 ON x1 (p1);
y1 ON x2 (p2);
y1 ON x3 (p3);
y2 ON x1 (q1);
y2 ON x2 (q2);
y2 ON x3 (q3);
MODEL CONSTRAINT:
NEW (ratio1-ratio3);
DO (1, 3) ratio# = p#/q#;
where the numbers in parentheses give the range of values for the do loop. The number sign (#) is replaced by these values during the execution of the do loop. Following are the new parameters that are created based on the DO option specified above:
ratio1 = p1/q1;
ratio2 = p2/q2;
ratio3 = p2/q3;
The DO option can also be used to place constraints on a set of parameters. Following is an example of how to use a do loop to constrain the residual variances of y1 through y4 to be greater than zero:
MODEL:
f BY y1-y4;
y1-y4 (p1-p4);
MODEL CONSTRAINT:
DO (1, 4) p# > 0;
where the numbers in parentheses give the range of values for the do loop. The number sign (#) is replaced by these values during the execution of the do loop. Following are the constraints that are placed on the model parameters based on the DO option specified above:
p1 > 0;
p2 > 0;
p3 > 0;
p4 > 0;
Following is an example of how to specify a double do loop:
MODEL:
y1 ON x1 (p1);
y2 ON x2 (p2);
y3 ON x3 (q3);
y4 ON x4 (q4);
MODEL CONSTRAINT:
DO ($,1,2) DO (%,3,4) p$ = q%;
where the numbers in parentheses give the range of values the double do loop will use. The numbers replace the symbol preceding them. Following are the constraints that are placed on the model parameters based on the DO option specified above:
p1 = q3;
p1 = q4;
p2 = q3;
p2 = q4;
The PLOT option is used to name the variables that will be plotted on the y-axis in the plots created using the LOOP option. Following is an example of how to specify the PLOT option:
PLOT (ind1 ind2);
where ind1 and ind2 are the variables that will be plotted on the y-axis in the plots created using the LOOP option.
The LOOP option is used in conjunction with the PLOT option to create plots of variables. For example, it is useful for plotting indirect effects with moderation and mediation (Preacher, Rucker, & Hayes, 2007), cross-level interactions in multilevel regression (Bauer & Curran, 2005), and sensitivity graphs for causal effect mediation modeling (Imai, Keele, & Tingley, 2010a; Muthén, 2011; Muthén, Muthén, & Asparouhov, 2016). Following is an example of how to specify the LOOP option:
LOOP (mod, -1, 1, 0.01);
where mod is a variable that will be used on the x-axis, the numbers -1 and 1 are the lower and upper values of mod, and 0.01 is the incremental value of mod to use in the computations. When mod appears in a MODEL CONSTRAINT statement involving a new parameter, that statement is evaluated for each value of mod specified by the LOOP option. For example, the first value of mod is -1; the second value of mod is -1 plus 0.01 or -0.99; the third value of mod is -0.99 plus 0.01 or -0.98; the last value of mod is 1. Plots are created with mod on the x-axis and the names in the PLOT option on the y-axis.
Following is an example of how to use the PLOT and LOOP options with the MODEL and MODEL CONSTRAINT commands:
MODEL:
y ON x (p1);
MODEL CONSTRAINT:
PLOT (ypred);
LOOP (age, 10, 50, 1);
ypred = p1*age;
Using TYPE=PLOT2 in the PLOT command, the plot of ypred and age can be viewed by choosing Loop plots from the Plot menu of the Mplus Editor. The plot presents the computed values along with a 95% confidence interval. For frequentist estimation, the default confidence interval uses plus and minus 1.96 times the standard error. The CINTERVAL option of the OUTPUT command can be used in conjunction with the BOOTSTRAP option of the ANALYSIS command to obtain bootstapped or bias-corrected bootstrap confidence intervals. For Bayesian estimation, the default is credibility intervals of the posterior distribution with equal tail percentages. The CINTERVAL option of the OUTPUT command can be used to obtain credibility intervals of the posterior distribution that give the highest posterior density.
The MODEL TEST command is used to test restrictions on the parameters in the MODEL and MODEL CONSTRAINT commands using the Wald chi-square test. These restrictions are defined using labels from the MODEL command and new parameters from the NEW option of the MODEL CONSTRAINT command. See Labeling Parameters to see how parameters are labeled using the MODEL command. See the NEW option to see how new parameters are named using this option. Variables listed on the CONSTRAINT statement of the VARIABLE command cannot be used in MODEL TEST. Model restrictions can be defined using the equal sign (=) and all arithmetic operators and functions that are available in the DEFINE command with the exception of the absolute value function.
Following is an example of how to test restrictions on the parameters in the MODEL command using MODEL TEST:
MODEL:
y ON x1 (p1)
x2 (p2)
x3 (p3);
MODEL TEST:
0 = p2 – p1;
0 = p3 – p1;
where in the MODEL command p1, p2, and p3 represent the regression coefficients for x1, x2, and x3, respectively. In the MODEL TEST command, a joint test of the equality of the three regression coefficients is carried out using the Wald test with two degrees of freedom. Note that having 0 = p3 - p2 in MODEL TEST is redundant and incorrect.
Following is an example of how to test a restriction on the parameters in the MODEL CONSTRAINT command using MODEL TEST:
MODEL:
y ON m1 (b1);
y ON m2 (b2);
m1 ON x1 (a1);
m2 ON x2 (a2);
MODEL CONSTRAINT:
NEW (ind1 ind2);
ind1 = a1*b1;
ind2 = a2*b2;
MODEL TEST:
0 = ind1 – ind2;
where in the MODEL command b1 and b2 represent the regression coefficients for m1 and m2 and a1 and a2 represent the regression coefficients for x1 and x2. In the MODEL CONSTRAINT command, two new parameters are defined. Ind1 is the indirect effect from x1 to y via m1. Ind2 is the indirect effect from x2 to y via m2. In the MODEL TEST command, a test of the equality of the two indirect effects is carried out using the Wald test with one degree of freedom.
The DO option provides a do loop and a double do loop to facilitate specifying a set of tests involving model parameters that will be jointly tested using the Wald test. Following is an example of how to specify a do loop:
MODEL:
y1 ON x1 (p1);
y1 ON x2 (p2);
y1 ON x3 (p3);
y2 ON x1 (q1);
y2 ON x2 (q2);
y2 ON x3 (q3);
MODEL TEST:
DO (1, 3) 0 = p# - q#;
where the numbers in parentheses give the range of values for the do loop. The number sign (#) is replaced by these values during the execution of the do loop. Following is the set of tests involving model parameters that will be jointly tested using the Wald test based on the DO option specified above:
0 = p1 – q1;
0 = p2 – q2;
0 = p3 – q3;
Following is an example of how to specify a double do loop:
MODEL:
y1 ON x1 (p1);
y1 ON x2 (p2);
y1 ON x3 (p3);
y2 ON x1 (q1);
y2 ON x2 (q2);
y2 ON x3 (q3);
MODEL TEST:
DO (#,1,3) DO ($,1,3) 0 = p# - q$;
where the numbers in parentheses give the range of values the double do loop will use. The numbers replace the symbol preceding them. Following is the set of tests involving model parameters that will be jointly tested using the Wald test based on the DO option specified above:
0 = p1 – q1;
0 = p1 – q2;
0 = p1 – q3;
0 = p2 – q1;
0 = p2 – q2;
0 = p2 – q3;
0 = p3 – q1;
0 = p3 – q2;
0 = p3 – q3;
THE MODEL PRIORS COMMAND
The MODEL PRIORS command is used with ESTIMATOR=BAYES to specify the prior distribution for each parameter. The default is to use diffuse (non-informative) priors. Following is a table that shows the distributions available and the default priors for different types of parameters:
|
Type of Parameter |
Distributions Available |
Default Priors |
|
Observed continuous dependent variable means/intercepts (nu) |
normal |
normal (0, infinity) |
|
Observed continuous dependent variable variances/residual variances (theta) |
inverse Gamma |
inverse Gamma (-1, 0) |
|
Observed categorical dependent variable thresholds (tau) |
normal uniform |
normal (0, infinity) |
|
Factor loadings (lambda) |
normal |
normal (0, infinity)* normal (0, 5)** |
|
Regression coefficients (beta) |
normal |
normal (0, infinity)* normal (0, 5)** |
|
Continuous latent variable means/intercepts (alpha) |
normal |
normal (0, infinity) |
|
Continuous latent variable variances/residual variances (psi) |
One latent variable inverse Gamma Gamma uniform lognormal normal
More than one latent variable inverse Wishart |
inverse Gamma (-1, 0)
inverse Wishart (0, -p-1)*** |
|
Categorical latent variable parameters (varies) |
Dirichlet |
Dirichlet (10, 10) |
* Continuous variables
** Categorical variables
*** Not available for GIBBS(RW)
For the normal distribution default, infinity is ten to the power of ten. For the inverse Gamma default, the settings imply a uniform prior ranging from minus infinity to plus infinity. For the inverse Wishart default, p is the dimension of the multivariate block of latent variables. For the Dirichlet default, the first number gives the number of observations to add to the class referred to and the second number gives the number of observations to add to the last class. For a discussion of priors, see Gelman et al. (2004), Browne and Draper (2006), and Gelman (2006).
ASSIGNING PRIORS TO PARAMETERS
Priors are assigned to the parameters using the tilde (~) symbol, which means distributed as, using the following distribution settings:
Normal – N
Lognormal – LN
Uniform – U
Inverse Gamma – IG
Gamma – G
Inverse Wishart – IW
Dirichlet – D
Each setting has two numbers in parentheses following the setting. For the normal and lognormal distributions, the first number is the mean and the second number is the variance. For the uniform distribution, the first number is the lower limit and the second number is upper limit. For the inverse Gamma distribution, the first number is the shape parameter and the second number is the scale parameter. For the Gamma distribution, the first number is the shape parameter and the second number is the inverse scale parameter. For the inverse Wishart distribution, the first number is used to form a covariance matrix and the second number is the degrees of freedom. For the Dirichlet distribution, the first number gives the number of observations to add to the class referred to and the second number gives the number of observations to add to the last class. For a technical description of the implementation of priors, see Asparouhov and Muthén (2010b).
In the MODEL PRIORS command, labels from the MODEL command are used to represent parameters for which prior distributions are specified. See Labeling Parameters to see how parameters are labeled using the MODEL command. Following is an example of how to assign priors to the factor loading parameters:
MODEL:
f BY y1-y10* (p1-p10);
f@1;
MODEL PRIORS:
p1-p10 ~ N (1, 0.5);
where parameters p1 through p10 have normal priors with mean one and variance 0.5.
The COVARIANCE option is used to assign a prior to the covariance between two parameters. Only normal priors are available. Covariance priors can be assigned to only factor loadings, regression coefficients, intercepts, and thresholds for binary variables. Following is an example of how to specify the COVARIANCE option:
MODEL:
y ON x1 (p1)
x2 (p2);
MODEL PRIORS:
p1 ~ N (10, 4);
p2 ~ N (6, 1);
COVARIANCE (p1, p2) = 0.5;
where the bivariate prior distribution of p1 and p2 has a covariance of 0.5 which corresponds to a correlation of 0.25 computed as 0.5 / (sqrt (4) * sqrt (1)).
The DO option provides a do loop and a double do loop to facilitate specifying the same prior for a set of parameters. With MODEL PRIORS it can be used with the DIFFERENCE option to assign priors to differences among a set of parameters. Following is an example of how to specify a do loop:
MODEL:
f1 BY y1-y20;
f2 BY y1-y10
y11-y20 (s1-s10);
MODEL PRIORS:
DO (1,10) s# ~ N (0,0.1);
where the numbers in parentheses give the range of values for the do loop. The number sign (#) is replaced by these values during the execution of the do loop. Following are the statements that are generated based on the DO option specified above:
s1 ~ N (0,0.1);
s2 ~ N (0,0.1);
s3 ~ N (0,0.1);
s4 ~ N (0,0.1);
s5 ~ N (0,0.1);
s6 ~ N (0,0.1);
s7 ~ N (0,0.1);
s8 ~ N (0,0.1);
s9 ~ N (0,0.1);
s10 ~ N (0,0.1);
Following is an example of how to specify a double do loop for a multiple group model:
MODEL:
f1 BY y1-y20;
f2 BY y1-y15
y16-y20 (s#_1-s#_5);
MODEL PRIORS:
DO (#,1,2) DO ($,1,5) s#_$ ~ N (0,0.1);
where the numbers in parentheses give the range of values the double do loop will use. The numbers replace the symbol preceding them. In this example, the first do loop refers to the two groups. Following are the statements that are generated based on the DO option specified above:
s1_1 ~ N (0,0.01);
s1_2 ~ N (0,0.01);
s1_3 ~ N (0,0.01);
s1_4 ~ N (0,0.01);
s1_5 ~ N (0,0.01);
s2_1 ~ N (0,0.01);
s2_2 ~ N (0,0.01);
s2_3 ~ N (0,0.01);
s2_4 ~ N (0,0.01);
s2_5 ~ N (0,0.01);
The DIFFERENCE option is used to assign priors to the difference between two parameters. Only normal priors are available. Difference priors can be assigned to only factor loadings, regression coefficients, intercepts, and thresholds for binary variables. Following is an example of how to specify the DIFFERENCE option:
MODEL:
y ON x1 (p1)
x2 (p2);
MODEL PRIORS:
DIFFERENCE (p1, p2) ~ N (0, 0.01);
where the difference between p1 and p2 has a normal prior with mean zero and variance 0.01.
The DO option provides a do loop to facilitate specifying the same expression for a set of parameters. The DO and DIFFERENCE options can be used together to simplify the assignment of priors to a large set of difference parameters for models with multiple groups and multiple time points. In Bayesian estimation, multiple group analysis is obtained using TYPE=MIXTURE and the KNOWNCLASS option. Following is an example of how to use the DO and DIFFERENCE options to assign priors to differences across groups among a set of parameters:
MODEL:
%OVERALL%
f BY y1-y5;
%c#1%
f BY y2-y5 (p12-p15);
%c#2%
f BY y2-y5 (p22-p25);
%c#3%
f BY y2-y5 (p32-p35);
MODEL PRIORS:
DO (2, 5) DIFFERENCE (p1#-p3#) ~ N (0, 0.01);
where the numbers in parentheses give the range of values for the do loop. The number sign (#) is replaced by these values during the execution of the do loop. Following are the differences that were assigned normal priors with mean zero and variance 0.01:
p12 - p22
p12 - p32
p22 - p32
p13 - p23
p13 - p33
p23 - p33
p14 - p24
p14 - p34
p24 - p34
p15 - p25
p15 - p35
p25 - p35
The MODEL command is used to describe the analysis model using the options described in the previous sections. This section discusses variations of the MODEL command for use with multiple group models, mixture models, multilevel models, and models for generating data for Monte Carlo simulations studies.
MODEL:
The MODEL command is used to describe the analysis model for a single group analysis and the overall analysis model for multiple group analysis.
MODEL followed by a label is used to describe the group-specific analysis models in multiple group analysis and the analysis model for each categorical latent variable in mixture modeling when there are more than one categorical latent variable in the analysis.
In multiple group analysis, MODEL followed by a label is used to describe differences between the overall analysis model described in the MODEL command and the analysis model for each group. Labels are defined using the GROUPING option of the VARIABLE command for raw data in a single file, by the FILE option of the DATA command for raw data in separate files, and by the program for summary data. MODEL followed by a label is used in conjunction with the %WITHIN% and %BETWEEN% specifications in multiple group multilevel analysis.
In mixture modeling, MODEL followed by a label is used to describe the analysis model for each categorical latent variable when there are more than one categorical latent variable in the analysis and for combinations of categorical latent variables when there are more than two categorical latent variables in the analysis. Labels are defined by using the names of the categorical latent variables.
When there are more than one categorical latent variable in the model, the class-specific parts of the model for each categorical latent variable must be specified within a MODEL command for that categorical latent variable. The %OVERALL% specification is not included in the MODEL commands for each categorical latent variable. Following is an example of how to specify the MODEL command when there are more than one categorical latent variable in the model:
MODEL c1:
%c1#1%
%c1#2%
where the class-specific parts of the model for c1 is specified after MODEL c1.
When there are more than two categorical latent variables in the model, MODEL commands for pairs of categorical latent variables are allowed. These are used to specify parameters that are specific to the combinations of classes for those two categorical latent variables. Categorical latent variables can be combined in sets involving all but one categorical latent variable. For example, with three categorical latent variables c1, c2, and c3, combinations of up to two categorical latent variables are allowed. Following is an example of how this is specified:
MODEL c1.c2:
%c1#1.c2#1%
where %c1#1.c2#1% refers to a combination of class 1 for c1 and class 1 for c2.
%OVERALL%
%class label%
The MODEL command used in conjunction with %OVERALL% and %class label% is used to describe the overall and class-specific models for mixture models. Statements following %OVERALL% refer to the model common to all latent classes. Statements following %class label% refer to class-specific model statements.
Class labels are created by adding to the name of the categorical latent variable a number sign (#) followed by the class number. For example, if c is a categorical latent variable with two latent classes, the class labels are c#1 and c#2.
%WITHIN%
%BETWEEN%
%BETWEEN label%
The MODEL command used in conjunction with %WITHIN%, %BETWEEN%, and %BETWEEN label% is used to describe the individual-level and cluster-level models for multilevel modeling. For TYPE=TWOLEVEL, the statements following %WITHIN% describe the individual-level model and the statements following %BETWEEN% describe the cluster-level model. With multilevel mixture models, the %OVERALL% and %class label% specifications are used with the %WITHIN% and %BETWEEN% specifications to describe the mixture part of the model.
For TYPE=THREELEVEL and TYPE=CROSSCLASSIFIED, the statements following %WITHIN% describe the individual-level model and the statements following %BETWEEN label% describe the cluster-level model. The label is a cluster variable from the CLUSTER option.
The MODEL POPULATION command is used to provide the population parameter values to be used in data generation using the options of the MODEL command described earlier. The MODEL POPULATION command has variations for use with multiple group models, mixture models, and multilevel models. These are described below.
In the MODEL POPULATION command, each parameter in the model must be specified followed by the @ symbol or the asterisk (*) and the population parameter value. Any model parameter not specified will have the value of zero as the population parameter value.
Parameter estimates can be saved from a real data analysis using the ESTIMATES option of the SAVEDATA command and used in a subsequent Monte Carlo analysis as population parameter values. This is done by using the POPULATION option of the MONTECARLO command.
MODEL POPULATION:
The MODEL POPULATION command is used to provide the population parameter values to be used in data generation for single group analysis and the overall analysis model for multiple group analysis.
MODEL POPULATION-label:
MODEL POPULATION followed by a dash and a label is used to provide parameter values to be used in the generation of data for the group-specific analysis models in multiple group analysis and the analysis model for each categorical latent variable in mixture modeling when there are more than one categorical latent variable in the analysis.
In multiple group analysis, the label following the dash refers to the group. The first group is referred to by g1, the second group by g2, and so on. In mixture modeling, the label following the dash is the name of each categorical latent variable when there are more than one categorical latent variables in the generation of the data.
In addition, the NGROUPS option of the MONTECARLO command is used for the generation of data for multiple group Monte Carlo simulation studies.
MODEL POPULATION:
%OVERALL%
%class label%
MODEL POPULATION used in conjunction with %OVERALL% and %class label% is used to provide the population parameter values to be used in the generation of data for mixture models. Statements following %OVERALL% refer to the model common to all latent classes. Statements following %class label% refer to class-specific model statements. In addition, the GENCLASSES option of the MONTECARLO command is used for the generation of data for mixture models.
The statements in the overall part of the model include information about the means, variances, and covariances of the background variables and the specification of the overall model including information about parameters that do not vary across the classes. The class-specific parts of the model describe the parameters that vary across classes.
MODEL POPULATION:
%WITHIN%
%BETWEEN%
%BETWEEN label%
MODEL POPULATION used in conjunction with %WITHIN%, %BETWEEN%, and %BETWEEN label% is used to provide the population parameter values to be used in the generation of clustered data. For TYPE=TWOLEVEL, %WITHIN% is used to provide population parameter values for the individual-level model parameters. %BETWEEN% is used to provide population parameter values for the cluster-level model parameters. With multilevel mixture models, the %OVERALL% and %class label% specifications are used with the %WITHIN% and %BETWEEN% specifications to provide the population parameter values to be used in the generation of data for mixture models.
For TYPE=THREELEVEL and TYPE=CROSSCLASSIFIED, %WITHIN% is used to provide population parameter values for the individual-level model parameters. %BETWEEN label% is used to provide population parameter values for the cluster-level model parameters. For TYPE=THREELEVEL, the labels level2 and level3 are used to provide the level 2 and level 3 population parameter values. For TYPE=CROSSCLASSIFIED, the labels level2a and level2b are used to describe the level 2a and level 2b population parameter values.
In addition, the NCSIZES, CSIZES, BETWEEN, and WITHIN options of the MONTECARLO command are used for the generation of clustered data.
In Monte Carlo simulation studies, the MODEL command describes not only the analysis model but also provides values for each parameter that are used both as the population parameter values for computing coverage and as starting values in the estimation of the model. If the MODEL COVERAGE command is used, coverage is computed using the population parameter values specified in the MODEL COVERAGE command, and the values specified in the MODEL command are used only as starting values. The MODEL COVERAGE command has special options for multiple group models, mixture models, and multilevel models.
In MODEL COVERAGE, each parameter in the model must be specified followed by the @ symbol or the asterisk (*) and the population parameter value. Any model parameter not specified will have the value of zero as the population parameter value.
Parameter estimates can be saved from a real data analysis using the ESTIMATES option of the SAVEDATA command and used in a subsequent Monte Carlo analysis as population parameter values. This is done by using the COVERAGE option of the MONTECARLO command.
MODEL COVERAGE:
The MODEL COVERAGE command is used to provide the population parameter values to be used for computing coverage for single group analysis and the overall analysis model for multiple group analysis.
MODEL COVERAGE-label:
MODEL COVERAGE followed by a dash and a label is used in multiple group analysis to provide group-specific parameter values to be used in computing coverage. The label following the dash refers to the group. The first group is referred to by g1, the second group by g2, and so on. In mixture modeling, the label following the dash is the name of each categorical latent variable when there are more than one categorical latent variable.
MODEL COVERAGE:
%OVERALL%
%class label%
MODEL COVERAGE used in conjunction with %OVERALL% and %class label% is used to provide the population parameter values to be used in computing coverage. Statements following %OVERALL% refer to the model common to all latent classes. Statements following %class label% refer to class-specific model statements.
Class labels are created by adding to the name of the categorical latent variable a number sign (#) followed by the class number. For example, if c1 is a categorical latent variable with two latent classes, the class labels are c1#1 and c1#2.
The statements in the overall part of the model include information about the means, variances, and covariances of the background variables and the specification of the overall model including information about latent class parameters that do not vary across the classes. The class-specific parts of the model describe the latent class parameters that do vary across classes.
MODEL COVERAGE:
%WITHIN%
%BETWEEN%
%BETWEEN label%
MODEL COVERAGE used in conjunction with %WITHIN% and %BETWEEN% is used to provide the population parameter values to be used in computing coverage. For TYPE=TWOLEVEL, %WITHIN% is used to provide the population parameter values for the individual-level model parameters. %BETWEEN% is used to provide the population parameter values for the cluster-level model parameters.
For TYPE=THREELEVEL and TYPE=CROSSCLASSIFIED, %WITHIN% is used to provide population parameter values for the individual-level model parameters. %BETWEEN label% is used to provide population parameter values for the cluster-level model parameters. For TYPE=THREELEVEL, the labels level2 and level3 are used to provide the level 2 and level 3 population parameter values. For TYPE=CROSSCLASSIFIED, the labels level2a and level2b are used to describe the level 2a and level 2b population parameter values.
THE MODEL MISSING COMMAND
The MODEL MISSING command is used to provide information about the population parameter values for the missing data model to be used in the generation of data. The MODEL MISSING command has special options for multiple group models and for mixture models. The MISSING option of the MONTECARLO command is required for MODEL MISSING.
Each parameter in the model must be specified followed by the @ symbol or the asterisk (*) and the population parameter value. Any model parameter not specified will have the value of zero as the population parameter value.
Information about each variable listed in the MISSING statement of the MONTECARLO command must be included as part of the MODEL MISSING command. These variables must be dependent variables in the MODEL command. The probability of having missing data or not on these dependent variables is described by logistic regressions in the MODEL MISSING command. In the MODEL MISSING command, the missing data indicators use the same names as the dependent variables in the MODEL command. For each dependent variable, the intercept and slopes for all covariates must be specified for the logistic regression. The covariates in these logistic regressions can be both independent and dependent variables in the MODEL command. When a dependent variable in the MODEL command is used as a dependent variable in the logistic regression, it is a missing value indicator. When it is used as a covariate in the logistic regression, it is the original variable in the MODEL command. In the following example, in the first ON statement y1 is a missing value indicator variable. In the second ON statement, y1 is treated as the original variable.
MODEL MISSING:
y1 ON x;
y2 ON y1 x;
A dependent variable that is censored, categorical, or count is treated as a continuous covariate in the logistic regressions.
MODEL MISSING:
The MODEL MISSING command is used to provide information about the population parameter values for the missing data model to be used in the generation of data for single group analysis and the overall analysis model for multiple group analysis.
MODEL MISSING-label:
MODEL MISSING followed by a dash and a label is used in multiple group analysis to provide group-specific population parameter values for the missing data model to be used in the generation of data. The label following the dash refers to the group. The first group is referred to by g1, the second group by g2, and so on.
MODEL MISSING:
%OVERALL%
%class label%
MODEL MISSING used in conjunction with %OVERALL% and %class label% is used to provide the population parameter values for the missing data model to be used in the generation of data for mixture models. Statements following %OVERALL% refer to the model common to all latent classes. Statements following %class label% refer to class-specific model statements.
Class labels are created by adding to the name of the categorical latent variable a number sign (#) followed by the class number. For example, if c1 is a categorical latent variable with two latent classes, the class labels are c1#1 and c1#2.