CHAPTER 5
EXAMPLES: CONFIRMATORY FACTOR ANALYSIS AND STRUCTURAL EQUATION MODELING
Confirmatory factor analysis (CFA) is used to study the relationships between a set of observed variables and a set of continuous latent variables. When the observed variables are categorical, CFA is also referred to as item response theory (IRT) analysis (Fox, 2010; van der Linden, 2016). CFA with covariates (MIMIC) includes models where the relationship between factors and a set of covariates are studied to understand measurement invariance and population heterogeneity. These models can include direct effects, that is, the regression of a factor indicator on a covariate in order to study measurement non-invariance. Structural equation modeling (SEM) includes models in which regressions among the continuous latent variables are estimated (Bollen, 1989; Browne & Arminger, 1995; Joreskog & Sorbom, 1979). In all of these models, the latent variables are continuous. Observed dependent variable variables can be continuous, censored, binary, ordered categorical (ordinal), unordered categorical (nominal), counts, or combinations of these variable types.
CFA is a measurement model. SEM has two parts: a measurement model and a structural model. The measurement model for both CFA and SEM is a multivariate regression model that describes the relationships between a set of observed dependent variables and a set of continuous latent variables. The observed dependent variables are referred to as factor indicators and the continuous latent variables are referred to as factors. The relationships are described by a set of linear regression equations for continuous factor indicators, a set of censored normal or censored-inflated normal regression equations for censored factor indicators, a set of probit or logistic regression equations for binary or ordered categorical factor indicators, a set of multinomial logistic regression equations for unordered categorical factor indicators, and a set of Poisson or zero-inflated Poisson regression equations for count factor indicators.
The structural model describes three types of relationships in one set of multivariate regression equations: the relationships among factors, the relationships among observed variables, and the relationships between factors and observed variables that are not factor indicators. These relationships are described by a set of linear regression equations for the factors that are dependent variables and for continuous observed dependent variables, a set of censored normal or censored-inflated normal regression equations for censored observed dependent variables, a set of probit or logistic regression equations for binary or ordered categorical observed dependent variables, a set of multinomial logistic regression equations for unordered categorical observed dependent variables, and a set of Poisson or zero-inflated Poisson regression equations for count observed dependent variables. For logistic regression, ordered categorical variables are modeled using the proportional odds specification. Both maximum likelihood and weighted least squares estimators are available.
All CFA, MIMIC and SEM models can be estimated using the following special features:
· Single or multiple group analysis
· Missing data
· Complex survey data
· Latent variable interactions and non-linear factor analysis using maximum likelihood
· Random slopes
· Linear and non-linear parameter constraints
· Indirect effects including specific paths
· Maximum likelihood estimation for all outcome types
· Bootstrap standard errors and confidence intervals
· Wald chi-square test of parameter equalities
For continuous, censored with weighted least squares estimation, binary, and ordered categorical (ordinal) outcomes, multiple group analysis is specified by using the GROUPING option of the VARIABLE command for individual data or the NGROUPS option of the DATA command for summary data. For censored with maximum likelihood estimation, unordered categorical (nominal), and count outcomes, multiple group analysis is specified using the KNOWNCLASS option of the VARIABLE command in conjunction with the TYPE=MIXTURE option of the ANALYSIS command. The default is to estimate the model under missing data theory using all available data. The LISTWISE option of the DATA command can be used to delete all observations from the analysis that have missing values on one or more of the analysis variables. Corrections to the standard errors and chi-square test of model fit that take into account stratification, non-independence of observations, and unequal probability of selection are obtained by using the TYPE=COMPLEX option of the ANALYSIS command in conjunction with the STRATIFICATION, CLUSTER, and WEIGHT options of the VARIABLE command. The SUBPOPULATION option is used to select observations for an analysis when a subpopulation (domain) is analyzed. Latent variable interactions are specified by using the | symbol of the MODEL command in conjunction with the XWITH option of the MODEL command. Random slopes are specified by using the | symbol of the MODEL command in conjunction with the ON option of the MODEL command. Linear and non-linear parameter constraints are specified by using the MODEL CONSTRAINT command. Indirect effects are specified by using the MODEL INDIRECT command. Maximum likelihood estimation is specified by using the ESTIMATOR option of the ANALYSIS command. Bootstrap standard errors are obtained by using the BOOTSTRAP option of the ANALYSIS command. Bootstrap confidence intervals are obtained by using the BOOTSTRAP option of the ANALYSIS command in conjunction with the CINTERVAL option of the OUTPUT command. The MODEL TEST command is used to test linear restrictions on the parameters in the MODEL and MODEL CONSTRAINT commands using the Wald chi-square test.
Graphical displays of observed data and analysis results can be obtained using the PLOT command in conjunction with a post-processing graphics module. The PLOT command provides histograms, scatterplots, plots of individual observed and estimated values, plots of sample and estimated means and proportions/probabilities, and plots of item characteristic curves and information curves. These are available for the total sample, by group, by class, and adjusted for covariates. The PLOT command includes a display showing a set of descriptive statistics for each variable. The graphical displays can be edited and exported as a DIB, EMF, or JPEG file. In addition, the data for each graphical display can be saved in an external file for use by another graphics program.
Following is the set of CFA examples included in this chapter:
· 5.1: CFA with continuous factor indicators
· 5.2: CFA with categorical factor indicators
· 5.3: CFA with continuous and categorical factor indicators
· 5.4: CFA with censored and count factor indicators*
· 5.5: Item response theory (IRT) models*
· 5.6: Second-order factor analysis
· 5.7: Non-linear CFA*
· 5.8: CFA with covariates (MIMIC) with continuous factor indicators
· 5.9: Mean structure CFA for continuous factor indicators
· 5.10: Threshold structure CFA for categorical factor indicators
Following is the set of SEM examples included in this chapter:
· 5.11: SEM with continuous factor indicators
· 5.12: SEM with continuous factor indicators and an indirect effect for factors
· 5.13: SEM with continuous factor indicators and an interaction between two factors*
Following is the set of multiple group examples included in this chapter:
· 5.14: Multiple group CFA with covariates (MIMIC) with continuous factor indicators and no mean structure
· 5.15: Multiple group CFA with covariates (MIMIC) with continuous factor indicators and a mean structure
· 5.16: Multiple group CFA with covariates (MIMIC) with categorical factor indicators and a threshold structure
· 5.17: Multiple group CFA with covariates (MIMIC) with categorical factor indicators and a threshold structure using the Theta parameterization
· 5.18: Two-group twin model for continuous outcomes where factors represent the ACE components
· 5.19: Two-group twin model for categorical outcomes where factors represent the ACE components
Following is the set of examples included in this chapter that estimate models with parameter constraints:
· 5.20: CFA with parameter constraints
· 5.21: Two-group twin model for continuous outcomes using parameter constraints
· 5.22: Two-group twin model for categorical outcomes using parameter constraints
· 5.23: QTL sibling model for a continuous outcome using parameter constraints
Following is the set of exploratory structural equation modeling (ESEM) examples included in this chapter:
· 5.24: EFA with covariates (MIMIC) with continuous factor indicators and direct effects
· 5.25: SEM with EFA and CFA factors with continuous factor indicators
· 5.26: EFA at two time points with factor loading invariance and correlated residuals across time
· 5.27: Multiple-group EFA with continuous factor indicators
· 5.28: EFA with residual variances constrained to be greater than zero
· 5.29: Bi-factor EFA using ESEM
· 5.30: Bi-factor EFA with two items loading on only the general factor
Following is the set of Bayesian CFA examples included in this chapter:
· 5.31: Bayesian bi-factor CFA with two items loading on only the general factor and cross-loadings with zero-mean and small-variance priors
· 5.32: Bayesian MIMIC model with cross-loadings and direct effects with zero-mean and small-variance priors
· 5.33: Bayesian multiple group model with approximate measurement invariance using zero-mean and small-variance priors
* Example uses numerical integration in the estimation of the model. This can be computationally demanding depending on the size of the problem.
TITLE: this is an example of a CFA with continuous factor indicators
DATA: FILE IS ex5.1.dat;
VARIABLE: NAMES ARE y1-y6;
MODEL: f1 BY y1-y3;
f2 BY y4-y6;
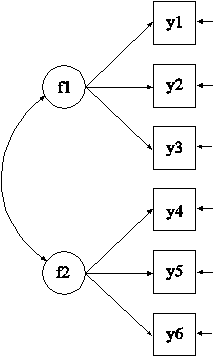
In this example, the confirmatory factor analysis (CFA) model with continuous factor indicators shown in the picture above is estimated. The model has two correlated factors that are each measured by three continuous factor indicators.
TITLE: this is an example of a CFA with continuous factor indicators
The TITLE command is used to provide a title for the analysis. The title is printed in the output just before the Summary of Analysis.
DATA: FILE IS ex5.1.dat;
The DATA command is used to provide information about the data set to be analyzed. The FILE option is used to specify the name of the file that contains the data to be analyzed, ex5.1.dat. Because the data set is in free format, the default, a FORMAT statement is not required.
VARIABLE: NAMES ARE y1-y6;
The VARIABLE command is used to provide information about the variables in the data set to be analyzed. The NAMES option is used to assign names to the variables in the data set. The data set in this example contains six variables: y1, y2, y3, y4, y5, y6. Note that the hyphen can be used as a convenience feature in order to generate a list of names.
MODEL: f1 BY y1-y3;
f2 BY y4-y6;
The MODEL command is used to describe the model to be estimated. Here the two BY statements specify that f1 is measured by y1, y2, and y3, and f2 is measured by y4, y5, and y6. The metric of the factors is set automatically by the program by fixing the first factor loading in each BY statement to 1. This option can be overridden. The intercepts and residual variances of the factor indicators are estimated and the residuals are not correlated as the default. The variances of the factors are estimated as the default. The factors are correlated as the default because they are independent (exogenous) variables. The default estimator for this type of analysis is maximum likelihood. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator.
TITLE: this is an example of a CFA with categorical factor indicators
DATA: FILE IS ex5.2.dat;
VARIABLE: NAMES ARE u1-u6;
CATEGORICAL ARE u1-u6;
MODEL: f1 BY u1-u3;
f2 BY u4-u6;
The difference between this example and Example 5.1 is that the factor indicators are binary or ordered categorical (ordinal) variables instead of continuous variables. The CATEGORICAL option is used to specify which dependent variables are treated as binary or ordered categorical (ordinal) variables in the model and its estimation. In the example above, all six factor indicators are binary or ordered categorical variables. The program determines the number of categories for each factor indicator. The default estimator for this type of analysis is a robust weighted least squares estimator (Muthén, 1984; Muthén, du Toit, & Spisic, 1997). With this estimator, probit regressions for the factor indicators regressed on the factors are estimated. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. An explanation of the other commands can be found in Example 5.1.
With maximum likelihood estimation, logistic regressions for the factor indicators regressed on the factors are estimated using a numerical integration algorithm. This is shown in Example 5.5. Note that numerical integration becomes increasingly more computationally demanding as the number of factors and the sample size increase.
TITLE: this is an example of a CFA with continuous and categorical factor indicators
DATA: FILE IS ex5.3.dat;
VARIABLE: NAMES ARE u1-u3 y4-y6;
CATEGORICAL ARE u1 u2 u3;
MODEL: f1 BY u1-u3;
f2 BY y4-y6;
The difference between this example and Example 5.1 is that the factor indicators are a combination of binary or ordered categorical (ordinal) and continuous variables instead of all continuous variables. The CATEGORICAL option is used to specify which dependent variables are treated as binary or ordered categorical (ordinal) variables in the model and its estimation. In the example above, the factor indicators u1, u2, and u3 are binary or ordered categorical variables whereas the factor indicators y4, y5, and y6 are continuous variables. The program determines the number of categories for each factor indicator. The default estimator for this type of analysis is a robust weighted least squares estimator. With this estimator, probit regressions are estimated for the categorical factor indicators, and linear regressions are estimated for the continuous factor indicators. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. With maximum likelihood estimation, logistic regressions are estimated for the categorical dependent variables using a numerical integration algorithm. Note that numerical integration becomes increasingly more computationally demanding as the number of factors and the sample size increase. An explanation of the other commands can be found in Example 5.1.
TITLE: this is an example of a CFA with censored and count factor indicators
DATA: FILE IS ex5.4.dat;
VARIABLE: NAMES ARE y1-y3 u4-u6;
CENSORED ARE y1-y3 (a);
COUNT ARE u4-u6;
MODEL: f1 BY y1-y3;
f2 BY u4-u6;
OUTPUT: TECH1 TECH8;
The difference between this example and Example 5.1 is that the factor indicators are a combination of censored and count variables instead of all continuous variables. The CENSORED option is used to specify which dependent variables are treated as censored variables in the model and its estimation, whether they are censored from above or below, and whether a censored or censored-inflated model will be estimated. In the example above, y1, y2, and y3 are censored variables. The a in parentheses following y1-y3 indicates that y1, y2, and y3 are censored from above, that is, have ceiling effects, and that the model is a censored regression model. The censoring limit is determined from the data. The COUNT option is used to specify which dependent variables are treated as count variables in the model and its estimation and whether a Poisson or zero-inflated Poisson model will be estimated. In the example above, u4, u5, and u6 are count variables. Poisson regressions are estimated for the count dependent variables and censored regressions are estimated for the censored dependent variables.
The default estimator for this type of analysis is maximum likelihood with robust standard errors using a numerical integration algorithm. Note that numerical integration becomes increasingly more computationally demanding as the number of factors and the sample size increase. In this example, two dimensions of integration are used with a total of 225 integration points. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. The OUTPUT command is used to request additional output not included as the default. The TECH1 option is used to request the arrays containing parameter specifications and starting values for all free parameters in the model. The TECH8 option is used to request that the optimization history in estimating the model be printed in the output. TECH8 is printed to the screen during the computations as the default. TECH8 screen printing is useful for determining how long the analysis takes. An explanation of the other commands can be found in Example 5.1.
In this example, four logistic IRT models are estimated: the generalized partial credit model (GPCM), the two-parameter logistic model (2PL), the three-parameter logistic model (3PL) with a guessing parameter, and the four-parameter logistic model (4PL) with a lower (guessing) parameter and an upper asymptote parameter. In all examples, a single continuous factor is measured by 20 categorical factor indicators.
TITLE: this is an example of a generalized partial credit item response theory (IRT) model
DATA: FILE IS ex5.5part1.dat;
VARIABLE: NAMES ARE u1-u20;
CATEGORICAL ARE u1-u20 (gpcm);
ANALYSIS: ESTIMATOR = MLR;
MODEL: f BY u1-u20*;
f@1;
OUTPUT: TECH1 TECH8;
PLOT: TYPE = PLOT3;
In the first part of the example shown above, the GPCM model is estimated. The CATEGORICAL option is used to specify which dependent variables are treated as binary or ordered categorical (ordinal) variables in the model and its estimation. In the example above, the factor indicators u1 through u20 are ordered categorical (ordinal) variables. The letters gpcm in parentheses specify that a GPCM model is estimated. The program determines the number of categories for each factor indicator. By specifying ESTIMATOR=MLR, a maximum likelihood estimator with robust standard errors using a numerical integration algorithm will be used. Note that numerical integration becomes increasingly more computationally demanding as the number of factors and the sample size increase. In this example, one dimension of integration is used with 15 integration points. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator.
In the MODEL command, the BY statement specifies that f is measured by u1 through u20. The asterisk (*) frees the first factor loading which is fixed at one as the default to define the metric of the factor. Instead the metric of the factor is defined by fixing the factor variance at one in line with IRT. For one-factor models with no covariates, results are presented both in a factor model parameterization and in a conventional IRT parameterization.
With the following MODEL command, a partial credit model is estimated:
MODEL: f BY u1-u20@1;
f*1;
The OUTPUT command is used to request additional output not included as the default. The TECH1 option is used to request the arrays containing parameter specifications and starting values for all free parameters in the model. The TECH8 option is used to request that the optimization history in estimating the model be printed in the output. TECH8 is printed to the screen during the computations as the default. TECH8 screen printing is useful for determining how long the analysis takes. The PLOT command is used to request graphical displays of observed data and analysis results. These graphical displays can be viewed after the analysis is completed using a post-processing graphics module. Item characteristic curves and information curves are available. When covariates are included in the model with direct effects on one or more factor indicators, item characteristic curves can be plotted for each value of the covariate to show differential item functioning (DIF). An explanation of the other commands can be found in Example 5.1.
TITLE: this is an example of a two-parameter logistic item response theory (IRT) model
DATA: FILE IS ex5.5part2.dat;
VARIABLE: NAMES ARE u1-u20;
CATEGORICAL ARE u1-u20;
ANALYSIS: ESTIMATOR = MLR;
MODEL: f BY u1-u20*;
f@1;
OUTPUT: TECH1 TECH8;
PLOT: TYPE = PLOT3;
In the second part of the example shown above, a two-parameter logistic model is estimated. The difference between the specification for the GPCM and the 2PL models is that nothing is placed in parentheses after the variable names in the CATEGORICAL option. The factor indicators u1 through u20 are binary variables. If the factor indicators are ordered categorical (ordinal) variables, the input is the same but a graded-response model is estimated.
TITLE: this is an example of a three-parameter logistic item response theory (IRT) model using priors for the guessing parameters
DATA: FILE = ex5.5part3.dat;
VARIABLE: NAMES = u1-u20;
CATEGORICAL = u1-u20(3pl);
ANALYSIS: ESTIMATOR = MLR;
MODEL: f BY u1-u20*;
f@1;
[u1$2-u20$2] (a1-a20);
OUTPUT: TECH1 TECH8;
PLOT: TYPE = PLOT3;
MODEL PRIORS:
a1-a20~N(1.386,1);
In the third part of the example shown above, a three-parameter logistic model is estimated. One difference between the specification for the GPCM and the 3PL models is that 3pl is placed in parentheses after the variable names in the CATEGORICAL option. The factor indicators u1 through u20 are binary variables. In addition, because convergence problems are common with the 3PL model, the MODEL PRIORS command is used to provide priors for the second thresholds. The second thresholds are parameters related to the guessing parameters which cannot be referred to directly. The first thresholds are referred to by adding $1 to the variable names. The second thresholds are referred to by adding $2 to the variable names. In the MODEL command, labels are given to the second thresholds. These labels are used in MODEL PRIORS to assign priors to the second thresholds. Prior mean values for the second thresholds of 1.386 correspond to guessing values of 0.25 (Asparouhov & Muthén, 2016).
TITLE: this is an example of a four-parameter logistic item response theory (IRT) model
using priors for the lower (guessing) and upper asymptote parameters
DATA: FILE = ex5.5part4.dat;
VARIABLE: NAMES = u1-u20;
CATEGORICAL = u1-u20(4pl);
ANALYSIS: ESTIMATOR = MLR;
MODEL: f BY u1-u20*;
f@1;
[u1$2-u20$2] (a1-a20);
[u1$3-u20$3] (b1-b20);
OUTPUT: TECH1 TECH8;
PLOT: TYPE = PLOT3;
MODEL PRIORS:
a1-a20~N(1.386,1);
b1-b20~N(-2,1);
In the fourth part of the example shown above, a four-parameter logistic model is estimated. One difference between the specification for the GPCM and the 4PL models is that 4pl is placed in parentheses after the variable names in the CATEGORICAL option. The factor indicators u1 through u20 are binary variables. In addition, because convergence problems are common with the 4PL model, the MODEL PRIORS command is used to provide priors for the second and third thresholds. The second and third thresholds are parameters related to the upper asymptote (guessing) and lower asymptote parameters, respectively, which cannot be referred to directly. The first thresholds are referred to by adding $1 to the variable names. The second thresholds are referred to by adding $2 to the variable names. The third thresholds are referred to by adding $3 to the variable names. In the MODEL command, labels are given to the second and third thresholds. These labels are used in MODEL PRIORS to assign priors to the second and third thresholds. Prior mean values for the second thresholds of 1.386 correspond to guessing values of 0.25. Prior mean values for the third thresholds of -2 correspond to upper asymptote values of 0.88 (Asparouhov & Muthén, 2016).
TITLE: this is an example of a second-order factor analysis
DATA: FILE IS ex5.6.dat;
VARIABLE: NAMES ARE y1-y12;
MODEL: f1 BY y1-y3;
f2 BY y4-y6;
f3 BY y7-y9;
f4 BY y10-y12;
f5 BY f1-f4;
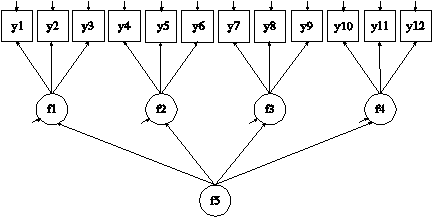
In this example, the second-order factor analysis model shown in the picture above is estimated. The factor indicators of the first-order factors f1, f2, f3, and f4 are continuous. The first-order factors are indicators of the second-order factor f5.
The first four BY statements specify that f1 is measured by y1, y2, and y3; f2 is measured by y4, y5, and y6; f3 is measured by y7, y8, and y9; and f4 is measured by y10, y11, and y12. The fifth BY statement specifies that the second-order factor f5 is measured by f1, f2, f3, and f4. The metrics of the first- and second-order factors are set automatically by the program by fixing the first factor loading in each BY statement to 1. This option can be overridden. The intercepts and residual variances of the first-order factor indicators are estimated and the residuals are not correlated as the default. The residual variances of the first-order factors are estimated as the default. The residuals of the first-order factors are not correlated as the default. The variance of the second-order factor is estimated as the default. The default estimator for this type of analysis is maximum likelihood. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. An explanation of the other commands can be found in Example 5.1.
TITLE: this is an example of a non-linear CFA
DATA: FILE IS ex5.7.dat;
VARIABLE: NAMES ARE y1-y5;
ANALYSIS: TYPE = RANDOM;
ALGORITHM = INTEGRATION;
MODEL: f BY y1-y5;
fxf | f XWITH f;
y1-y5 ON fxf;
OUTPUT: TECH1 TECH8;
In this example, a non-linear CFA model is estimated (McDonald, 1967). The factor indicators are quadratic functions of the factor. The TYPE option is used to describe the type of analysis that is to be performed. By selecting RANDOM, a model with a random effect will be estimated. By specifying ALGORITHM=INTEGRATION, a maximum likelihood estimator with robust standard errors using a numerical integration algorithm will be used. Note that numerical integration becomes increasingly more computationally demanding as the number of factors and the sample size increase. In this example, one dimension of integration is used with 15 integration points. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator.
The BY statement specifies that f is measured by y1 through y5. This specifies the linear part of the quadratic function. The | statement in conjunction with the XWITH option of the MODEL command is used to define the quadratic factor term. The name on the left-hand side of the | symbol names the quadratic factor term. The XWITH statement on the right-hand side of the | symbol defines the quadratic factor term fxf. The ON statement specifies the quadratic part of the quadratic function. The OUTPUT command is used to request additional output not included as the default. The TECH1 option is used to request the arrays containing parameter specifications and starting values for all free parameters in the model. The TECH8 option is used to request that the optimization history in estimating the model be printed in the output. TECH8 is printed to the screen during the computations as the default. TECH8 screen printing is useful for determining how long the analysis takes. An explanation of the other commands can be found in Example 5.1.
TITLE: this is an example of a CFA with covariates (MIMIC) with continuous factor indicators
DATA: FILE IS ex5.8.dat;
VARIABLE: NAMES ARE y1-y6 x1-x3;
MODEL: f1 BY y1-y3;
f2 BY y4-y6;
f1 f2 ON x1-x3;
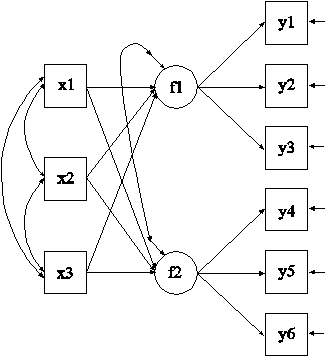
In this example, the CFA model with covariates (MIMIC) shown in the picture above is estimated. The two factors are regressed on three covariates.
The first BY statement specifies that f1 is measured by y1, y2, and y3. The second BY statement specifies that f2 is measured by y4, y5, and y6. The metric of the factors is set automatically by the program by fixing the first factor loading in each BY statement to 1. This option can be overridden. The intercepts and residual variances of the factor indicators are estimated and the residuals are not correlated as the default. The residual variances of the factors are estimated as the default. The residuals of the factors are correlated as the default because residuals are correlated for latent variables that do not influence any other variable in the model except their own indicators. The ON statement describes the linear regressions of f1 and f2 on the covariates x1, x2, and x3. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. An explanation of the other commands can be found in Example 5.1.
EXAMPLE 5.9: MEAN STRUCTURE CFA FOR CONTINUOUS FACTOR INDICATORS
TITLE: this is an example of a mean structure CFA
for continuous factor indicators
DATA: FILE IS ex5.9.dat;
VARIABLE: NAMES ARE y1a-y1c y2a-y2c;
MODEL: f1 BY y1a y1b@1 y1c@1;
f2 BY y2a y2b@1 y2c@1;
[y1a y1b y1c] (1);
[y2a y2b y2c] (2);
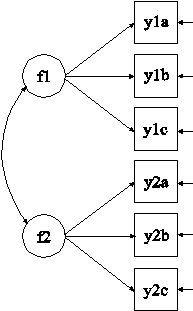
In this example, the CFA model in which two factors are measured by three equivalent tests forms shown in the picture above is estimated. The three equivalent test forms are referred to as a, b, and c.
The first BY statement specifies that f1 is measured by y1a, y1b, and y1c. The second BY statement specifies that f2 is measured by y2a, y2b, and y2c. The letters a, b, and c are used to represent three equivalent test forms, and 1 and 2 represent two different topics. The metric of the factors is set automatically by the program by fixing the first factor loading in each BY statement to 1. This option can be overridden. The second and third factor loadings for both factors are fixed at one using the @ option to reflect the hypothesis that the two test forms are equivalent. The intercepts and residual variances of the factor indicators are estimated and the residuals are not correlated as the default. The variances of the factors are estimated as the default. The covariance between f1 and f2 is estimated as the default because f1 and f2 are independent (exogenous) variables.
To reflect the hypothesis that the three test forms are equivalent with respect to their measurement intercepts, the first bracket statement specifies that the intercepts for y1a, y1b, and y1c are equal and the second bracket statement specifies that the intercepts for y2a, y2b, and y2c are equal. Equalities are designated by a number in parentheses. All parameters in a statement followed by the same number in parentheses are held equal. The means of the two factors are fixed at zero as the default. The default estimator for this type of analysis is maximum likelihood. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. An explanation of the other commands can be found in Example 5.1.
EXAMPLE 5.10: THRESHOLD STRUCTURE CFA FOR CATEGORICAL FACTOR INDICATORS
TITLE: this is an example of a threshold structure CFA for categorical factor indicators
DATA: FILE IS ex5.10.dat;
VARIABLE: NAMES ARE u1a-u1c u2a-u2c;
CATEGORICAL ARE u1a-u1c u2a-u2c;
MODEL: f1 BY u1a u1b@1 u1c@1;
f2 BY u2a u2b@1 u2c@1;
[u1a$1 u1b$1 u1c$1] (1);
[u2a$1 u2b$1 u2c$1] (2);
The difference between this example and Example 5.9 is that the factor indicators are binary or ordered categorical (ordinal) variables instead of continuous variables. The CATEGORICAL option is used to specify which dependent variables are treated as binary or ordered categorical (ordinal) variables in the model and its estimation. In the example above, all six factor indicators are binary or ordered categorical variables. The program determines the number of categories for each factor indicator. In this example, it is assumed that the factor indicators are binary variables with one threshold each.
For binary and ordered categorical factor indicators, thresholds are modeled rather than intercepts or means. The number of thresholds for a categorical variable is equal to the number of categories minus one. In the example above, the categorical variables are binary so they have one threshold. Thresholds are referred to by adding to the variable name a $ followed by a number. The thresholds of the factor indicators are referred to as u1a$1, u1b$1, u1c$1, u2a$1, u2b$1, and u2c$1. Thresholds are referred to in square brackets. To reflect the hypothesis that the three test forms are equivalent with respect to their measurement thresholds, the (1) after the first bracket statement specifies that the thresholds for u1a, u1b, and u1c are constrained to be equal and the (2) after the second bracket statement specifies that the thresholds for u2a, u2b, and u2c are constrained to be equal. The default estimator for this type of analysis is a robust weighted least squares estimator. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. With maximum likelihood, logistic regressions are estimated using a numerical integration algorithm. Note that numerical integration becomes increasingly more computationally demanding as the number of factors and the sample size increase. An explanation of the other commands can be found in Examples 5.1 and 5.9.
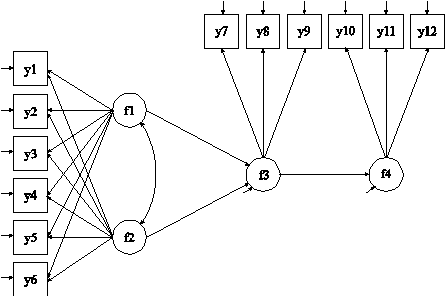
TITLE: this is an example of a SEM with continuous factor indicators
DATA: FILE IS ex5.11.dat;
VARIABLE: NAMES ARE y1-y12;
MODEL: f1 BY y1-y3;
f2 BY y4-y6;
f3 BY y7-y9;
f4 BY y10-y12;
f4 ON f3;
f3 ON f1 f2;
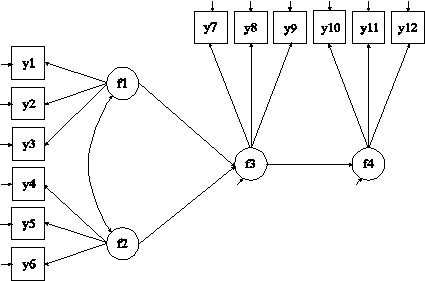
In this example, the SEM model with four continuous latent variables shown in the picture above is estimated. The factor indicators are continuous variables.
The first BY statement specifies that f1 is measured by y1, y2 and y3. The second BY statement specifies that f2 is measured by y4, y5, and y6. The third BY statement specifies that f3 is measured by y7, y8, and y9. The fourth BY statement specifies that f4 is measured by y10, y11, and y12. The metric of the factors is set automatically by the program by fixing the first factor loading in each BY statement to 1. This option can be overridden. The intercepts and residual variances of the factor indicators are estimated and the residuals are not correlated as the default. The variances of the factors are estimated as the default. The covariance between f1 and f2 is estimated as the default because f1 and f2 are independent (exogenous) variables. The other factor covariances are not estimated as the default.
The first ON statement describes the linear regression of f4 on f3. The second ON statement describes the linear regression of f3 on f1 and f2. The default estimator for this type of analysis is maximum likelihood. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. An explanation of the other commands can be found in Example 5.1.
TITLE: this is an example of a SEM with continuous factor indicators and an indirect effect for factors
DATA: FILE IS ex5.12.dat;
VARIABLE: NAMES ARE y1-y12;
MODEL: f1 BY y1-y3;
f2 BY y4-y6;
f3 BY y7-y9;
f4 BY y10-y12;
f4 ON f3;
f3 ON f1 f2;
MODEL INDIRECT:
f4 IND f3 f1;
The difference between this example and Example 5.11 is that an indirect effect is estimated. Indirect effects and their standard errors can be requested using the MODEL INDIRECT command. Total indirect, specific indirect, and total effects are specified by using the IND and VIA statements. Total effects include all indirect effects and the direct effect. The IND statement is used to request a specific indirect effect or set of indirect effects. The VIA statement is used to request a set of indirect effects that include specific mediators.
In the IND statement above, the variable on the left-hand side of IND is the dependent variable. The last variable on the right-hand side of IND is the independent variable. Other variables on the right-hand side of IND are mediating variables. The IND statement requests the specific indirect effect from f1 to f3 to f4. The default estimator for this type of analysis is maximum likelihood. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. An explanation of the other commands can be found in Examples 5.1 and 5.11.
TITLE: this is an example of a SEM with continuous factor indicators and an interaction between two latent variables
DATA: FILE IS ex5.13.dat;
VARIABLE: NAMES ARE y1-y12;
ANALYSIS: TYPE = RANDOM;
ALGORITHM = INTEGRATION;
MODEL: f1 BY y1-y3;
f2 BY y4-y6;
f3 BY y7-y9;
f4 BY y10-y12;
f4 ON f3;
f3 ON f1 f2;
f1xf2 | f1 XWITH f2;
f3 ON f1xf2;
OUTPUT: TECH1 TECH8;
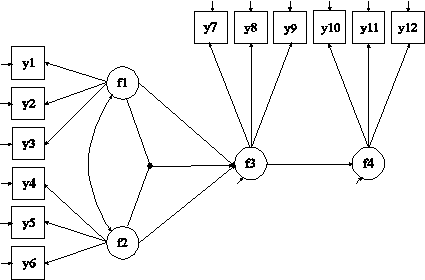
The difference between this example and Example 5.11 is that an interaction between two latent variables is included in the model. The interaction is shown in the picture above as a filled circle. The model is estimated using maximum likelihood (Klein & Moosbrugger, 2000).
The TYPE option is used to describe the type of analysis that is to be performed. By selecting RANDOM, a model with a random effect will be estimated. By specifying ALGORITHM=INTEGRATION, a maximum likelihood estimator with robust standard errors using a numerical integration algorithm will be used. Note that numerical integration becomes increasingly more computationally demanding as the number of factors and the sample size increase. In this example, two dimensions of integration are used with a total of 225 integration points. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator.
Latent variable interactions are specified by using the | statement in conjunction with the XWITH option of the MODEL command. The name on the left-hand side of the | symbol names the latent variable interaction. The XWITH statement on the right-hand side of the | symbol defines the latent variable interaction. The latent variable f1xf2 is the interaction between f1 and f2. The last ON statement uses the latent variable interaction as an independent variable. The OUTPUT command is used to request additional output not included as the default. The TECH1 option is used to request the arrays containing parameter specifications and starting values for all free parameters in the model. The TECH8 option is used to request that the optimization history in estimating the model be printed in the output. TECH8 is printed to the screen during the computations as the default. TECH8 screen printing is useful for determining how long the analysis takes. An explanation of the other commands can be found in Examples 5.1 and 5.11.
EXAMPLE 5.14: MULTIPLE GROUP CFA WITH COVARIATES (MIMIC) WITH CONTINUOUS FACTOR INDICATORS AND NO MEAN STRUCTURE
TITLE: this is an example of a multiple group CFA with covariates (MIMIC) with continuous factor indicators and no mean structure
DATA: FILE IS ex5.14.dat;
VARIABLE: NAMES ARE y1-y6 x1-x3 g;
GROUPING IS g (1 = male 2 = female);
ANALYSIS: MODEL = NOMEANSTRUCTURE;
INFORMATION = EXPECTED;
MODEL: f1 BY y1-y3;
f2 BY y4-y6;
f1 f2 ON x1-x3;
MODEL female:
f1 BY y3;
The difference between this example and Example 5.8 is that this is a multiple group rather than a single group analysis. The GROUPING option is used to identify the variable in the data set that contains information on group membership when the data for all groups are stored in a single data set. The information in parentheses after the grouping variable name assigns labels to the values of the grouping variable found in the data set. In the example above, observations with g equal to 1 are assigned the label male, and individuals with g equal to 2 are assigned the label female. These labels are used in conjunction with the MODEL command to specify model statements specific to each group.
The NOMEANSTRUCTURE setting for the MODEL option of the ANALYSIS command is used with TYPE=GENERAL to specify that means, intercepts, and thresholds are not included in the analysis model. As a result, a covariance structure model is estimated. The INFORMATION option is used to select the estimator of the information matrix to be used in computing standard errors when the ML or MLR estimators are used for analysis. The default is the observed information matrix. In this example, the expected information matrix is used in line with conventional covariance structure analysis.
In multiple group analysis, two variations of the MODEL command are used. They are MODEL and MODEL followed by a label. MODEL describes the overall model to be estimated for each group. The factor loading measurement parameters are held equal across groups as the default to specify measurement invariance. MODEL followed by a label describes differences between the overall model and the model for the group designated by the label. In the group-specific MODEL command for females, the factor loading for variable y3 and factor f1 is specified to be free and not equal to the same factor loading for males. The default estimator for this type of analysis is maximum likelihood. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. An explanation of the other commands can be found in Examples 5.1 and 5.8.
EXAMPLE 5.15: MULTIPLE GROUP CFA WITH COVARIATES (MIMIC) WITH CONTINUOUS FACTOR INDICATORS AND A MEAN STRUCTURE
TITLE: this is an example of a multiple group CFA with covariates (MIMIC) with continuous factor indicators and a mean structure
DATA: FILE IS ex5.15.dat;
VARIABLE: NAMES ARE y1-y6 x1-x3 g;
GROUPING IS g (1 = male 2 = female);
MODEL: f1 BY y1-y3;
f2 BY y4-y6;
f1 f2 ON x1-x3;
MODEL female:
f1 BY y3;
[y3];
The difference between this example and Example 5.14 is that means are included in the model. In multiple group analysis, when a model includes a mean structure, both the intercepts and factor loadings of the continuous factor indicators are held equal across groups as the default to specify measurement invariance. The intercepts of the factors are fixed at zero in the first group and are free to be estimated in the other groups as the default. The group-specific MODEL command for females specifies that the intercept of y3 for females is free and not equal to the intercept for males. Intercepts are referred to by using square brackets. The default estimator for this type of analysis is maximum likelihood. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. An explanation of the other commands can be found in Examples 5.1, 5.8, and 5.14.
EXAMPLE 5.16: MULTIPLE GROUP CFA WITH COVARIATES (MIMIC) WITH CATEGORICAL FACTOR INDICATORS AND A THRESHOLD STRUCTURE
TITLE: this is an example of a multiple group CFA with covariates (MIMIC) with categorical factor indicators and a threshold structure
DATA: FILE IS ex5.16.dat;
VARIABLE: NAMES ARE u1-u6 x1-x3 g;
CATEGORICAL ARE u1-u6;
GROUPING IS g (1 = male 2 = female);
MODEL: f1 BY u1-u3;
f2 BY u4-u6;
f1 f2 ON x1-x3;
MODEL female:
f1 BY u3;
[u3$1];
{u3@1};
The difference between this example and Example 5.15 is that the factor indicators are binary or ordered categorical (ordinal) variables instead of continuous variables. For multiple-group CFA with categorical factor indicators, see Muthén and Christoffersson (1981) and Muthén and Asparouhov (2002).
The CATEGORICAL option is used to specify which dependent variables are treated as binary or ordered categorical (ordinal) variables in the model and its estimation. In the example above, all six factor indicators are binary or ordered categorical variables. The program determines the number of categories for each factor indicator.
For binary and ordered categorical factor indicators, thresholds are modeled rather than intercepts or means. The number of thresholds for a categorical variable is equal to the number of categories minus one. In the above example, u3 is a binary variable with two categories. Thresholds are referred to by adding to the variable name a $ followed by a number. The threshold for u3 is u3$1. Thresholds are referred to in square brackets. When a model includes a mean structure, the thresholds of the factor indicators are held equal across groups as the default to specify measurement invariance. In the group-specific MODEL command for females, the threshold and factor loading of u3 for females are specified to be free and not equal to the threshold and factor loading for males.
Because the factor indicators are categorical, scale factors are required for multiple group analysis when the default Delta parameterization is used. Scale factors are referred to using curly brackets ({}). By default, scale factors are fixed at one in the first group and are free to be estimated in the other groups. When a threshold and a factor loading for a categorical factor indicator are free across groups, the scale factor for that variable must be fixed at one in all groups for identification purposes. Therefore, the scale factor for u3 is fixed at one for females.
The default estimator for this type of analysis is a robust weighted least squares estimator. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. With maximum likelihood, logistic regressions are estimated using a numerical integration algorithm. Note that numerical integration becomes increasingly more computationally demanding as the number of factors and the sample size increase. An explanation of the other commands can be found in Examples 5.1, 5.8, 5.14, and 5.15.
TITLE: this is an example of a multiple group CFA with covariates (MIMIC) with categorical factor indicators and a threshold structure using the Theta parameterization
DATA: FILE IS ex5.17.dat;
VARIABLE: NAMES ARE u1-u6 x1-x3 g;
CATEGORICAL ARE u1-u6;
GROUPING IS g (1 = male 2 = female);
ANALYSIS: PARAMETERIZATION = THETA;
MODEL: f1 BY u1-u3;
f2 BY u4-u6;
f1 f2 ON x1-x3;
MODEL female:
f1 BY u3;
[u3$1];
u3@1;
The difference between this example and Example 5.16 is that the Theta parameterization is used instead of the Delta parameterization. In the Delta parameterization, scale factors are allowed to be parameters in the model, but residual variances for latent response variables of observed categorical dependent variables are not. In the alternative Theta parameterization, residual variances for latent response variables are allowed to be parameters in the model but scale factors are not. The Theta parameterization is selected by specifying PARAMETERIZATION=THETA in the ANALYSIS command.
When the Theta parameterization is used, the residual variances for the latent response variables of the observed categorical dependent variables are fixed at one in the first group and are free to be estimated in the other groups as the default. When a threshold and a factor loading for a categorical factor indicator are free across groups, the residual variance for the variable must be fixed at one in these groups for identification purposes. In the group-specific MODEL command for females, the residual variance for u3 is fixed at one. An explanation of the other commands can be found in Examples 5.1, 5.8, 5.14, 5.15, and 5.16.
TITLE: this is an example of a two-group twin
model for continuous outcomes where
factors represent the ACE components
DATA: FILE = ex5.18.dat;
VARIABLE: NAMES = y1 y2 g;
GROUPING = g (1 = mz 2 = dz);
ANALYSIS: MODEL = NOCOVARIANCES;
MODEL: [y1-y2] (1);
y1-y2@0;
a1 BY y1* (2);
a2 BY y2* (2);
c1 BY y1* (3);
c2 BY y2* (3);
e1 BY y1* (4);
e2 BY y2* (4);
a1-e2@1;
[a1-e2@0];
a1 WITH a2@1;
c1 WITH c2@1;
MODEL dz: a1 WITH a2@.5;
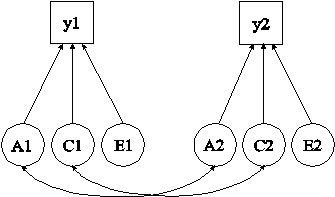
In this example, the univariate twin model shown in the picture above is estimated. This is a two-group twin model for a continuous outcome where factors represent the ACE components (Neale & Cardon, 1992). The variables y1 and y2 represent a univariate outcome for each member of the twin pair. The A factors represent the additive genetic components which correlate 1.0 for monozygotic twin pairs and 0.5 for dizygotic twin pairs. The C factors represent common environmental effects which correlate 1.0 for all twin pairs. The E factors represent uncorrelated environmental effects. A simpler alternative way of specifying this model is shown in Example 5.21 where parameter constraints are used instead of the A, C, and E factors.
Exogenous factors are correlated as the default. By specifying MODEL=NOCOVARIANCES in the ANALYSIS command, all covariances in the model are fixed at zero. The WITH option of the MODEL command can be used to override the default for selected covariances as shown in the three WITH statements. In the MODEL command, the (1) following the first bracket statement specifies that the intercepts of y1 and y2 are held equal across twins. The second statement fixes the residual variances of y1 and y2 to zero. The residual variances of y1 and y2 are instead captured by the loadings of the E factors. The six BY statements are used to define the six factors. The asterisk (*) is used to free the factor loadings because the default is that the factor loading for the first factor indicator is fixed at one. The loadings for the A, C, and E factors are held equal across twins by placing (2) following the two BY statements for the A factors, (3) following the two BY statements for the C factors, and (4) following the two BY statements for the E factors. In the next two statements, the A, C, and E factor variances are fixed at one and the A, C, and E factor means are fixed at zero. Because the factor means are fixed at zero, the intercepts of y1 and y2 are their means.
The WITH statement for the A factors is used to fix the covariance (correlation) between the A factors to 1.0 for monozygotic twin pairs. The group-specific MODEL command is used to fix the covariance between the A factors to 0.5 for the dizygotic twin pairs. The WITH statement for the C factors is used to fix the covariance between the C factors to 1. The default estimator for this type of analysis is maximum likelihood. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. An explanation of the other commands can be found in Examples 5.1 and 5.14.
TITLE: this is an example of a two-group twin model for categorical outcomes where factors represent the ACE components
DATA: FILE = ex5.19.dat;
VARIABLE: NAMES = u1 u2 g;
CATEGORICAL = u1-u2;
GROUPING = g (1 = mz 2 = dz);
ANALYSIS: MODEL = NOCOVARIANCES;
MODEL: [u1$1-u2$1] (1);
a1 BY u1* (2);
a2 BY u2* (2);
c1 BY u1* (3);
c2 BY u2* (3);
a1-c2@1;
[a1-c2@0];
a1 WITH a2@1;
c1 WITH c2@1;
MODEL dz: a1 WITH a2@.5;
{u1-u2@1};
The difference between this example and Example 5.18 is that the outcomes are binary or ordered categorical instead of continuous variables. Because of this, the outcomes have no freely estimated residual variances and therefore the E factors are not part of the model. With categorical outcomes, the twin model is formulated for normally-distributed latent response variables underlying the categorical outcomes which are also called liabilities. This model is referred to as the threshold model for liabilities (Neale & Cardon, 1992). More complex examples of such models are given in Prescott (2004). A simpler alternative way of specifying this model is shown in Example 5.22 where parameter constraints are used instead of the A and C factors.
The CATEGORICAL option is used to specify which dependent variables are treated as binary or ordered categorical (ordinal) variables in the model and its estimation. In the example above, u1 and u2 are binary or ordered categorical variables. The program determines the number of categories for each variable.
For binary and ordered categorical outcomes, thresholds are modeled rather than intercepts or means. The number of thresholds for a categorical variable is equal to the number of categories minus one. In the example above, the categorical variables are binary so they have one threshold. Thresholds are referred to by adding to the variable name a $ followed by a number. The thresholds of u1 and u2 are referred to as u1$1 and u2$1. Thresholds are referred to in square brackets. The (1) after the first bracket statement specifies that the thresholds for u1$1 and u2$1 are constrained to be equal.
Because the outcomes are categorical, scale factors are required for multiple group analysis when the default Delta parameterization is used. Scale factors are referred to using curly brackets ({}). By default, scale factors are fixed at one in the first group and are free to be estimated in the other groups. In this model where the variance contributions from the A and C factors are assumed equal across the two groups, the scale factors are fixed at one in both groups to represent the equality of variance for latent response variables underlying u1 and u2. The statement in curly brackets in the group-specific MODEL command specifies that the scale factors are fixed at one. The variance contribution from the E factor is a remainder obtained by subtracting the variance contributions of the A and C factors from the unit variance of the latent response variables underlying u1 and u2. These are obtained as part of the STANDARDIZED option of the OUTPUT command.
The default estimator for this type of analysis is a robust weighted least squares estimator. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. With maximum likelihood and categorical factor indicators, numerical integration is required. Note that numerical integration becomes increasingly more computationally demanding as the number of factors and the sample size increase. An explanation of the other commands can be found in Examples 5.1, 5.14, and 5.18.
TITLE: this is an example of a CFA with parameter
constraints
DATA: FILE = ex5.20.dat;
VARIABLE: NAMES = y1-y6;
MODEL: f1 BY y1
y2-y3(lam2-lam3);
f2 BY y4
y5-y6(lam5-lam6);
f1 (vf1);
f2 (vf2);
y1-y3 (ve1-ve3);
y4-y6 (ve4-ve6);
MODEL CONSTRAINT:
NEW(rel2 rel5 stan3 stan6);
rel2 = lam2**2*vf1/(lam2**2*vf1 + ve2);
rel5 = lam5**2*vf2/(lam5**2*vf2 + ve5);
rel5 = rel2;
stan3 = lam3*SQRT(vf1)/SQRT(lam3**2*vf1 + ve3);
stan6 = lam6*SQRT(vf2)/SQRT(lam6**2*vf2 + ve6);
0 = stan6 - stan3;
ve2 > ve5;
ve4 > 0;
OUTPUT: STANDARDIZED;
In this example, parameter constraints are used to estimate reliabilities, estimate standardized coefficients, constrain functions of parameters to be equal, and constrain parameters to be greater than a value. This example uses the model from Example 5.1.
The MODEL CONSTRAINT command specifies parameter constraints using labels defined for parameters in the MODEL command, labels defined for parameters not in the MODEL command using the NEW option of the MODEL CONSTRAINT command, and names of observed variables that are identified using the CONSTRAINT option of the VARIABLE command. This example illustrates constraints using labels defined for parameters in the MODEL command and labels defined using the NEW option. The NEW option is used to assign labels and starting values to parameters not in the analysis model. Parameters in the analysis model are given labels by placing a name in parentheses after the parameter in the MODEL command.
In the MODEL command, labels are defined for twelve parameters. The list function can be used when assigning labels to a list of parameters. The labels lam2, lam3, lam5, and lam6 are assigned to the factor loadings for y2, y3, y5, and y6. The labels vf1 and vf2 are assigned to the factor variances for f1 and f2. The labels ve1, ve2, ve3, ve4, ve5, and ve6 are assigned to the residual variances of y1, y2, y3, y4, y5, and y6.
In the MODEL CONSTRAINT command, the NEW option is used to assign labels to four parameters that are not in the analysis model: rel2, rel5, stan3, and stan6. The parameters rel2 and rel6 estimate the reliability of y2 and y6 where reliability is defined as variance explained divided by total variance. The parameters stan3 and stan6 estimate the standardized coefficients for y3 and y6 using conventional standardization formulas. In the statement that begins 0=, two parameters are held equal to each other by defining their difference as zero. In the last two statements, the residual variance of y2 is constrained to be greater than the residual variance of y5, and the residual variance of y4 is constrained to be greater than zero. The STANDARDIZED option of the OUTPUT command is requested to illustrate that the R-square values found in the output are the same as the estimated reliabilities, and the standardized values found in the output are the same as the estimated standardized values. Standard errors for parameters named using the NEW option are given. The default estimator for this type of analysis is maximum likelihood. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. An explanation of the other commands can be found in Example 5.1.
TITLE: this is an example of a two-group twin
model for continuous outcomes using parameter constraints
DATA: FILE = ex5.21.dat;
VARIABLE: NAMES = y1 y2 g;
GROUPING = g(1 = mz 2 = dz);
MODEL: [y1-y2] (1);
y1-y2 (var);
y1 WITH y2 (covmz);
MODEL dz: y1 WITH y2 (covdz);
MODEL CONSTRAINT:
NEW(a c e h);
var = a**2 + c**2 + e**2;
covmz = a**2 + c**2;
covdz = 0.5*a**2 + c**2;
h = a**2/(a**2 + c**2 + e**2);

In this example, the model shown in the picture above is estimated using parameter constraints. The model estimated is the same as the model in Example 5.18.
In the MODEL command, labels are defined for three parameters. The label var is assigned to the variances of y1 and y2. Because they are given the same label, these parameters are held equal. In the overall MODEL command, the label covmz is assigned to the covariance between y1 and y2 for the monozygotic twins. In the group-specific MODEL command, the label covdz is assigned to the covariance between y1 and y2 for the dizygotic twins.
In the MODEL CONSTRAINT command, the NEW option is used to assign labels to four parameters that are not in the analysis model: a, c, e, and h. The three parameters a, c, and e are used to decompose the variances and covariances of y1 and y2 into genetic and environmental components. The parameter h does not impose restrictions on the model parameters but is used to compute the heritability estimate and its standard error. The default estimator for this type of analysis is maximum likelihood. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. An explanation of the other commands can be found in Examples 5.1, 5.14, 5.18, and 5.20.
TITLE: this is an example of a two-group twin
model for categorical outcomes using parameter constraints
DATA: FILE = ex5.22.dat;
VARIABLE: NAMES = u1 u2 g;
GROUPING = g(1 = mz 2 = dz);
CATEGORICAL = u1 u2;
MODEL: [u1$1-u2$1](1);
u1 WITH u2(covmz);
MODEL dz: u1 WITH u2(covdz);
MODEL CONSTRAINT:
NEW(a c e h);
covmz = a**2 + c**2;
covdz = 0.5*a**2 + c**2;
e = 1 - (a**2 + c**2);
h = a**2/1;
The difference between this example and Example 5.21 is that the outcomes are binary or ordered categorical instead of continuous variables. Because of this, the outcomes have no freely estimated residual variances. The ACE variance and covariance restrictions are placed on normally-distributed latent response variables underlying the categorical outcomes which are also called liabilities. This model is referred to as the threshold model for liabilities (Neale & Cardon, 1992). The model estimated is the same as the model in Example 5.19.
The variance contribution from the E factor is not a freely estimated parameter with categorical outcomes. It is a remainder obtained by subtracting the variance contributions of the A and C factors from the unit variance of the latent response variables underlying u1 and u2 as shown in the MODEL CONSTRAINT command. The denominator for the heritability estimate is one with categorical outcomes because the latent response variables have unit variances.
The default estimator for this type of analysis is a robust weighted least squares estimator. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. With maximum likelihood, logistic or probit regressions are estimated using a numerical integration algorithm. Note that numerical integration becomes increasingly more computationally demanding as the number of factors and the sample size increase. An explanation of the other commands can be found in Examples 5.1, 5.14, 5.19 and 5.21.
TITLE: this is an example of a QTL sibling model for a continuous outcome using parameter constraints
DATA: FILE = ex5.23.dat;
VARIABLE: NAMES = y1 y2 pihat;
USEVARIABLES = y1 y2;
CONSTRAINT = pihat;
MODEL: [y1-y2] (1);
y1-y2 (var);
y1 WITH y2 (cov);
MODEL CONSTRAINT:
NEW(a e q);
var = a**2 + e**2 + q**2;
cov = 0.5*a**2 + pihat*q**2;
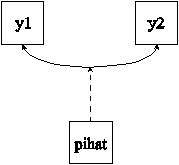
In this example, the model shown in the picture above is estimated. This is a QTL model for two siblings (Marlow et al. 2003; Posthuma et al. 2004) for continuous outcomes where parameter constraints are used to represent the A, E, and Q components. The A component represents the additive genetic effects which correlate 0.5 for siblings. The E component represents uncorrelated environmental effects. The Q component represents a quantitative trait locus (QTL). The observed variable pihat contains the estimated proportion alleles shared identity-by-descent (IBD) by the siblings and moderates the effect of the Q component on the covariance between the outcomes.
The CONSTRAINT option in the VARIABLE command is used to identify the variables that can be used in the MODEL CONSTRAINT command. These can be not only variables used in the MODEL command but also other variables. In this example, the variable pihat is used in the MODEL CONSTRAINT command although it is not used in the MODEL command.
In the MODEL command, the (1) following the first bracket statement specifies that the intercepts of y1 and y2 are held equal across the two siblings. In addition, labels are defined for two parameters. The label var is assigned to the variances of y1 and y2. Because they are given the same label, these parameters are held equal. The label cov is assigned to the covariance between y1 and y2.
In the MODEL CONSTRAINT command, the NEW option is used to assign labels to three parameters that are not in the analysis model: a, e, and q. The three parameters a, e, and q and the variable pihat are used to decompose the variances and covariances of y1 and y2 into genetic, environmental, and QTL components. The default estimator for this type of analysis is maximum likelihood. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. An explanation of the other commands can be found in Examples 5.1 and 5.20.
TITLE: this is an example of an EFA with covariates (MIMIC) with continuous factor indicators and direct effects
DATA: FILE IS ex5.24.dat;
VARIABLE: NAMES ARE y1-y8 x1 x2;
MODEL: f1-f2 BY y1-y8(*1);
f1-f2 ON x1-x2;
y1 ON x1;
y8 ON x2;
OUTPUT: TECH1;
In this example, the EFA with covariates (MIMIC) with continuous factor indicators and direct effects shown in the picture above is estimated. This is an exploratory structural equation model (ESEM; Asparouhov & Muthén, 2009a). The factors f1 and f2 are EFA factors which have the same factor indicators. Unlike CFA, no factor loadings are fixed at zero. Instead, the four restrictions on the factor loadings, factor variances, and factor covariances necessary for identification are imposed by rotating the factor loading matrix and fixing the factor residual variances at one.
In the MODEL command, the BY statement specifies that the factors f1 and f2 are measured by the continuous factor indicators y1 through y8. The label 1 following an asterisk (*) in parentheses following the BY statement is used to indicate that f1 and f2 are a set of EFA factors. When no rotation is specified using the ROTATION option of the ANALYSIS command, the default oblique GEOMIN rotation is used. The intercepts and residual variances of the factor indicators are estimated and the residuals are not correlated as the default. The residual variances of the factors are fixed at one as the default. The residuals of the factors are correlated under the default oblique GEOMIN rotation. The first ON statement describes the linear regressions of f1 and f2 on the covariates x1 and x2. The second and third ON statements describe the linear regressions of y1 on x1 and y8 on x2. These regressions represent direct effects used to test for measurement non-invariance.
The default estimator for this type of analysis is maximum likelihood. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. An explanation of the other commands can be found in Example 5.1.
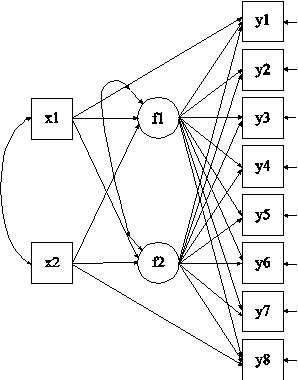
TITLE: this is an example of a SEM with EFA and CFA factors with continuous factor indicators
DATA: FILE IS ex5.25.dat;
VARIABLE: NAMES ARE y1-y12;
MODEL: f1-f2 BY y1-y6 (*1);
f3 BY y7-y9;
f4 BY y10-y12;
f3 ON f1-f2;
f4 ON f3;
In this example, the SEM with EFA and CFA factors with continuous factor indicators shown in the picture above is estimated. This is an exploratory structural equation model (ESEM; Asparouhov & Muthén, 2009a). The factors f1 and f2 are EFA factors which have the same factor indicators. Unlike CFA, no factor loadings are fixed at zero. Instead, the four restrictions on the factor loadings, factor variances, and factor covariances necessary for identification are imposed by rotating the factor loading matrix and fixing the factor variances at one. The factors f3 and f4 are CFA factors.
In the MODEL command, the first BY statement specifies that the factors f1 and f2 are measured by the continuous factor indicators y1 through y6. The label 1 following an asterisk (*) in parentheses following the BY statement is used to indicate that f1 and f2 are a set of EFA factors. When no rotation is specified using the ROTATION option of the ANALYSIS command, the default oblique GEOMIN rotation is used. For EFA factors, the intercepts and residual variances of the factor indicators are estimated and the residuals are not correlated as the default. The variances of the factors are fixed at one as the default. The factors are correlated under the default oblique GEOMIN rotation. The second BY statement specifies that f3 is measured by y7, y8, and y9. The third BY statement specifies that f4 is measured by y10, y11, and y12. The metric of the factors is set automatically by the program by fixing the first factor loading in each BY statement to 1. This option can be overridden. The intercepts and residual variances of the factor indicators are estimated and the residual are not correlated as the default. The residual variances of the factors are estimated as the default.
The first ON statement describes the linear regression of f3 on the set of EFA factors f1 and f2. The second ON statement describes the linear regression of f4 on f3. The default estimator for this type of analysis is maximum likelihood. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. An explanation of the other commands can be found in Example 5.1.
TITLE: this is an example of an EFA at two time points with factor loading invariance and correlated residuals across time
DATA: FILE IS ex5.26.dat;
VARIABLE: NAMES ARE y1-y12;
MODEL: f1-f2 BY y1-y6 (*t1 1);
f3-f4 BY y7-y12 (*t2 1);
y1-y6 PWITH y7-y12;
OUTPUT: TECH1 STANDARDIZED;
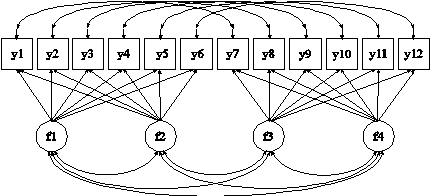
In this example, the EFA at two time points with factor loading invariance and correlated residuals across time shown in the picture above is estimated. This is an exploratory structural equation model (ESEM; Asparouhov & Muthén, 2009a). The factor indicators y1 through y6 and y7 through y12 are the same variables measured at two time points. The factors f1 and f2 are one set of EFA factors which have the same factor indicators and the factors f3 and f4 are a second set of EFA factors which have the same factor indicators. Unlike CFA, no factor loadings are fixed at zero in either set. Instead, for each set, the four restrictions on the factor loadings, factor variances, and factor covariances necessary for identification are imposed by rotating the factor loading matrix and fixing the factor variances at one at the first time point. For the other time point, factor variances are free to be estimated as the default when factor loadings are constrained to be equal across time.
In the MODEL command, the first BY statement specifies that the factors f1 and f2 are measured by the continuous factor indicators y1 through y6. The label t1 following an asterisk (*) in parentheses following the BY statement is used to indicate that f1 and f2 are a set of EFA factors. The second BY statement specifies that the factors f3 and f4 are measured by the continuous factor indicators y7 through y12. The label t2 following an asterisk (*) in parentheses following the BY statement is used to indicate that f3 and f4 are a set of EFA factors. The number 1 following the labels t1 and t2 specifies that the factor loadings matrices for the two sets of EFA factors are constrained to be equal. When no rotation is specified using the ROTATION option of the ANALYSIS command, the default oblique GEOMIN rotation is used.
For EFA factors, the intercepts and residual variances of the factor indicators are estimated and the residuals are not correlated as the default. The intercepts are not held equal across time as the default. The means of the factors are fixed at zero at both time points and the variances of the factors are fixed at one as the default. In this example because the factor loadings are constrained to be equal across time, the factor variances are fixed at one at the first time point and are free to be estimated at the other time point. The factors are correlated as the default under the oblique GEOMIN rotation. The PWITH statement specifies that the residuals for each factor indicator are correlated over time. The default estimator for this type of analysis is maximum likelihood. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. An explanation of the other commands can be found in Example 5.1.
TITLE: this is an example of multiple-group EFA with continuous factor indicators with no measurement invariance
DATA: FILE IS ex5.27.dat;
VARIABLE: NAMES ARE y1-y10 group;
GROUPING IS group (1 = g1 2 = g2);
MODEL: f1-f2 BY y1-y10 (*1);
[f1-f2@0];
MODEL g2: f1-f2 BY y1-y10 (*1);
[y1-y10];
OUTPUT: TECH1;

In this example, the multiple-group EFA with continuous indicators shown in the picture above is estimated. This is an exploratory structural equation model (ESEM; Asparouhov & Muthén, 2009a). The factors f1 and f2 are EFA factors which have the same factor indicators. Unlike CFA, no factor loadings are fixed at zero. Instead, for the first group the four restrictions on the factor loadings, factor variances, and factor covariances necessary for model identification are imposed by rotating the factor loading matrix and fixing the factor variances at one in all groups. The first model in this example imposes no equality constraints on the model parameters across the two groups. Four subsequent models impose varying degrees of invariance on the model parameters.
In the MODEL command, the BY statement specifies that the factors f1 and f2 are measured by the continuous factor indicators y1 through y10. The label 1 following an asterisk (*) in parentheses following the BY statement is used to indicate that f1 and f2 are a set of EFA factors. When no rotation is specified using the ROTATION option of the ANALYSIS command, the default oblique GEOMIN rotation is used.
The intercepts and residual variances of the factor indicators are estimated and the residuals are not correlated as the default. The variances of the factors are fixed at one in both groups. The factors are correlated under the default oblique GEOMIN rotation. The bracket statement specifies that the factor means are fixed at zero in both groups to override the default of the factor means being fixed at zero in the first group and being free in the other group.
In the group-specific MODEL command for g2, the BY statement relaxes the default equality constraint on the factor loading matrices in the two groups. The bracket statement relaxes the default equality constraint on the intercepts of the factor indicators y1 through y10 in the two groups. The default estimator for this type of analysis is maximum likelihood. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. An explanation of the other commands can be found in Example 5.1
Following is the second part of the example where equality of factor loading matrices across the two groups is imposed. The variances of the factors are fixed at one in the first group and are free to be estimated in the other group.
MODEL: f1-f2 BY y1-y10 (*1);
[f1-f2@0];
MODEL g2: [y1-y10];
Equality of factor loading matrices is accomplished by removing the BY statement from the group-specific MODEL command for g2. Equality of factor loading matrices is the default.
Following is the third part of the example where equality of factor loading matrices and intercepts of the factor indicators across the two groups is imposed.
MODEL: f1-f2 by y1-y10 (*1);
Equality of factor indicator intercepts is accomplished by removing the bracket statement for y1 through y10 from the group-specific MODEL command for g2. Equality of factor indicator intercepts is the default. This specification is the default setting in multiple group analysis, specifying measurement invariance of the intercepts of the factor indicators and the factor loading matrices. The factor means are fixed at zero in the first group and are free to be estimated in the other group as the default.
Following is the fourth part of the example where equality of factor variances and the factor covariance is imposed in addition to measurement invariance of the intercepts and factor loading matrices.
MODEL: f1-f2 by y1-y10 (*1);
f1 WITH f2 (1);
f1-f2@1;
In the MODEL command, the number one in parentheses following the WITH statement specifies that the covariance between f1 and f2 is held equal across the two groups. The default in multiple group EFA when factor loading matrices are held equal across groups is that the factor variances are fixed to one in the first group and are free to be estimated in the other group. The third statement in the MODEL command overrides this default by specifing that the factor variances are fixed at one in both groups.
Following is the fifth part of the example where in addition to equality of factor variances and the factor covariance, equality of the factor means is imposed in addition to measurement invariance of the intercepts and factor loading matrices.
MODEL: f1-f2 by y1-y10 (*1);
f1 WITH f2 (1);
f1-f2@1;
[f1-f2@0];
The default in multiple group EFA is that the factor means are fixed to zero in the first group and are free to be estimated in the other groups. The bracket statement in the MODEL command specifies that the factor means are fixed at zero in both groups.
TITLE: this is an example of an EFA with residual variances constrained to be greater than zero
DATA: FILE = ex5.28.dat;
VARIABLE: NAMES = y1-y10;
ANALYSIS: ROTATION = GEOMIN;
MODEL: f1-f2 BY y1-y10 (*1);
y1-y10 (v1-v10);
MODEL CONSTRAINT:
DO(1,10) v#>0;
OUTPUT: STDY;
In this example, an exploratory factor analysis with residual variances constrained to be greater than zero is carried out using a Geomin rotation. This is an exploratory structural equation model (ESEM; Asparouhov & Muthén, 2009a). The factors f1 and f2 are EFA factors which have the same factor indicators. By specifying GEOMIN, an EFA will be carried out using the Geomin rotation. The default is an oblique rotation. An orthogonal rotation can be obtained by specifying ROTATION=GEOMIN(ORTHOGONAL). The ROTATION option can be used to specify other rotations.
In the MODEL command, the BY statement specifies that the factors f1 and f2 are measured by the continuous factor indicators y1 through y10. The label 1 following an asterisk (*) in parentheses following the BY statement is used to indicate that f1 and f2 are a set of EFA factors. The intercepts and residual variances of the factor indicators are estimated and the residuals are not correlated as the default. The variances of the factors are fixed at one as the default. The DO option of the MODEL CONSTRAINT command is used to constrain the residual variances of the factor indicators to be greater than zero. The DO option provides a do loop to facilitate specifying the same expression for a set of parameters. The parameters are given labels in the MODEL command. In the DO option, the numbers in parentheses give the range of values for the do loop. The number sign (#) is replaced by these values during the execution of the do loop. In the OUTPUT command, the STDY option is chosen for standardization with respect to y. This puts the results in the metric of an EFA. The default estimator for this type of analysis is maximum likelihood. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. An explanation of the other commands can be found in Examples 5.1.
TITLE: this is an example of a bi-factor EFA using ESEM
DATA: FILE = ex5.29.dat;
VARIABLE: NAMES = y1-y10;
ANALYSIS: ROTATION = BI-GEOMIN;
MODEL: fg f1 f2 BY y1-y10 (*1);
OUTPUT: STDY;
In this example, a bi-factor exploratory factor analysis (Jennrich & Bentler, 2011, 2012) using ESEM with continuous factor indicators is carried out using a bi-factor Geomin rotation. This is an exploratory structural equation model (ESEM; Asparouhov & Muthén, 2009a). The factors fg, f1, and f2 are EFA factors which have the same factor indicators. By specifying BI-GEOMIN, a bi-factor EFA will be carried out using a bi-factor Geomin rotation. The default is an oblique solution where the specific factors are correlated with the general factor and are correlated with each other. In the orthogonal solution, the specific factors are uncorrelated with the general factor and are uncorrelated with each other. An orthogonal rotation is obtained by specifying ROTATION=BI-GEOMIN(ORTHOGONAL). An alternative bi-factor rotation can be obtained using the BI-CF-QUARTIMAX setting of the ROTATION option.
In the MODEL command, the BY statement specifies that the factors fg, f1, and f2 are measured by the continuous factor indicators y1 through y10. The factor fg is a general factor and f1 and f2 are specific factors. The label 1 following an asterisk (*) in parentheses following the BY statement is used to indicate that fg, f1, and f2 are a set of EFA factors. The intercepts and residual variances of the factor indicators are estimated and the residuals are not correlated as the default. The variances of the factors are fixed at one as the default. In the OUTPUT command, the STDY option is chosen for standardization with respect to y. This puts the results in the metric of an EFA. The default estimator for this type of analysis is maximum likelihood. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. An explanation of the other commands can be found in Example 5.1.
TITLE: this is an example of bi-factor EFA with
two items loading on only the general
factor
DATA: FILE = ex5.30.dat;
VARIABLE: NAMES = y1-y10;
ANALYSIS: ROTATION = GEOMIN;
MODEL: fg BY y1-y10*;
fg@1;
f1-f2 BY y1-y8 (*1);
fg WITH f1-f2@0;
OUTPUT: STDY;
In this example, a bi-factor exploratory factor analysis with continuous factor indicators is carried out using a Geomin rotation. This is an exploratory structural equation model (ESEM; Asparouhov & Muthén, 2009a). The general factor fg is a CFA factor. The specific factors f1 and f2 are EFA factors which have the same factor indicators. Only the specific factors are rotated. By specifying GEOMIN, an EFA will be carried out using the Geomin rotation for the specific factors. The default is an oblique rotation. An orthogonal rotation can be obtained by specifying ROTATION=GEOMIN(ORTHOGONAL). The ROTATION option can be used to specify other rotations.
In the MODEL command, the first BY statement specifies that the general factor fg is measured by y1 through y10. The asterisk (*) frees the first factor loading which is fixed at one as the default to define the metric of the factor. Instead the metric of the factor is defined by fixing the factor variance at one. The second BY statement specifies that the specific factors f1 and f2 are measured by the continuous factor indicators y1 through y8. The label following an asterisk (*) in parentheses following the BY statement is used to indicate that f1 and f2 are a set of EFA factors. The variances of the factors are fixed at one as the default. The specific factors are correlated under the oblique Geomin rotation. The WITH statement specifies that the general and specific factors are not correlated. The intercepts and residual variances of the factor indicators are estimated and the residuals are not correlated as the default. In the OUTPUT command, the STDY option is chosen for standardization with respect to y. This puts the results in the metric of an EFA. The default estimator for this type of analysis is maximum likelihood. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. An explanation of the other commands can be found in Example 5.1.
TITLE: this is an example of a Bayesian bi-factor CFA with two items loading on only the general factor and cross-loadings with zero-mean and small-variance priors
DATA: FILE = ex5.31.dat;
VARIABLE: NAMES = y1-y10;
ANALYSIS: ESTIMATOR = BAYES;
PROCESSORS = 2;
MODEL: fg BY y1-y10*;
fg@1;
f1 BY y1-y4
y5-y10 (f1xlam5-f1xlam10);
f2 BY y5-y8
y1-y4 y9-y10(f2xlam1-f2xlam6);
fg WITH f1-f2@0;
MODEL PRIORS:
f1xlam5-f2xlam6~N(0,0.01);
PLOT: TYPE = PLOT2;
In this example, a bi-factor CFA with two items loading on only the general factor and cross-loadings with zero-mean and small-variance priors is carried out using the Bayes estimator. This is a Bayesian structural equation model (BSEM; Muthén & Asparouhov, 2012). By specifying ESTIMATOR=BAYES, a Bayesian analysis will be carried out. In Bayesian estimation, the default is to use two independent Markov chain Monte Carlo (MCMC) chains. If multiple processors are available, using PROCESSORS=2 will speed up computations.
In the MODEL command, the first BY statement specifies that the general factor, fg, is measured by the continuous factor indicators y1 through y10. The asterisk (*) frees the first factor loading which is fixed at one as the default to define the metric of the factor. Instead the metric of the factor is defined by fixing the factor variance at one. The second and third BY statements specify that the specific factors, f1 and f2, are measured by y1 through y10. The first factor loadings are fixed at one to set the metric of the factors. The first line of each BY statement shows the major loadings for each factor. The second line shows the cross-loadings which are assigned labels. For f1, labels are assigned to cross-loadings for y5 through y10. For f2, labels are assigned to cross-loadings for y1 through y4, y9, and y10. The WITH statement specifies that the general and specific factors are not correlated. The intercepts and residual variances of the factor indicators are estimated and the residuals are not correlated as the default. In MODEL PRIORS, the labels assigned in the MODEL command are used to assign zero-mean and small-variance priors to the cross-loadings. By specifying TYPE=PLOT2 in the PLOT command, the following plots are available: posterior parameter distributions, posterior parameter trace plots, autocorrelation plots, posterior predictive checking scatterplots, and posterior predictive checking distribution plots. An explanation of the other commands can be found in Example 5.1.
TITLE: this is an example of a Bayesian MIMIC model with cross-loadings and direct effects with zero-mean and small-variance priors
DATA: FILE = ex5.32.dat;
VARIABLE: NAMES = y1-y6 x1-x3;
ANALYSIS: ESTIMATOR = BAYES;
PROCESSORS = 2;
MODEL: f1 BY y1-y3
y4-y6 (xload4-xload6);
f2 BY y4-y6
y1-y3 (xload1-xload3);
f1-f2 ON x1-x3;
y1-y6 ON x1-x3 (dir1-dir18);
MODEL PRIORS:
xload1-xload6~N(0,0.01);
dir1-dir18~N(0,0.01);
PLOT: TYPE = PLOT2;
In this example, a MIMIC model with cross-loadings and direct effects with zero-mean and small-variance priors is carried out using the Bayes estimator. This is a Bayesian structural equation model (BSEM; Muthén & Asparouhov, 2012).
In the MODEL command, the first BY statement specifies that f1 is measured by the continuous factor indicators y1 through y6. The second BY statements specifies that f2 is measured by the continuous factor indicators y1 through y6. The first factor loadings are fixed at one to set the metric of the factors. The first line of each BY statement shows the major loadings for each factor. The second line shows the cross-loadings which are assigned labels. For f1, labels are assigned to y4 through y6. For f2, labels are assigned to y1 through y3. The intercepts and residual variances of the factor indicators are estimated and the residuals are not correlated as the default. In MODEL PRIORS, the labels assigned in the MODEL command are used to assign zero-mean and small-variance priors to the factor loadings. The first ON statement describes the linear regressions of f1 and f2 on the covariates x1, x2, and x3. The residual variances of f1 and f2 are estimated and the residuals are correlated as the default. The second ON statement describes the linear regressions of y1 through y6 on the covariates x1, x2, and x3. These are direct effects which are assumed to be small. Labels are assigned to these regression coefficients. In MODEL PRIORS, the labels assigned in the MODEL command are used to assign zero-mean and small-variance priors to the factor loadings and regression coefficients. By specifying TYPE=PLOT2 in the PLOT command, the following plots are available: posterior parameter distributions, posterior parameter trace plots, autocorrelation plots, posterior predictive checking scatterplots, and posterior predictive checking distribution plots. An explanation of the other commands can be found in Examples 5.1 and 5.31.
TITLE: this is an example of a Bayesian
multiple group model with approximate
measurement invariance using zero-mean and small-variance priors
DATA: FILE = ex5.33.dat;
VARIABLE: NAMES = u y1-y6 group;
USEVARIABLES = y1-y6 group;
CLASSES = c(10);
KNOWNCLASS = c(group = 1-10);
ANALYSIS: TYPE = MIXTURE;
ESTIMATOR = BAYES;
PROCESSORS = 2;
MODEL = ALLFREE;
MODEL: %OVERALL%
f1 BY y1-y3* (lam#_1-lam#_3);
f2 BY y4-y6* (lam#_4-lam#_6);
[y1-y6] (nu#_1-nu#_6);
%c#10%
f1-f2@1;
[f1-f2@0];
MODEL PRIORS:
DO(1,6) DIFF(lam1_#-lam10_#)~N(0,0.01);
DO(1,6) DIFF(nu1_#-nu10_#)~N(0,0.01);
PLOT: TYPE = PLOT2;
OUTPUT: TECH1 TECH8;
In this example, a multiple group model with approximate measurement invariance using zero-mean and small-variance priors is carried out using the Bayes estimator. This is a Bayesian structural equation model (BSEM; Muthén & Asparouhov, 2012). In Bayesian estimation, multiple group analysis is carried out using the CLASSES and KNOWNCLASS options and TYPE=MIXTURE. The CLASSES option is used to assign names to the categorical latent variables in the model and to specify the number of latent classes in the model for each categorical latent variable. In the example above, there is one categorical latent variable c that has ten latent classes. The KNOWNCLASS option identifies c as the categorical latent variable for which latent class membership is known. The information in parentheses following the categorical latent variable name defines the known classes using an observed variable. In this example, the observed variable group is used to define the known classes. The first class consists of individuals with the value 1 on the variable group. The second class consists of individuals with the value 2 on the variable group etc.
MODEL=ALLFREE is used with TYPE=MIXTURE, the KNOWNCLASS option, ESTIMATOR=BAYES, and a special labeling function to assign zero-mean and small-variance priors to differences in intercepts, thresholds, and factor loadings across groups. By specifying MODEL=ALLFREE, factor means, variances, and covariances are free across groups except for factor means in the last group which are fixed at zero. In addition, intercepts, thresholds, factor loadings, and residual variances of the factor indicators are free across the groups.
In the overall model, the first BY statement specifies that f1 is measured by the continuous factor indicators y1 through y3. The second BY statement specifies that f2 is measured by the continuous factor indicators y4 through y6. In both BY statements the asterisk (*) frees the first factor loadings which are fixed at one as the default to set the metric of the factors. The metric of the factors is set instead by fixing the factor variances to one in class 10. The residual variances of the factor indicators are estimated and the residuals are not correlated as the default.
In the overall part of the model, labels are assigned to the factor loadings and the intercepts using automatic labeling for groups. The labels must include the number sign (#) followed by the underscore (_) symbol followed by a number. The number sign (#) refers to a group and the number refers to a parameter. The label lam#_1 is assigned to the factor loading for y1; the label lam#_2 is assigned to the factor loading for y2; and the label lam#_3 is assigned to the factor loading for y3. These labels are expanded to include group information. For example, the label for parameter 1 is expanded across the ten groups to give labels lam1_1, lam2_1 through lam10_1. In MODEL PRIORS, these expanded labels are used to assign zero-mean and small-variance priors to the differences across groups of the factor loadings and intercepts using the DO and DIFFERENCE options. They can be used together to simplify the assignment of priors to a large set of difference parameters for models with multiple groups and multiple time points. For the DO option, the numbers in parentheses give the range of values for the do loop. The number sign (#) is replaced by these values during the execution of the do loop. The numbers refer to the six factor indicators.
By specifying TYPE=PLOT2 in the PLOT command, the following plots are available: posterior parameter distributions, posterior parameter trace plots, autocorrelation plots, posterior predictive checking scatterplots, and posterior predictive checking distribution plots. An explanation of the other commands can be found in Example 5.1 and 5.31.