This chapter describes the user language of MODELING

EXAMPLES: MULTILEVEL MODELING WITH COMPLEX SURVEY DATA

Complex survey data refers to data obtained by stratification, cluster sampling and/or sampling with an unequal probability of selection. Complex survey data are also referred to as multilevel or hierarchical data. For an overview, see Muthén and Satorra (1995). There are two approaches to the analysis of complex survey data in Mplus.

One approach is to compute standard errors and a chi-square test of model fit taking into account stratification, non-independence of observations due to cluster sampling, and/or unequal probability of selection. Subpopulation analysis is also available. With sampling weights, parameters are estimated by maximizing a weighted loglikelihood function. Standard error computations use a sandwich estimator. This approach can be obtained by specifying TYPE=COMPLEX in the ANALYSIS command in conjunction with the STRATIFICATION, CLUSTER, WEIGHT, and/or SUBPOPULATION options of the VARIABLE command. Observed outcome variables can be continuous, censored, binary, ordered categorical (ordinal), unordered categorical (nominal), counts, or combinations of these variable types. The implementation of these methods in Mplus is discussed in Asparouhov (2005, 2006) and Asparouhov and Muthén (2005, 2006a).

A second approach is to specify a model for each level of the multilevel data thereby modeling the non-independence of observations due to cluster sampling. This is commonly referred to as multilevel modeling. The use of sampling weights in the estimation of parameters, standard errors, and the chi-square test of model fit is allowed. Both individual-level and cluster-level weights can be used. With sampling weights, parameters are estimated by maximizing a weighted loglikelihood function. Standard error computations use a sandwich estimator. This approach can be obtained for two-level data by specifying TYPE=TWOLEVEL in the ANALYSIS command in conjunction with the CLUSTER, WEIGHT, WTSCALE, BWEIGHT, and/or BWTSCALE options of the VARIABLE command. For TYPE=TWOLEVEL, observed outcome variables can be continuous, censored, binary, ordered categorical (ordinal), unordered categorical (nominal), counts, or combinations of these variable types. This approach can also be obtained for three-level data by specifying TYPE=THREELEVEL in conjunction with the CLUSTER, WEIGHT, WTSCALE, B2WEIGHT, B3WEIGHT and/or BWTSCALE options of the VARIABLE command. For TYPE=THREELEVEL, observed outcome variables can be continuous. Complex survey features are not available for TYPE=THREELEVEL with categorical variables or TYPE=CROSSCLASSIFIED because these models are estimated using Bayesian analysis for which complex survey features have not been generally developed.

The approaches described above can be combined by specifying TYPE=COMPLEX TWOLEVEL in the ANALYSIS command in conjunction with the STRATIFICATION, CLUSTER, WEIGHT, WTSCALE, BWEIGHT, and/or BWTSCALE options of the VARIABLE command or TYPE=COMPLEX THREELEVEL in conjunction with the STRATIFICATION, CLUSTER, WEIGHT, WTSCALE, B2WEIGHT, B3WEIGHT, and/or BWTSCALE options of the VARIABLE command For TYPE=TWOLEVEL, when there is clustering due to two cluster variables, the standard errors and chi-square test of model fit are computed taking into account the clustering due to the highest cluster level using TYPE=COMPLEX whereas clustering due to the lowest cluster level is modeled using TYPE=TWOLEVEL. For TYPE=THREELEVEL, when there is clustering due to three cluster variables, the standard errors and chi-square test of model fit are computed taking into account the clustering due to the highest cluster level using TYPE=COMPLEX whereas clustering due to the other cluster levels is modeled using TYPE=THREELEVEL.

A distinction can be made between cross-sectional data in which non-independence arises because of cluster sampling and longitudinal data in which non-independence arises because of repeated measures of the same individuals across time. With cross-sectional data, the number of levels in Mplus is the same as the number of levels in conventional multilevel modeling programs. Mplus allows three-level modeling. With longitudinal data, the number of levels in Mplus is one less than the number of levels in conventional multilevel modeling programs because Mplus takes a multivariate approach to repeated measures analysis. Longitudinal models are two-level models in conventional multilevel programs, whereas they are single-level models in Mplus. These models are discussed in Chapter 6. Three-level analysis where time is the first level, individual is the second level, and cluster is the third level is handled by two-level modeling in Mplus (see also Muthén, 1997). Four-level analysis where time is the first level, individual is the second level, classroom is the third level, and school is the fourth level is handled by three-level modeling in Mplus.

Time series analysis is used to analyze intensive longitudinal data such as those obtained with ecological momentary assessments, experience sampling methods, daily diary methods, and ambulatory assessments. Such data typically have a large number of time points, for example, twenty to two hundred. The measurements are typically closely spaced in time. In Mplus, a variety of two-level and cross-classified time series models can be estimated. These include univariate autoregressive, regression, cross-lagged, confirmatory factor analysis, Item Response Theory, and structural equation models for continuous, binary, ordered categorical (ordinal), or combinations of these variable types. N=1 versions of these models can be found in Chapter 6.

The general latent variable modeling framework of Mplus allows the integration of random effects and other continuous latent variables within a single analysis model. Random effects are allowed for both independent and dependent variables and both observed and latent variables. Random effects representing across-cluster variation in intercepts and slopes or individual differences in growth can be combined with factors measured by multiple indicators on both the individual and cluster levels. Random factor loadings are available as a special case of random slopes. Random variances are also available. In line with SEM, regressions among random effects, among factors, and between random effects and factors are allowed.

Multilevel models can include regression analysis, path analysis, confirmatory factor analysis (CFA), item response theory (IRT) analysis, structural equation modeling (SEM), latent class analysis (LCA), latent transition analysis (LTA), latent class growth analysis (LCGA), growth mixture modeling (GMM), discrete-time survival analysis, continuous-time survival analysis, and combinations of these models.

For TYPE=TWOLEVEL, there are four estimator options. The first estimator option is full-information maximum likelihood which allows continuous, censored, binary, ordered categorical (ordinal), unordered categorical (nominal), counts, or combinations of these variable types; random intercepts and slopes; and missing data. With longitudinal data, maximum likelihood estimation allows modeling of individually-varying times of observation and random slopes for time-varying covariates. Non-normality robust standard errors and a chi-square test of model fit are available. The second estimator option is limited-information weighted least squares (Asparouhov & Muthén, 2007) which allows continuous, binary, ordered categorical (ordinal), and combinations of these variables types; random intercepts; and missing data. The third estimator option is the Muthén limited information estimator (MUML; Muthén, 1994) which is restricted to models with continuous variables, random intercepts, and no missing data. The fourth estimator option is Bayes which allows continuous, categorical, and combinations of these variable types; random intercepts and slopes; and missing data.

All two-level models can be estimated using the following special features:

· Multiple group analysis

· Missing data

· Complex survey data

· Latent variable interactions and non-linear factor analysis using maximum likelihood

· Random slopes

· Individually-varying times of observations

· Linear and non-linear parameter constraints

· Indirect effects including specific paths

· Maximum likelihood estimation for all outcome types

· Wald chi-square test of parameter equalities

For continuous, censored with weighted least squares estimation, binary, and ordered categorical (ordinal) outcomes, multiple group analysis is specified by using the GROUPING option of the VARIABLE command for individual data. For censored with maximum likelihood estimation, unordered categorical (nominal), and count outcomes, multiple group analysis is specified using the KNOWNCLASS option of the VARIABLE command in conjunction with the TYPE=MIXTURE option of the ANALYSIS command. The default is to estimate the model under missing data theory using all available data. The LISTWISE option of the DATA command can be used to delete all observations from the analysis that have missing values on one or more of the analysis variables. Corrections to the standard errors and chi-square test of model fit that take into account stratification, non-independence of observations, and unequal probability of selection are obtained by using the TYPE=COMPLEX option of the ANALYSIS command in conjunction with the STRATIFICATION, CLUSTER, and WEIGHT options of the VARIABLE command. Latent variable interactions are specified by using the | symbol of the MODEL command in conjunction with the XWITH option of the MODEL command. Random slopes are specified by using the | symbol of the MODEL command in conjunction with the ON option of the MODEL command. Individually-varying times of observations are specified by using the | symbol of the MODEL command in conjunction with the AT option of the MODEL command and the TSCORES option of the VARIABLE command. Linear and non-linear parameter constraints are specified by using the MODEL CONSTRAINT command. Indirect effects are specified by using the MODEL INDIRECT command. Maximum likelihood estimation is specified by using the ESTIMATOR option of the ANALYSIS command. The MODEL TEST command is used to test linear restrictions on the parameters in the MODEL and MODEL CONSTRAINT commands using the Wald chi-square test.

For TYPE=THREELEVEL, there are two estimator options. The first estimator option is full-information maximum likelihood which allows continuous variables; random intercepts and slopes; and missing data. Non-normality robust standard errors and a chi-square test of model fit are available. The second estimator option is Bayes which allows continuous, categorical, and combinations of these variable types; random intercepts and slopes; and missing data.

All three-level models can be estimated using the following special features:

· Multiple group analysis

· Missing data

· Complex survey data

· Random slopes

· Linear and non-linear parameter constraints

· Maximum likelihood estimation for all outcome types

· Wald chi-square test of parameter equalities

For continuous outcomes, multiple group analysis is specified by using the GROUPING option of the VARIABLE command. The default is to estimate the model under missing data theory using all available data. The LISTWISE option of the DATA command can be used to delete all observations from the analysis that have missing values on one or more of the analysis variables. Corrections to the standard errors and chi-square test of model fit that take into account stratification, non-independence of observations, and unequal probability of selection are obtained by using the TYPE=COMPLEX option of the ANALYSIS command in conjunction with the STRATIFICATION, CLUSTER, and WEIGHT options of the VARIABLE command. Random slopes are specified by using the | symbol of the MODEL command in conjunction with the ON option of the MODEL command. Linear and non-linear parameter constraints are specified by using the MODEL CONSTRAINT command. Maximum likelihood estimation is specified by using the ESTIMATOR option of the ANALYSIS command. The MODEL TEST command is used to test linear restrictions on the parameters in the MODEL and MODEL CONSTRAINT commands using the Wald chi-square test.

For TYPE=CROSSCLASSIFIED, there is one estimator option, Bayes, which allows continuous, categorical, and combinations of these variable types; random intercepts and slopes; and missing data.

All cross-classified models can be estimated using the following special features:

· Missing data

· Random slopes

· Random factor loadings

· Random variances

The default is to estimate the model under missing data theory using all available data. The LISTWISE option of the DATA command can be used to delete all observations from the analysis that have missing values on one or more of the analysis variables. Random slopes are specified by using the | symbol of the MODEL command in conjunction with the ON option of the MODEL command.

Graphical displays of observed data and analysis results can be obtained using the PLOT command in conjunction with a post-processing graphics module. The PLOT command provides histograms, scatterplots, plots of individual observed and estimated values, and plots of sample and estimated means and proportions/probabilities. These are available for the total sample, by group, by class, and adjusted for covariates. The PLOT command includes a display showing a set of descriptive statistics for each variable. The graphical displays can be edited and exported as a DIB, EMF, or JPEG file. In addition, the data for each graphical display can be saved in an external file for use by another graphics program.

Following is the set of cross-sectional two-level modeling examples included in this chapter:

· 9.1: Two-level regression analysis for a continuous dependent variable with a random intercept

· 9.2: Two-level regression analysis for a continuous dependent variable with a random slope

· 9.3: Two-level path analysis with a continuous and a categorical dependent variable*

· 9.4: Two-level path analysis with a continuous, a categorical, and a cluster-level observed dependent variable

· 9.5: Two-level path analysis with continuous dependent variables and random slopes*

· 9.6: Two-level CFA with continuous factor indicators and covariates

· 9.7: Two-level CFA with categorical factor indicators and covariates*

· 9.8: Two-level CFA with continuous factor indicators, covariates, and random slopes

· 9.9: Two-level SEM with categorical factor indicators on the within level and cluster-level continuous observed and random intercept factor indicators on the between level

· 9.10: Two-level SEM with continuous factor indicators and a random slope for a factor*

· 9.11: Two-level multiple group CFA with continuous factor indicators

Following is the set of longitudinal two-level modeling examples included in this chapter:

· 9.12: Two-level growth model for a continuous outcome (three-level analysis)

· 9.13: Two-level growth model for a categorical outcome (three-level analysis)*

· 9.14: Two-level growth model for a continuous outcome (three-level analysis) with variation on both the within and between levels for a random slope of a time-varying covariate*

· 9.15: Two-level multiple indicator growth model with categorical outcomes (three-level analysis)

· 9.16: Linear growth model for a continuous outcome with time-invariant and time-varying covariates carried out as a two-level growth model using the DATA WIDETOLONG command

· 9.17: Two-level growth model for a count outcome using a zero-inflated Poisson model (three-level analysis)*

· 9.18: Two-level continuous-time survival analysis using Cox regression with a random intercept

· 9.19: Two-level mimic model with continuous factor indicators, random factor loadings, two covariates on within, and one covariate on between with equal loadings across levels

Following is the set of three-level and cross-classified modeling examples included in this chapter:

· 9.20: Three-level regression for a continuous dependent variable

· 9.21: Three-level path analysis with a continuous and a categorical dependent variable

· 9.22: Three-level MIMIC model with continuous factor indicators, two covariates on within, one covariate on between level 2, one covariate on between level 3 with random slopes on both within and between level 2

· 9.23: Three-level growth model with a continuous outcome and one covariate on each of the three levels

· 9.24: Regression for a continuous dependent variable using cross-classified data

· 9.25: Path analysis with continuous dependent variables using cross-classified data

· 9.26: IRT with random binary items using cross-classified data

· 9.27: Multiple indicator growth model with random intercepts and factor loadings using cross-classified data

Following is the set of cross-sectional two-level modeling examples with random residual variances included in this chapter:

· 9.28: Two-level regression analysis for a continuous dependent variable with a random intercept and a random residual variance

· 9.29: Two-level confirmatory factor analysis (CFA) with continuous factor indicators, covariates, and a factor with a random residual variance

Following is the set of two-level time series analysis examples with random effects included in this chapter:

· 9.30: Two-level time series analysis with a univariate first-order autoregressive AR(1) model for a continuous dependent variable with a random intercept, random AR(1) slope, and random residual variance

· 9.31: Two-level time series analysis with a univariate first-order autoregressive AR(1) model for a continuous dependent variable with a covariate, random intercept, random AR(1) slope, random slope, and random residual variance

· 9.32: Two-level time series analysis with a bivariate cross-lagged model for continuous dependent variables with random intercepts and random slopes

· 9.33: Two-level time series analysis with a first-order autoregressive AR(1) factor analysis model for a single continuous indicator and measurement error

· 9.34: Two-level time series analysis with a first-order autoregressive AR(1) confirmatory factor analysis (CFA) model for continuous factor indicators with random intercepts, a random AR(1) slope, and a random residual variance

· 9.35: Two-level time series analysis with a first-order autoregressive AR(1) IRT model for binary factor indicators with random thresholds, a random AR(1) slope, and a random residual variance

· 9.36: Two-level time series analysis with a bivariate cross-lagged model for two factors and continuous factor indicators with random intercepts and random slopes

· 9.37: Two-level time series analysis with a univariate first-order autoregressive AR(1) model for a continuous dependent variable with a covariate, linear trend, random slopes, and a random residual variance

Following is the set of cross-classified time series analysis examples with random effects included in this chapter:

· 9.38: Cross-classified time series analysis with a univariate first-order autoregressive AR(1) model for a continuous dependent variable with a covariate, random intercept, and random slope

· 9.39: Cross-classified time series analysis with a univariate first-order autoregressive AR(1) model for a continuous dependent variable with a covariate, linear trend, and random slope

· 9.40: Cross-classified time series analysis with a first-order autoregressive AR(1) confirmatory factor analysis (CFA) model for continuous factor indicators with random intercepts and a factor varying across both subjects and time

* Example uses numerical integration in the estimation of the model. This can be computationally demanding depending on the size of the problem.

EXAMPLE 9.1: TWO-LEVEL REGRESSION ANALYSIS FOR A CONTINUOUS DEPENDENT VARIABLE WITH A RANDOM INTERCEPT

TITLE: this is an example of a two-level

regression analysis for a continuous

dependent variable with a random intercept and an observed covariate

DATA: FILE = ex9.1a.dat;

VARIABLE: NAMES = y x w xm clus;

WITHIN = x;

BETWEEN = w xm;

CLUSTER = clus;

DEFINE: CENTER x (GRANDMEAN);

ANALYSIS: TYPE = TWOLEVEL;

MODEL:

%WITHIN%

y ON x;

%BETWEEN%

y ON w xm;

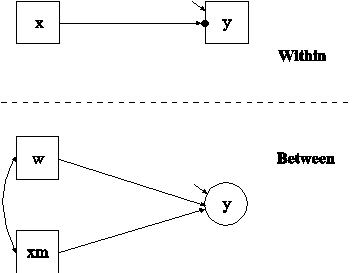
In this example, the two-level regression model shown in the picture above is estimated. The dependent variable y in this regression is continuous. Two ways of treating the covariate x are described. In this part of the example, the covariate x is treated as an observed variable in line with conventional multilevel regression modeling. In the second part of the example, the covariate x is decomposed into two latent variable parts.

The within part of the model describes the regression of y on an observed covariate x where the intercept is a random effect that varies across the clusters. In the within part of the model, the filled circle at the end of the arrow from x to y represents a random intercept that is referred to as y in the between part of the model. In the between part of the model, the random intercept is shown in a circle because it is a continuous latent variable that varies across clusters. The between part of the model describes the linear regression of the random intercept y on observed cluster-level covariates w and xm. The observed cluster-level covariate xm takes the value of the mean of x for each cluster. The within and between parts of the model correspond to level 1 and level 2 of a conventional multilevel regression model with a random intercept.

TITLE: this is an example of a two-level

regression analysis for a continuous

dependent variable with a random intercept and an observed covariate

The TITLE command is used to provide a title for the analysis. The title is printed in the output just before the Summary of Analysis.

DATA: FILE = ex9.1a.dat;

The DATA command is used to provide information about the data set to be analyzed. The FILE option is used to specify the name of the file that contains the data to be analyzed, ex9.1a.dat. Because the data set is in free format, the default, a FORMAT statement is not required.

VARIABLE: NAMES = y x w xm clus;

WITHIN = x;

BETWEEN = w xm;

CLUSTER = clus;

The VARIABLE command is used to provide information about the variables in the data set to be analyzed. The NAMES option is used to assign names to the variables in the data set. The data set in this example contains five variables: y, x, w, xm, and clus.

The WITHIN option is used to identify the variables in the data set that are measured on the individual level and modeled only on the within level. They are specified to have no variance in the between part of the model. The BETWEEN option is used to identify the variables in the data set that are measured on the cluster level and modeled only on the between level. Variables not mentioned on the WITHIN or the BETWEEN statements are measured on the individual level and can be modeled on both the within and between levels. Because y is not mentioned on the WITHIN statement, it is modeled on both the within and between levels. On the between level, it is a random intercept. The CLUSTER option is used to identify the variable that contains clustering information. The CENTER option is used to specify the type of centering to be used in an analysis and the variables that are to be centered. In this example, grand-mean centering is chosen.

DEFINE: CENTER x (GRANDMEAN);

The DEFINE command is used to transform existing variables and create new variables. The CENTER option is used to specify the type of centering to be used in an analysis and the variables that will be centered. Centering facilitates the interpretation of the results. In this example, the covariate is centered using the grand mean, that is, the sample mean of x is subtracted from the values of the covariate x.

ANALYSIS: TYPE = TWOLEVEL;

The ANALYSIS command is used to describe the technical details of the analysis. By selecting TWOLEVEL, a multilevel model with random intercepts will be estimated.

MODEL:

%WITHIN%

y ON x;

%BETWEEN%

y ON w xm;

The MODEL command is used to describe the model to be estimated. In multilevel models, a model is specified for both the within and between parts of the model. In the within part of the model, the ON statement describes the linear regression of y on the observed individual-level covariate x. The within-level residual variance in the regression of y on x is estimated as the default.

In the between part of the model, the ON statement describes the linear regression of the random intercept y on the observed cluster-level covariates w and xm. The intercept and residual variance of y are estimated as the default. The default estimator for this type of analysis is maximum likelihood with robust standard errors. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator.

Following is the second part of the example where the covariate x is decomposed into two latent variable parts.

TITLE: this is an example of a two-level

regression analysis for a continuous

dependent variable with a random intercept and a latent covariate

DATA: FILE = ex9.1b.dat;

VARIABLE: NAMES = y x w clus;

BETWEEN = w;

CLUSTER = clus;

DEFINE: CENTER = x (GRANDMEAN);

ANALYSIS: TYPE = TWOLEVEL;

MODEL:

%WITHIN%

y ON x (gamma10);

%BETWEEN%

y ON w

x (gamma01);

MODEL CONSTRAINT:

NEW(betac);

betac = gamma01 - gamma10;

The difference between this part of the example and the first part is that the covariate x is decomposed into two latent variable parts instead of being treated as an observed variable as in conventional multilevel regression modeling. The decomposition occurs when the covariate x is not mentioned on the WITHIN statement and is therefore modeled on both the within and between levels. When a covariate is not mentioned on the WITHIN statement, it is decomposed into two uncorrelated latent variables,

x_ij = x_wij + x_bj,

where i represents individual, j represents cluster, x_wij is the latent variable covariate used on the within level, and x_bj is the latent variable covariate used on the between level. This model is described in Muthén (1989, 1990, 1994). The latent variable covariate x_b is not used in conventional multilevel analysis. Using a latent covariate may, however, be advantageous when the observed cluster-mean covariate xm does not have sufficient reliability resulting in biased estimation of the between-level slope (Asparouhov & Muthén, 2006b; Ludtke et al., 2008).

The decomposition can be expressed as,

x_wij= x_ij- x_bj,

which can be viewed as an implicit, latent group-mean centering of the latent within-level covariate. To obtain results that are not group-mean centered, a linear transformation of the within and between slopes can be done as described below using the MODEL CONSTRAINT command.

In the MODEL command, the label gamma10 in the within part of the model and the label gamma01 in the between part of the model are assigned to the regression coefficients in the linear regression of y on x in both parts of the model for use in the MODEL CONSTRAINT command. The MODEL CONSTRAINT command is used to define linear and non-linear constraints on the parameters in the model. In the MODEL CONSTRAINT command, the NEW option is used to introduce a new parameter that is not part of the MODEL command. This parameter is called betac and is defined as the difference between gamma01 and gamma10. It corresponds to a “contextual effect” as described in Raudenbush and Bryk (2002, p. 140, Table 5.11).

EXAMPLE 9.2: TWO-LEVEL REGRESSION ANALYSIS FOR A CONTINUOUS DEPENDENT VARIABLE WITH A RANDOM SLOPE

TITLE: this is an example of a two-level

regression analysis for a continuous

dependent variable with a random slope and an observed covariate

DATA: FILE = ex9.2a.dat;

VARIABLE: NAMES = y x w xm clus;

WITHIN = x;

BETWEEN = w xm;

CLUSTER = clus;

DEFINE: CENTER x (GROUPMEAN);

ANALYSIS: TYPE = TWOLEVEL RANDOM;

MODEL:

%WITHIN%

s | y ON x;

%BETWEEN%

y s ON w xm;

y WITH s;

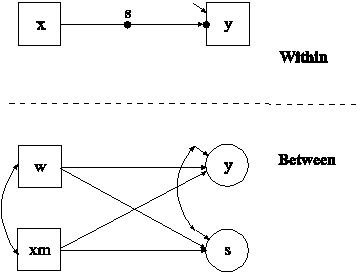
The difference between this example and the first part of Example 9.1 is that the model has both a random intercept and a random slope. In the within part of the model, the filled circle at the end of the arrow from x to y represents a random intercept that is referred to as y in the between part of the model. The filled circle on the arrow from x to y represents a random slope that is referred to as s in the between part of the model. In the between part of the model, the random intercept and random slope are shown in circles because they are continuous latent variables that vary across clusters. The observed cluster-level covariate xm takes the value of the mean of x for each cluster. The within and between parts of the model correspond to level 1 and level 2 of a conventional multilevel regression model with a random intercept and a random slope.

In the DEFINE command, the individual-level covariate x is centered using the cluster means for x. This is recommended when a random slope is estimated (Raudenbush & Bryk, 2002, p. 143).

In the between part of the model, the ON statement describes the linear regressions of the random intercept y and the random slope s on the observed cluster-level covariates w and xm. The intercepts and residual variances of s and y are estimated and the residuals are not correlated as the default. The WITH statement specifies that the residuals of s and y are correlated. The default estimator for this type of analysis is maximum likelihood with robust standard errors. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. An explanation of the other commands can be found in Example 9.1.

Following is the second part of the example that shows how to plot a cross-level interaction where the cluster-level covariate w moderates the influence of the within-level covariate x on y.

MODEL: %WITHIN%

s | y ON x;

%BETWEEN%

y ON w xm;

[s] (gam0);

s ON w (gam1)

xm;

y WITH s;

MODEL CONSTRAINT:

PLOT(ylow yhigh);

LOOP(level1,-3,3,0.01);

ylow = (gam0+gam1*(-1))*level1;

yhigh = (gam0+gam1*1)*level1;

PLOT: TYPE = PLOT2;

In MODEL CONSTRAINT, the LOOP option is used in conjunction with the PLOT option to create plots of variables. In this example, cross-level interaction effects defined in MODEL CONSTRAINT will be plotted. The PLOT option names the variables that will be plotted on the y-axis. The LOOP option names the variable that will be plotted on the x-axis, gives the numbers that are the lower and upper values of the variable, and the incremental value of the variable to be used in the computations. In this example, the variables ylow and yhigh will be on the y-axes and the variable level1 will be on the x-axes. The variable level1, representing the x covariate, varies over the range of x that is of interest such as three standard deviations away from its mean. The lower and upper values of level1 are -3 and 3 and 0.01 is the incremental value of level1 to use in the computations. When level1 appears in a MODEL CONSTRAINT statement involving a new parameter, that statement is evaluated for each value of level1 specified by the LOOP option. For example, the first value of level1 is -3; the second value of level1 is -3 plus 0.01 or -2.99; the third value of level1 is -2.99 plus 0.01 or -2.98; the last value of level1 is 3. Ylow and yhigh use the values -1 and 1 of the cluster-level covariate w to represent minus one standard deviation and plus one standard deviation from the mean for w. The cross-level interaction effects are evaluated at the value zero for the cluster-level covariate xm.

Using TYPE=PLOT2 in the PLOT command, the plots of ylow and yhigh and level1 can be viewed by choosing Loop plots from the Plot menu of the Mplus Editor. The plots present the computed values along with a 95% confidence interval. For Bayesian estimation, the default is credibility intervals of the posterior distribution with equal tail percentages. The CINTERVAL option of the OUTPUT command can be used to obtain credibility intervals of the posterior distribution that give the highest posterior density.

Following is the third part of the example that shows an alternative treatment of the observed covariate x.

TITLE: this is an example of a two-level

regression analysis for a continuous

dependent variable with a random slope and a latent covariate

DATA: FILE = ex9.2c.dat;

VARIABLE: NAMES = y x w clus;

BETWEEN = w;

CLUSTER = clus;

ANALYSIS: TYPE = TWOLEVEL RANDOM;

MODEL:

%WITHIN%

s | y ON x;

%BETWEEN%

y s ON w x;

y WITH s;

The difference between this part of the example and the first part of the example is that the covariate x is latent instead of observed on the between level. This is achieved when the individual-level observed covariate is modeled in both the within and between parts of the model. This is requested by not mentioning the observed covariate x on the WITHIN statement in the VARIABLE command. When a random slope is estimated, the observed covariate x is used on the within level and the latent variable covariate x_bj is used on the between level. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. An explanation of the other commands can be found in Example 9.1.

EXAMPLE 9.3: TWO-LEVEL PATH ANALYSIS WITH A CONTINUOUS AND A CATEGORICAL DEPENDENT VARIABLE

TITLE: this is an example of a two-level path

analysis with a continuous and a categorical dependent variable

DATA: FILE IS ex9.3.dat;

VARIABLE: NAMES ARE u y x1 x2 w clus;

CATEGORICAL = u;

WITHIN = x1 x2;

BETWEEN = w;

CLUSTER IS clus;

ANALYSIS: TYPE = TWOLEVEL;

ALGORITHM = INTEGRATION;

MODEL:

%WITHIN%

y ON x1 x2;

u ON y x2;

%BETWEEN%

y u ON w;

OUTPUT: TECH1 TECH8;

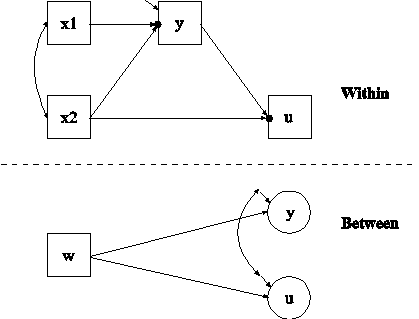
In this example, the two-level path analysis model shown in the picture above is estimated. The mediating variable y is a continuous variable and the dependent variable u is a binary or ordered categorical variable. The within part of the model describes the linear regression of y on x1 and x2 and the logistic regression of u on y and x2 where the intercepts in the two regressions are random effects that vary across the clusters and the slopes are fixed effects that do not vary across the clusters. In the within part of the model, the filled circles at the end of the arrows from x1 to y and x2 to u represent random intercepts that are referred to as y and u in the between part of the model. In the between part of the model, the random intercepts are shown in circles because they are continuous latent variables that vary across clusters. The between part of the model describes the linear regressions of the random intercepts y and u on a cluster-level covariate w.

The CATEGORICAL option is used to specify which dependent variables are treated as binary or ordered categorical (ordinal) variables in the model and its estimation. The program determines the number of categories of u. The dependent variable u could alternatively be an unordered categorical (nominal) variable. The NOMINAL option is used and a multinomial logistic regression is estimated.

In the within part of the model, the first ON statement describes the linear regression of y on the individual-level covariates x1 and x2 and the second ON statement describes the logistic regression of u on the mediating variable y and the individual-level covariate x2. The slopes in these regressions are fixed effects that do not vary across the clusters. The residual variance in the linear regression of y on x1 and x2 is estimated as the default. There is no residual variance to be estimated in the logistic regression of u on y and x2 because u is a binary or ordered categorical variable. In the between part of the model, the ON statement describes the linear regressions of the random intercepts y and u on the cluster-level covariate w. The intercept and residual variance of y and u are estimated as the default. The residual covariance between y and u is free to be estimated as the default.

By specifying ALGORITHM=INTEGRATION, a maximum likelihood estimator with robust standard errors using a numerical integration algorithm will be used. Note that numerical integration becomes increasingly more computationally demanding as the number of factors and the sample size increase. In this example, two dimensions of integration are used with a total of 225 integration points. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. The OUTPUT command is used to request additional output not included as the default. The TECH1 option is used to request the arrays containing parameter specifications and starting values for all free parameters in the model. The TECH8 option is used to request that the optimization history in estimating the model be printed in the output. TECH8 is printed to the screen during the computations as the default. TECH8 screen printing is useful for determining how long the analysis takes. An explanation of the other commands can be found in Example 9.1.

EXAMPLE 9.4: TWO-LEVEL PATH ANALYSIS WITH A CONTINUOUS, A CATEGORICAL, AND A CLUSTER-LEVEL OBSERVED DEPENDENT VARIABLE

TITLE: this is an example of a two-level path analysis with a continuous, a categorical, and a cluster-level observed dependent variable

DATA: FILE = ex9.4.dat;

VARIABLE: NAMES ARE u z y x w clus;

CATEGORICAL = u;

WITHIN = x;

BETWEEN = w z;

CLUSTER = clus;

ANALYSIS: TYPE = TWOLEVEL;

ESTIMATOR = WLSM;

MODEL:

%WITHIN%

u ON y x;

y ON x;

%BETWEEN%

u ON w y z;

y ON w;

z ON w;

y WITH z;

OUTPUT: TECH1;

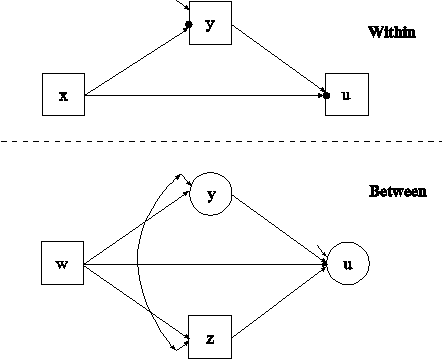
The difference between this example and Example 9.3 is that the between part of the model has an observed cluster-level mediating variable z and a latent mediating variable y that is a random intercept. The model is estimated using weighted least squares estimation instead of maximum likelihood.

By specifying ESTIMATOR=WLSM, a robust weighted least squares estimator using a diagonal weight matrix is used (Asparouhov & Muthén, 2007). The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator.

In the between part of the model, the first ON statement describes the linear regression of the random intercept u on the cluster-level covariate w, the random intercept y, and the observed cluster-level mediating variable z. The third ON statement describes the linear regression of the observed cluster-level mediating variable z on the cluster-level covariate w. An explanation of the other commands can be found in Examples 9.1 and 9.3.

EXAMPLE 9.5: TWO-LEVEL PATH ANALYSIS WITH CONTINUOUS DEPENDENT VARIABLES AND RANDOM SLOPES

TITLE: this is an example of two-level path

analysis with continuous dependent variables and random slopes

DATA: FILE IS ex9.5.dat;

VARIABLE: NAMES ARE y1 y2 x1 x2 w clus;

WITHIN = x1 x2;

BETWEEN = w;

CLUSTER IS clus;

ANALYSIS: TYPE = TWOLEVEL RANDOM;

MODEL:

%WITHIN%

s2 | y2 ON y1;

y2 ON x2;

s1 | y1 ON x2;

y1 ON x1;

%BETWEEN%

y1 y2 s1 s2 ON w;

OUTPUT: TECH1 TECH8;

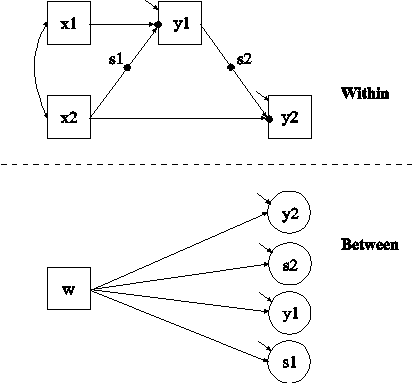
The difference between this example and Example 9.3 is that the model includes two random intercepts and two random slopes instead of two random intercepts and two fixed slopes and the dependent variable is continuous. In the within part of the model, the filled circle on the arrow from the covariate x2 to the mediating variable y1 represents a random slope and is referred to as s1 in the between part of the model. The filled circle on the arrow from the mediating variable y1 to the dependent variable y2 represents a random slope and is referred to as s2 in the between part of the model. In the between part of the model, the random slopes s1 and s2 are shown in circles because they are continuous latent variables that vary across clusters.

In the within part of the model, the | symbol is used in conjunction with TYPE=RANDOM to name and define the random slope variables in the model. The name on the left-hand side of the | symbol names the random slope variable. The statement on the right-hand side of the | symbol defines the random slope variable. Random slopes are defined using the ON option. In the first | statement, the random slope s2 is defined by the linear regression of the dependent variable y2 on the mediating variable y1. In the second | statement, the random slope s1 is defined by the linear regression of the mediating variable y1 on the individual-level covariate x2. The within-level residual variances of y1 and y2 are estimated as the default. The first ON statement describes the linear regression of the dependent variable y2 on the individual-level covariate x2. The second ON statement describes the linear regression of the mediating variable y1 on the individual-level covariate x1.

In the between part of the model, the ON statement describes the linear regressions of the random intercepts y1 and y2 and the random slopes s1 and s2 on the cluster-level covariate w. The intercepts and residual variances of y1, y2, s2, and s1 are estimated as the default. The residual covariances between y1, y2, s2, and s1 are fixed at zero as the default. This default can be overridden. The default estimator for this type of analysis is maximum likelihood with robust standard errors. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. An explanation of the other commands can be found in Examples 9.1 and 9.3.

EXAMPLE 9.6: TWO-LEVEL CFA WITH CONTINUOUS FACTOR INDICATORS AND COVARIATES

TITLE: this is an example of a two-level CFA with

continuous factor indicators and covariates

DATA: FILE IS ex9.6.dat;

VARIABLE: NAMES ARE y1-y4 x1 x2 w clus;

WITHIN = x1 x2;

BETWEEN = w;

CLUSTER = clus;

ANALYSIS: TYPE = TWOLEVEL;

MODEL:

%WITHIN%

fw BY y1-y4;

fw ON x1 x2;

%BETWEEN%

fb BY y1-y4;

y1-y4@0;

fb ON w;

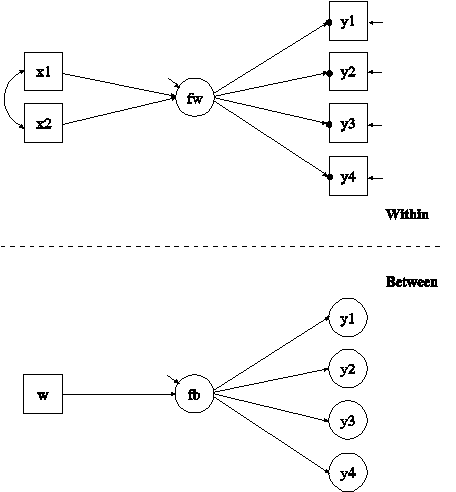
In this example, the two-level CFA model with continuous factor indicators, a between factor, and covariates shown in the picture above is estimated. In the within part of the model, the filled circles at the end of the arrows from the within factor fw to y1, y2, y3, and y4 represent random intercepts that are referred to as y1, y2, y3, and y4 in the between part of the model. In the between part of the model, the random intercepts are shown in circles because they are continuous latent variables that vary across clusters. They are indicators of the between factor fb. In this model, the residual variances for the factor indicators in the between part of the model are fixed at zero. If factor loadings are constrained to be equal across the within and the between levels, this implies a model where the regression of the within factor on x1 and x2 has a random intercept varying across the clusters.

In the between part of the model, the BY statement specifies that fb is measured by the random intercepts y1, y2, y3, and y4. The metric of the factor is set automatically by the program by fixing the first factor loading to one. This option can be overridden. The residual variances of the factor indicators are set to zero. The ON statement describes the regression of fb on the cluster-level covariate w. The residual variance of the factor is estimated as the default. The intercept of the factor is fixed at zero as the default. The default estimator for this type of analysis is maximum likelihood with robust standard errors. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. An explanation of the other commands can be found in Example 9.1.

EXAMPLE 9.7: TWO-LEVEL CFA WITH CATEGORICAL FACTOR INDICATORS AND COVARIATES

TITLE: this is an example of a two-level CFA with

categorical factor indicators and covariates

DATA: FILE IS ex9.7.dat;

VARIABLE: NAMES ARE u1-u4 x1 x2 w clus;

CATEGORICAL = u1-u4;

WITHIN = x1 x2;

BETWEEN = w;

CLUSTER = clus;

MISSING = ALL (999);

ANALYSIS: TYPE = TWOLEVEL;

MODEL:

%WITHIN%

fw BY u1-u4;

fw ON x1 x2;

%BETWEEN%

fb BY u1-u4;

fb ON w;

OUTPUT: TECH1 TECH8;

The difference between this example and Example 9.6 is that the factor indicators are binary or ordered categorical (ordinal) variables instead of continuous variables. The CATEGORICAL option is used to specify which dependent variables are treated as binary or ordered categorical (ordinal) variables in the model and its estimation. In the example above, all four factor indicators are binary or ordered categorical. The program determines the number of categories for each indicator. The default estimator for this type of analysis is maximum likelihood with robust standard errors using a numerical integration algorithm. Note that numerical integration becomes increasingly more computationally demanding as the number of factors and the sample size increase. In this example, two dimensions of integration are used with a total of 225 integration points. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator.

In the between part of the model, the residual variances of the random intercepts of the categorical factor indicators are fixed at zero as the default because the residual variances of random intercepts are often very small and require one dimension of numerical integration each. Weighted least squares estimation of between-level residual variances does not require numerical integration in estimating the model. An explanation of the other commands can be found in Examples 9.1 and 9.6.

EXAMPLE 9.8: TWO-LEVEL CFA WITH CONTINUOUS FACTOR INDICATORS, COVARIATES, AND RANDOM SLOPES

TITLE: this is an example of a two-level CFA with continuous factor indicators, covariates, and random slopes

DATA: FILE IS ex9.8.dat;

VARIABLE: NAMES ARE y1-y4 x1 x2 w clus;

CLUSTER = clus;

WITHIN = x1 x2;

BETWEEN = w;

ANALYSIS: TYPE = TWOLEVEL RANDOM;

MODEL:

%WITHIN%

fw BY y1-y4;

s1 | fw ON x1;

s2 | fw ON x2;

%BETWEEN%

fb BY y1-y4;

y1-y4@0;

fb s1 s2 ON w;

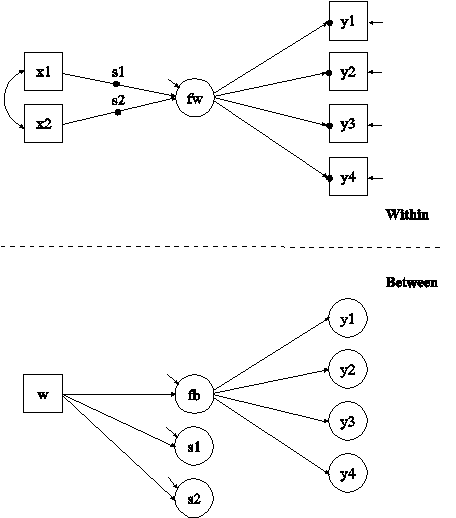
The difference between this example and Example 9.6 is that the model has random slopes in addition to random intercepts and the random slopes are regressed on a cluster-level covariate. In the within part of the model, the filled circles on the arrows from x1 and x2 to fw represent random slopes that are referred to as s1 and s2 in the between part of the model. In the between part of the model, the random slopes are shown in circles because they are latent variables that vary across clusters.

In the within part of the model, the | symbol is used in conjunction with TYPE=RANDOM to name and define the random slope variables in the model. The name on the left-hand side of the | symbol names the random slope variable. The statement on the right-hand side of the | symbol defines the random slope variable. Random slopes are defined using the ON option. In the first | statement, the random slope s1 is defined by the linear regression of the factor fw on the individual-level covariate x1. In the second | statement, the random slope s2 is defined by the linear regression of the factor fw on the individual-level covariate x2. The within-level residual variance of f1 is estimated as the default.

In the between part of the model, the ON statement describes the linear regressions of fb, s1, and s2 on the cluster-level covariate w. The residual variances of fb, s1, and s2 are estimated as the default. The residuals are not correlated as the default. The default estimator for this type of analysis is maximum likelihood with robust standard errors. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. An explanation of the other commands can be found in Examples 9.1 and 9.6.

EXAMPLE 9.9: TWO-LEVEL SEM WITH CATEGORICAL FACTOR INDICATORS ON THE WITHIN LEVEL AND CLUSTER-LEVEL CONTINUOUS OBSERVED AND RANDOM INTERCEPT FACTOR INDICATORS ON THE BETWEEN LEVEL

TITLE: this is an example of a two-level SEM with categorical factor indicators on the within level and cluster-level continuous observed and random intercept factor indicators on the between level

DATA: FILE IS ex9.9.dat;

VARIABLE: NAMES ARE u1-u6 y1-y4 x1 x2 w clus;

CATEGORICAL = u1-u6;

WITHIN = x1 x2;

BETWEEN = w y1-y4;

CLUSTER IS clus;

ANALYSIS: TYPE IS TWOLEVEL;

ESTIMATOR = WLSMV;

MODEL:

%WITHIN%

fw1 BY u1-u3;

fw2 BY u4-u6;

fw1 fw2 ON x1 x2;

%BETWEEN%

fb BY u1-u6;

f BY y1-y4;

fb ON w f;

f ON w;

SAVEDATA: SWMATRIX = ex9.9sw.dat;

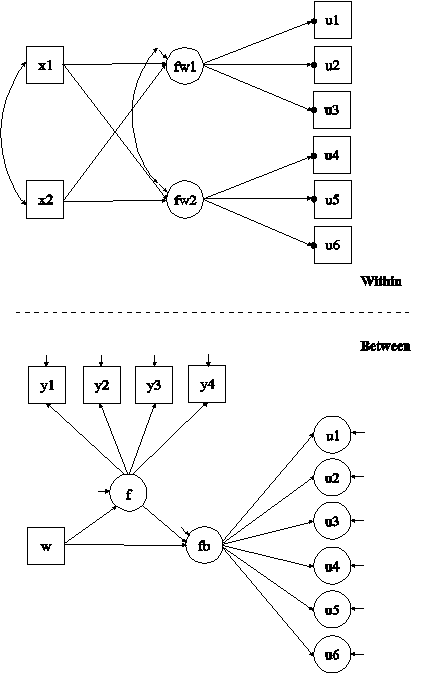
In this example, the model with two within factors and two between factors shown in the picture above is estimated. The within-level factor indicators are categorical. In the within part of the model, the filled circles at the end of the arrows from the within factor fw1 to u1, u2, and u3 and fw2 to u4, u5, and u6 represent random intercepts that are referred to as u1, u2, u3, u4, u5, and u6 in the between part of the model. In the between part of the model, the random intercepts are shown in circles because they are continuous latent variables that vary across clusters. The random intercepts are indicators of the between factor fb. This example illustrates the common finding of fewer between factors than within factors for the same set of factor indicators. The between factor f has observed cluster-level continuous variables as factor indicators.

By specifying ESTIMATOR=WLSMV, a robust weighted least squares estimator using a diagonal weight matrix will be used. The default estimator for this type of analysis is maximum likelihood with robust standard errors using a numerical integration algorithm. Note that numerical integration becomes increasingly more computationally demanding as the number of factors and the sample size increase. In this example, three dimensions of integration would be used with a total of 3,375 integration points. For models with many dimensions of integration and categorical outcomes, the weighted least squares estimator may improve computational speed. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator.

In the within part of the model, the first BY statement specifies that fw1 is measured by u1, u2, and u3. The second BY statement specifies that fw2 is measured by u4, u5, and u6. The metric of the factors are set automatically by the program by fixing the first factor loading for each factor to one. This option can be overridden. Residual variances of the latent response variables of the categorical factor indicators are not parameters in the model. They are fixed at one in line with the Theta parameterization. Residuals are not correlated as the default. The ON statement describes the linear regressions of fw1 and fw2 on the individual-level covariates x1 and x2. The residual variances of the factors are estimated as the default. The residuals of the factors are correlated as the default because residuals are correlated for latent variables that do not influence any other variable in the model except their own indicators. The intercepts of the factors are fixed at zero as the default.

In the between part of the model, the first BY statement specifies that fb is measured by the random intercepts u1, u2, u3, u4, u5, and u6. The metric of the factor is set automatically by the program by fixing the first factor loading to one. This option can be overridden. The residual variances of the factor indicators are estimated and the residuals are not correlated as the default. Unlike maximum likelihood estimation, weighted least squares estimation of between-level residual variances does not require numerical integration in estimating the model. The second BY statement specifies that f is measured by the cluster-level factor indicators y1, y2, y3, and y4. The residual variances of the factor indicators are estimated and the residuals are not correlated as the default. The first ON statement describes the linear regression of fb on the cluster-level covariate w and the factor f. The second ON statement describes the linear regression of f on the cluster-level covariate w. The residual variances of the factors are estimated as the default. The intercepts of the factors are fixed at zero as the default.

The SWMATRIX option of the SAVEDATA command is used with TYPE=TWOLEVEL and weighted least squares estimation to specify the name and location of the file that contains the within- and between-level sample statistics and their corresponding estimated asymptotic covariance matrix. It is recommended to save this information and use it in subsequent analyses along with the raw data to reduce computational time during model estimation. An explanation of the other commands can be found in Example 9.1.

EXAMPLE 9.10: TWO-LEVEL SEM WITH CONTINUOUS FACTOR INDICATORS AND A RANDOM SLOPE FOR A FACTOR

TITLE: this is an example of a two-level SEM with

continuous factor indicators and a random

slope for a factor

DATA: FILE IS ex9.10.dat;

VARIABLE: NAMES ARE y1-y5 w clus;

BETWEEN = w;

CLUSTER = clus;

ANALYSIS: TYPE = TWOLEVEL RANDOM;

ALGORITHM = INTEGRATION;

INTEGRATION = 10;

MODEL:

%WITHIN%

fw BY y1-y4;

s | y5 ON fw;

%BETWEEN%

fb BY y1-y4;

y1-y4@0;

y5 s ON fb w;

OUTPUT: TECH1 TECH8;

In this example, the two-level SEM with continuous factor indicators shown in the picture above is estimated. In the within part of the model, the filled circles at the end of the arrows from fw to the factor indicators y1, y2, y3, and y4 and the filled circle at the end of the arrow from fw to y5 represent random intercepts that are referred to as y1, y2, y3, y4, and y5 in the between part of the model. The filled circle on the arrow from fw to y5 represents a random slope that is referred to as s in the between part of the model. In the between part of the model, the random intercepts and random slope are shown in circles because they are continuous latent variables that vary across clusters.

By specifying TYPE=TWOLEVEL RANDOM in the ANALYSIS command, a multilevel model with random intercepts and random slopes will be estimated. By specifying ALGORITHM=INTEGRATION, a maximum likelihood estimator with robust standard errors using a numerical integration algorithm will be used. Note that numerical integration becomes increasingly more computationally demanding as the number of factors and the sample size increase. In this example, four dimensions of integration are used with a total of 10,000 integration points. The INTEGRATION option of the ANALYSIS command is used to change the number of integration points per dimension from the default of 15 to 10. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator.

In the within part of the model, the BY statement specifies that fw is measured by the factor indicators y1, y2, y3, and y4. The metric of the factor is set automatically by the program by fixing the first factor loading in each BY statement to one. This option can be overridden. The residual variances of the factor indicators are estimated and the residuals are uncorrelated as the default. The variance of the factor is estimated as the default.

In the between part of the model, the BY statement specifies that fb is measured by the random intercepts y1, y2, y3, and y4. The metric of the factor is set automatically by the program by fixing the first factor loading in the BY statement to one. This option can be overridden. The residual variances of the factor indicators are fixed at zero. The variance of the factor is estimated as the default. The ON statement describes the linear regressions of the random intercept y5 and the random slope s on the factor fb and the cluster-level covariate w. The intercepts and residual variances of y5 and s are estimated and their residuals are uncorrelated as the default.

EXAMPLE 9.11: TWO-LEVEL MULTIPLE GROUP CFA WITH CONTINUOUS FACTOR INDICATORS

TITLE: this is an example of a two-level

multiple group CFA with continuous

factor indicators

DATA: FILE IS ex9.11.dat;

VARIABLE: NAMES ARE y1-y6 g clus;

GROUPING = g (1 = g1 2 = g2);

CLUSTER = clus;

ANALYSIS: TYPE = TWOLEVEL;

MODEL:

%WITHIN%

fw1 BY y1-y3;

fw2 BY y4-y6;

%BETWEEN%

fb1 BY y1-y3;

fb2 BY y4-y6;

MODEL g2: %WITHIN%

fw1 BY y2-y3;

fw2 BY y5-y6;

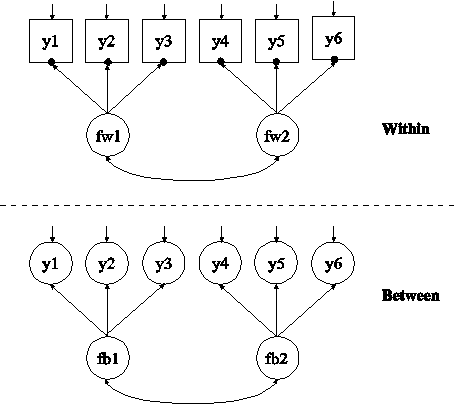
In this example, the two-level multiple group CFA with continuous factor indicators shown in the picture above is estimated. In the within part of the model, the filled circles at the end of the arrows from the within factors fw1 to y1, y2, and y3 and fw2 to y4, y5, and y6 represent random intercepts that are referred to as y1, y2, y3, y4, y5, and y6 in the between part of the model. In the between part of the model, the random intercepts are shown in circles because they are continuous latent variables that vary across clusters. The random intercepts are indicators of the between factors fb1 and fb2.

The GROUPING option of the VARIABLE command is used to identify the variable in the data set that contains information on group membership when the data for all groups are stored in a single data set. The information in parentheses after the grouping variable name assigns labels to the values of the grouping variable found in the data set. In the example above, observations with g equal to 1 are assigned the label g1, and individuals with g equal to 2 are assigned the label g2. These labels are used in conjunction with the MODEL command to specify model statements specific to each group. The grouping variable should be a cluster-level variable.

In multiple group analysis, two variations of the MODEL command are used. They are MODEL and MODEL followed by a label. MODEL describes the model to be estimated for all groups. The factor loadings and intercepts are held equal across groups as the default to specify measurement invariance. MODEL followed by a label describes differences between the overall model and the model for the group designated by the label.

In the within part of the model, the BY statements specify that fw1 is measured by y1, y2, and y3, and fw2 is measured by y4, y5, and y6. The metric of the factors is set automatically by the program by fixing the first factor loading in each BY statement to one. This option can be overridden. The variances of the factors are estimated as the default. The factors fw1 and fw2 are correlated as the default because they are independent (exogenous) variables. In the between part of the model, the BY statements specify that fb1 is measured by y1, y2, and y3, and fb2 is measured by y4, y5, and y6. The metric of the factor is set automatically by the program by fixing the first factor loading in each BY statement to one. This option can be overridden. The variances of the factors are estimated as the default. The factors fb1 and fb2 are correlated as the default because they are independent (exogenous) variables.

In the group-specific MODEL command for group 2, by specifying the within factor loadings for fw1 and fw2, the default equality constraints are relaxed and the factor loadings are no longer held equal across groups. The factor indicators that are fixed at one remain the same, in this case y1 and y4. The default estimator for this type of analysis is maximum likelihood with robust standard errors. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. An explanation of the other commands can be found in Example 9.1.

EXAMPLE 9.12: TWO-LEVEL GROWTH MODEL FOR A CONTINUOUS OUTCOME (THREE-LEVEL ANALYSIS)

TITLE: this is an example of a two-level growth model for a continuous outcome (three-level analysis)

DATA: FILE IS ex9.12.dat;

VARIABLE: NAMES ARE y1-y4 x w clus;

WITHIN = x;

BETWEEN = w;

CLUSTER = clus;

ANALYSIS: TYPE = TWOLEVEL;

MODEL:

%WITHIN%

iw sw | y1@0 y2@1 y3@2 y4@3;

y1-y4 (1);

iw sw ON x;

%BETWEEN%

ib sb | y1@0 y2@1 y3@2 y4@3;

y1-y4@0;

ib sb ON w;

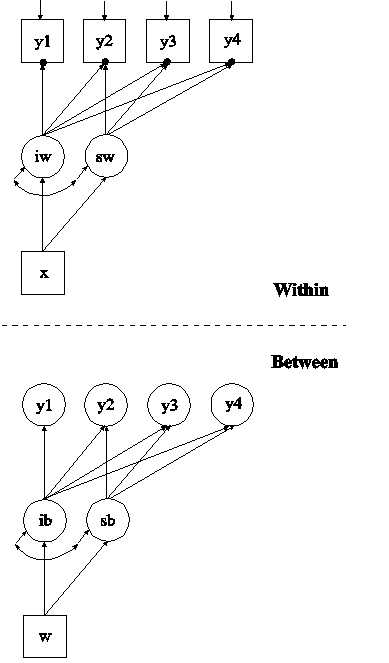
In this example, the two-level growth model for a continuous outcome (three-level analysis) shown in the picture above is estimated. In the within part of the model, the filled circles at the end of the arrows from the within growth factors iw and sw to y1, y2, y3, and y4 represent random intercepts that are referred to as y1, y2, y3, and y4 in the between part of the model. In the between part of the model, the random intercepts are shown in circles because they are continuous latent variables that vary across clusters.

In the within part of the model, the | statement names and defines the within intercept and slope factors for the growth model. The names iw and sw on the left-hand side of the | symbol are the names of the intercept and slope growth factors, respectively. The values on the right-hand side of the | symbol are the time scores for the slope growth factor. The time scores of the slope growth factor are fixed at 0, 1, 2, and 3 to define a linear growth model with equidistant time points. The zero time score for the slope growth factor at time point one defines the intercept growth factor as an initial status factor. The coefficients of the intercept growth factor are fixed at one as part of the growth model parameterization. The residual variances of the outcome variables are constrained to be equal over time in line with conventional multilevel growth modeling. This is done by placing (1) after them. The residual covariances of the outcome variables are fixed at zero as the default. Both of these restrictions can be overridden. The ON statement describes the linear regressions of the growth factors on the individual-level covariate x. The residual variances of the growth factors are free to be estimated as the default. The residuals of the growth factors are correlated as the default because residuals are correlated for latent variables that do not influence any other variable in the model except their own indicators.

In the between part of the model, the | statement names and defines the between intercept and slope factors for the growth model. The names ib and sb on the left-hand side of the | symbol are the names of the intercept and slope growth factors, respectively. The values on the right-hand side of the | symbol are the time scores for the slope growth factor. The time scores of the slope growth factor are fixed at 0, 1, 2, and 3 to define a linear growth model with equidistant time points. The zero time score for the slope growth factor at time point one defines the intercept factor as an initial status factor. The coefficients of the intercept growth factor are fixed at one as part of the growth model parameterization. The residual variances of the outcome variables are fixed at zero on the between level in line with conventional multilevel growth modeling. These residual variances can be estimated. The ON statement describes the linear regressions of the growth factors on the cluster-level covariate w. The residual variances and the residual covariance of the growth factors are free to be estimated as the default.

In the parameterization of the growth model shown here, the intercepts of the outcome variable at the four time points are fixed at zero as the default. The intercepts of the growth factors are estimated as the default in the between part of the model. The default estimator for this type of analysis is maximum likelihood with robust standard errors. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. An explanation of the other commands can be found in Example 9.1.

EXAMPLE 9.13: TWO-LEVEL GROWTH MODEL FOR A CATEGORICAL OUTCOME (THREE-LEVEL ANALYSIS)

TITLE: this is an example of a two-level

growth model for a categorical outcome (three-level analysis)

DATA: FILE IS ex9.13.dat;

VARIABLE: NAMES ARE u1-u4 x w clus;

CATEGORICAL = u1-u4;

WITHIN = x;

BETWEEN = w;

CLUSTER = clus;

ANALYSIS: TYPE = TWOLEVEL;

INTEGRATION = 7;

MODEL:

%WITHIN%

iw sw | u1@0 u2@1 u3@2 u4@3;

iw sw ON x;

%BETWEEN%

ib sb | u1@0 u2@1 u3@2 u4@3;

ib sb ON w;

OUTPUT: TECH1 TECH8;

The difference between this example and Example 9.12 is that the outcome variable is a binary or ordered categorical (ordinal) variable instead of a continuous variable.

The CATEGORICAL option is used to specify which dependent variables are treated as binary or ordered categorical (ordinal) variables in the model and its estimation. In the example above, u1, u2, u3, and u4 are binary or ordered categorical variables. They represent the outcome measured at four equidistant occasions.

The default estimator for this type of analysis is maximum likelihood with robust standard errors using a numerical integration algorithm. Note that numerical integration becomes increasingly more computationally demanding as the number of factors and the sample size increase. In this example, four dimensions of integration are used with a total of 2,401 integration points. The INTEGRATION option of the ANALYSIS command is used to change the number of integration points per dimension from the default of 15 to 7. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. For models with many dimensions of integration and categorical outcomes, the weighted least squares estimator may improve computational speed.

In the parameterization of the growth model shown here, the thresholds of the outcome variable at the four time points are held equal as the default and are estimated in the between part of the model. The intercept of the intercept growth factor is fixed at zero. The intercept of the slope growth factor is estimated as the default in the between part of the model. The residual variances of the growth factors are estimated as the default. The residuals of the growth factors are correlated as the default because residuals are correlated for latent variables that do not influence any other variable in the model except their own indicators. On the between level, the residual variances of the random intercepts u1, u2, u3, and u4 are fixed at zero as the default.

EXAMPLE 9.14: TWO-LEVEL GROWTH MODEL FOR A CONTINUOUS OUTCOME (THREE-LEVEL ANALYSIS) WITH VARIATION ON BOTH THE WITHIN AND BETWEEN LEVELS FOR A RANDOM SLOPE OF A TIME-VARYING COVARIATE

TITLE: this is an example of a two-level growth

model for a continuous outcome (three-

level analysis) with variation on both the within and between levels for a random slope of a time-varying covariate

DATA: FILE IS ex9.14.dat;

VARIABLE: NAMES ARE y1-y4 x a1-a4 w clus;

WITHIN = x a1-a4;

BETWEEN = w;

CLUSTER = clus;

ANALYSIS: TYPE = TWOLEVEL RANDOM;

ALGORITHM = INTEGRATION;

INTEGRATION = 10;

MODEL:

%WITHIN%

iw sw | y1@0 y2@1 y3@2 y4@3;

y1-y4 (1);

iw sw ON x;

s* | y1 ON a1;

s* | y2 ON a2;

s* | y3 ON a3;

s* | y4 ON a4;

%BETWEEN%

ib sb | y1@0 y2@1 y3@2 y4@3;

y1-y4@0;

ib sb s ON w;

OUTPUT: TECH1 TECH8;

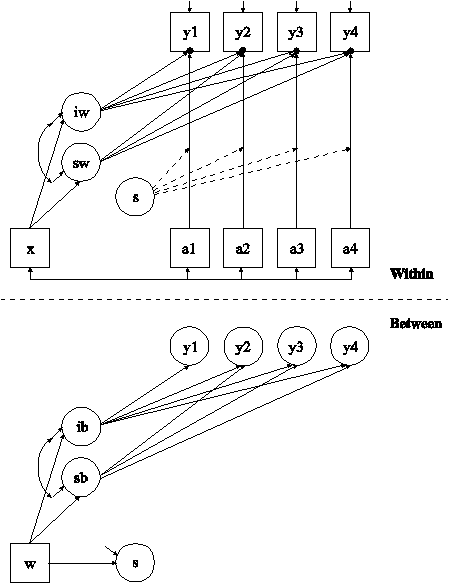
The difference between this example and Example 9.12 is that the model includes an individual-level time-varying covariate with a random slope that varies on both the within and between levels. In the within part of the model, the filled circles at the end of the arrows from a1 to y1, a2 to y2, a3 to y3, and a4 to y4 represent random intercepts that are referred to as y1, y2, y3, and y4 in the between part of the model. In the between part of the model, the random intercepts are shown in circles because they are continuous latent variables that vary across classes. The broken arrows from s to the arrows from a1 to y1, a2 to y2, a3 to y3, and a4 to y4 indicate that the slopes in these regressions are random. The s is shown in a circle in both the within and between parts of the model to represent a decomposition of the random slope into its within and between components.

The | symbol is used in conjunction with TYPE=RANDOM to name and define the random slope variables in the model. The name on the left-hand side of the | symbol names the random slope variable. The statement on the right-hand side of the | symbol defines the random slope variable. The random slope s is defined by the linear regressions of y1 on a1, y2 on a2, y3 on a3, and y4 on a4. Random slopes with the same name are treated as one variable during model estimation. The random intercepts for these regressions are referred to by using the name of the dependent variables in the regressions, that is, y1, y2, y3, and y4. The asterisk (*) following the s specifies that s will have variation on both the within and between levels. Without the asterisk (*), s would have variation on only the between level. An explanation of the other commands can be found in Examples 9.1 and 9.12.

EXAMPLE 9.15: TWO-LEVEL MULTIPLE INDICATOR GROWTH MODEL WITH CATEGORICAL OUTCOMES (THREE-LEVEL ANALYSIS)

TITLE: this is an example of a two-level multiple

indicator growth model with categorical

outcomes (three-level analysis)

DATA: FILE IS ex9.15.dat;

VARIABLE: NAMES ARE u11 u21 u31 u12 u22 u32 u13 u23

u33 clus;

CATEGORICAL = u11-u33;

CLUSTER = clus;

ANALYSIS: TYPE IS TWOLEVEL;

ESTIMATOR = WLSM;

MODEL:

%WITHIN%

f1w BY u11

u21-u31 (1-2);

f2w BY u12

u22-u32 (1-2);

f3w BY u13

u23-u33 (1-2);

iw sw | f1w@0 f2w@1 f3w@2;

%BETWEEN%

f1b BY u11

u21-u31 (1-2);

f2b BY u12

u22-u32 (1-2);

f3b BY u13

u23-u33 (1-2);

[u11$1 u12$1 u13$1] (3);

[u21$1 u22$1 u23$1] (4);

[u31$1 u32$1 u33$1] (5);

ib sb | f1b@0 f2b@1 f3b@2;

[f1b-f3b@0 ib@0 sb];

f1b-f3b (6);

SAVEDATA: SWMATRIX = ex9.15sw.dat;

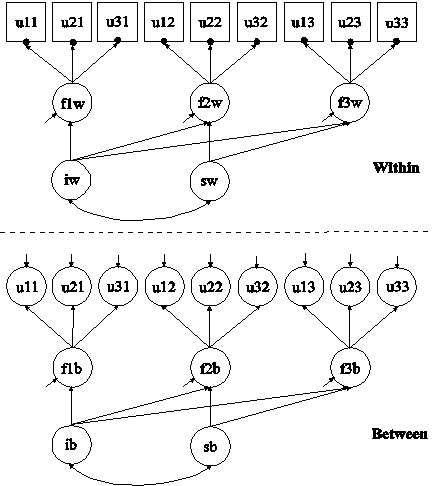
In this example, the two-level multiple indicator growth model with categorical outcomes (three-level analysis) shown in the picture above is estimated. The picture shows a factor measured by three indicators at three time points. In the within part of the model, the filled circles at the end of the arrows from the within factors f1w to u11, u21, and u31; f2w to u12, u22, and u32; and f3w to u13, u23, and u33 represent random intercepts that are referred to as u11, u21, u31, u12, u22, u32, u13, u23, and u33 in the between part of the model. In the between part of the model, the random intercepts are continuous latent variables that vary across clusters. The random intercepts are indicators of the between factors f1b, f2b, and f3b. In this model, the residual variances of the factor indicators in the between part of the model are estimated. The residuals are not correlated as the default. Taken together with the specification of equal factor loadings on the within and the between parts of the model, this implies a model where the regressions of the within factors on the growth factors have random intercepts that vary across the clusters.

By specifying ESTIMATOR=WLSM, a robust weighted least squares estimator using a diagonal weight matrix will be used. The default estimator for this type of analysis is maximum likelihood with robust standard errors using a numerical integration algorithm. Note that numerical integration becomes increasingly more computationally demanding as the number of factors and the sample size increase. For models with many dimensions of integration and categorical outcomes, the weighted least squares estimator may improve computational speed.

In the within part of the model, the three BY statements define a within-level factor at three time points. The metric of the three factors is set automatically by the program by fixing the first factor loading to one. This option can be overridden. The (1-2) following the factor loadings uses the list function to assign equality labels to these parameters. The label 1 is assigned to the factor loadings of u21, u22, and u23 which holds these factor loadings equal across time. The label 2 is assigned to the factor loadings of u31, u32, and u33 which holds these factor loadings equal across time. Residual variances of the latent response variables of the categorical factor indicators are not free parameters to be estimated in the model. They are fixed at one in line with the Theta parameterization. Residuals are not correlated as the default. The | statement names and defines the within intercept and slope growth factors for the growth model. The names iw and sw on the left-hand side of the | symbol are the names of the intercept and slope growth factors, respectively. The names and values on the right-hand side of the | symbol are the outcome and time scores for the slope growth factor. The time scores of the slope growth factor are fixed at 0, 1, and 2 to define a linear growth model with equidistant time points. The zero time score for the slope growth factor at time point one defines the intercept growth factor as an initial status factor. The coefficients of the intercept growth factor are fixed at one as part of the growth model parameterization. The variances of the growth factors are free to be estimated as the default. The covariance between the growth factors is free to be estimated as the default. The intercepts of the factors defined using BY statements are fixed at zero. The residual variances of the factors are free and not held equal across time. The residuals of the factors are uncorrelated in line with the default of residuals for first-order factors.

In the between part of the model, the first three BY statements define a between-level factor at three time points. The (1-2) following the factor loadings uses the list function to assign equality labels to these parameters. The label 1 is assigned to the factor loadings of u21, u22, and u23 which holds these factor loadings equal across time as well as across levels. The label 2 is assigned to the factor loadings of u31, u32, and u33 which holds these factor loadings equal across time as well as across levels. Time-invariant thresholds for the three indicators are specified using (3), (4), and (5) following the bracket statements. The residual variances of the factor indicators are free to be estimated. The | statement names and defines the between intercept and slope growth factors for the growth model. The names ib and sb on the left-hand side of the | symbol are the names of the intercept and slope growth factors, respectively. The values on the right-hand side of the | symbol are the time scores for the slope growth factor. The time scores of the slope growth factor are fixed at 0, 1, and 2 to define a linear growth model with equidistant time points. The zero time score for the slope growth factor at time point one defines the intercept growth factor as an initial status factor. The coefficients of the intercept growth factor are fixed at one as part of the growth model parameterization. In the parameterization of the growth model shown here, the intercept growth factor mean is fixed at zero as the default for identification purposes. The variances of the growth factors are free to be estimated as the default. The covariance between the growth factors is free to be estimated as the default. The intercepts of the factors defined using BY statements are fixed at zero. The residual variances of the factors are held equal across time. The residuals of the factors are uncorrelated in line with the default of residuals for first-order factors.

EXAMPLE 9.16: LINEAR GROWTH MODEL FOR A CONTINUOUS OUTCOME WITH TIME-INVARIANT AND TIME-VARYING COVARIATES CARRIED OUT AS A TWO-LEVEL GROWTH MODEL USING THE DATA WIDETOLONG COMMAND

TITLE: this is an example of a linear growth model for a continuous outcome with time-invariant and time-varying covariates carried out as a two-level growth model using the DATA WIDETOLONG command

DATA: FILE IS ex9.16.dat;

DATA WIDETOLONG:

WIDE = y11-y14 | a31-a34;

LONG = y | a3;

IDVARIABLE = person;

REPETITION = time;

VARIABLE: NAMES ARE y11-y14 x1 x2 a31-a34;

USEVARIABLE = x1 x2 y a3 person time;

CLUSTER = person;

WITHIN = time a3;

BETWEEN = x1 x2;

ANALYSIS: TYPE = TWOLEVEL RANDOM;

MODEL: %WITHIN%

s | y ON time;

y ON a3;

%BETWEEN%

y s ON x1 x2;

y WITH s;

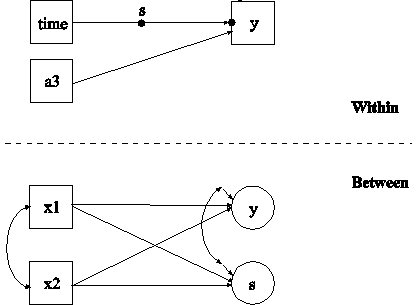
In this example, a linear growth model for a continuous outcome with time-invariant and time-varying covariates as shown in the picture above is estimated. As part of the analysis, the DATA WIDETOLONG command is used to rearrange the data from a multivariate wide format to a univariate long format. The model is similar to the one in Example 6.10 using multivariate wide format data. The differences are that the current model restricts the within-level residual variances to be equal across time and the within-level influence of the time-varying covariate on the outcome to be equal across time.

The WIDE option of the DATA WIDETOLONG command is used to identify sets of variables in the wide format data set that are to be converted into single variables in the long format data set. These variables must variables from the NAMES statement of the VARIABLE command. The two sets of variables y11, y12, y13, and y14 and a31, a32, a33, and a34 are identified. The LONG option is used to provide names for the new variables in the long format data set. The names y and a3 are the names of the new variables. The IDVARIABLE option is used to provide a name for the variable that provides information about the unit to which the record belongs. In univariate growth modeling, this is the person identifier which is used as a cluster variable. In this example, the name person is used. This option is not required. The default variable name is id. The REPETITION option is used to provide a name for the variable that contains information on the order in which the variables were measured. In this example, the name time is used. This option is not required. The default variable name is rep. The new variables must be mentioned on the USEVARIABLE statement of the VARIABLE command if they are used in the analysis. They must be placed after any original variables. The USEVARIABLES option lists the original variables x1 and x2 followed by the new variables y, a3, person, and time.

The CLUSTER option of the VARIABLE command is used to identify the variable that contains clustering information. In this example, the cluster variable person is the variable that was created using the IDVARIABLE option of the DATA WIDETOLONG command. The WITHIN option is used to identify the variables in the data set that are measured on the individual level and modeled only on the within level. They are specified to have no variance in the between part of the model. The BETWEEN option is used to identify the variables in the data set that are measured on the cluster level and modeled only on the between level. Variables not mentioned on the WITHIN or the BETWEEN statements are measured on the individual level and can be modeled on both the within and between levels.

In the between part of the model, the ON statement describes the linear regressions of the random intercept y and the random slope s on the covariates x1 and x2. The WITH statement is used to free the covariance between y and s. The default estimator for this type of analysis is maximum likelihood with robust standard errors. The estimator option of the ANALYSIS command can be used to select a different estimator. An explanation of the other commands can be found in Example 9.1.

EXAMPLE 9.17: TWO-LEVEL GROWTH MODEL FOR A COUNT OUTCOME USING A ZERO-INFLATED POISSON MODEL (THREE-LEVEL ANALYSIS)

TITLE: this is an example of a two-level growth model for a count outcome using a zero-inflated Poisson model (three-level analysis)

DATA: FILE = ex9.17.dat;

VARIABLE: NAMES = u1-u4 x w clus;

COUNT = u1-u4 (i);

CLUSTER = clus;

WITHIN = x;

BETWEEN = w;

ANALYSIS: TYPE = TWOLEVEL;

ALGORITHM = INTEGRATION;

INTEGRATION = 10;

MCONVERGENCE = 0.01;

MODEL: %WITHIN%

iw sw | u1@0 u2@1 u3@2 u4@3;

iiw siw | u1#1@0 u2#1@1 u3#1@2 u4#1@3;

sw@0;

siw@0;

iw WITH iiw;

iw ON x;

sw ON x;

%BETWEEN%

ib sb | u1@0 u2@1 u3@2 u4@3;

iib sib | u1#1@0 u2#1@1 u3#1@2 u4#1@3;

sb-sib@0;

ib ON w;

OUTPUT: TECH1 TECH8;

The difference between this example and Example 9.12 is that the outcome variable is a count variable instead of a continuous variable.

The COUNT option is used to specify which dependent variables are treated as count variables in the model and its estimation and whether a Poisson or zero-inflated Poisson model will be estimated. In the example above, u1, u2, u3, and u4 are count variables. The i in parentheses following u indicates that a zero-inflated Poisson model will be estimated.

By specifying ALGORITHM=INTEGRATION, a maximum likelihood estimator with robust standard errors using a numerical integration algorithm will be used. Note that numerical integration becomes increasingly more computationally demanding as the number of factors and the sample size increase. In this example, three dimensions of integration are used with a total of 1,000 integration points. The INTEGRATION option of the ANALYSIS command is used to change the number of integration points per dimension from the default of 15 to 10. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. The MCONVERGENCE option is used to change the observed-data log likelihood derivative convergence criterion for the EM algorithm from the default value of .001 to .01 because it is difficult to obtain high numerical precision in this example.

With a zero-inflated Poisson model, two growth models are estimated. In the within and between parts of the model, the first | statement describes the growth model for the count part of the outcome for individuals who are able to assume values of zero and above. The second | statement describes the growth model for the inflation part of the outcome, the probability of being unable to assume any value except zero. The binary latent inflation variable is referred to by adding to the name of the count variable the number sign (#) followed by the number 1. In the parameterization of the growth model for the count part of the outcome, the intercepts of the outcome variables at the four time points are fixed at zero as the default. In the parameterization of the growth model for the inflation part of the outcome, the intercepts of the outcome variable at the four time points are held equal as the default. In the within part of the model, the variances of the growth factors are estimated as the default, and the growth factor covariances are fixed at zero as the default. In the between part of the model, the mean of the growth factors for the count part of outcome are free. The mean of the intercept growth factor for the inflation part of the outcome is fixed at zero and the mean for the slope growth factor for the inflation part of the outcome is free. The variances of the growth factors are estimated as the default, and the growth factor covariances are fixed at zero as the default.

In the within part of the model, the variances of the slope growth factors sw and siw are fixed at zero. The ON statements describes the linear regressions of the intercept and slope growth factors iw and sw for the count part of the outcome on the covariate x. In the between part of the model, the variances of the intercept growth factor iib and the slope growth factors sb and sib are fixed at zero. The ON statement describes the linear regression of the intercept growth factor ib on the covariate w. An explanation of the other commands can be found in Examples 9.1 and 9.12.

EXAMPLE 9.18: TWO-LEVEL CONTINUOUS-TIME SURVIVAL ANALYSIS USING COX REGRESSION WITH A RANDOM INTERCEPT

TITLE: this is an example of a two-level continuous-time survival analysis using Cox regression with a random intercept

DATA: FILE = ex9.18.dat;

VARIABLE: NAMES = t x w tc clus;

CLUSTER = clus;

WITHIN = x;

BETWEEN = w;

SURVIVAL = t (ALL);

TIMECENSORED = tc (0 = NOT 1 = RIGHT);

ANALYSIS: TYPE = TWOLEVEL;

BASEHAZARD = OFF;

MODEL: %WITHIN%

t ON x;

%BETWEEN%

t ON w;

In this example, the two-level continuous-time survival analysis model shown in the picture above is estimated. This is the Cox regression model with a random intercept (Klein & Moeschberger, 1997; Hougaard, 2000). The profile likelihood method is used for estimation (Asparouhov et al., 2006).

The SURVIVAL option is used to identify the variables that contain information about time to event and to provide information about the time intervals in the baseline hazard function to be used in the analysis. The SURVIVAL option must be used in conjunction with the TIMECENSORED option. In this example, t is the variable that contains time to event information. By specifying the keyword ALL in parenthesis following the time-to-event variable, the time intervals are taken from the data. The TIMECENSORED option is used to identify the variables that contain information about right censoring. In this example, this variable is named tc. The information in parentheses specifies that the value zero represents no censoring and the value one represents right censoring. This is the default. The BASEHAZARD option of the ANALYSIS command is used with continuous-time survival analysis to specify if a non-parametric or a parametric baseline hazard function is used in the estimation of the model. The setting OFF specifies that a non-parametric baseline hazard function is used. This is the default.

The MODEL command is used to describe the model to be estimated. In multilevel models, a model is specified for both the within and between parts of the model. In the within part of the model, the loglinear regression of the time-to-event t on the covariate x is specified. In the between part of the model, the linear regression of the random intercept t on the cluster-level covariate w is specified. The residual variance of t is estimated. The default estimator for this type of analysis is maximum likelihood with robust standard errors. The estimator option of the ANALYSIS command can be used to select a different estimator. An explanation of the other commands can be found in Example 9.1.

EXAMPLE 9.19: TWO-LEVEL MIMIC MODEL WITH CONTINUOUS FACTOR INDICATORS, RANDOM FACTOR LOADINGS, TWO COVARIATES ON WITHIN, AND ONE COVARIATE ON BETWEEN WITH EQUAL LOADINGS ACROSS LEVELS

TITLE: this is an example of a two-level MIMIC

model with continuous factor indicators,

random factor loadings, two covariates on

within, and one covariate on between

with equal loadings across levels

DATA: FILE = ex9.19.dat;

VARIABLE: NAMES = y1-y4 x1 x2 w clus;

WITHIN = x1 x2;

BETWEEN = w;

CLUSTER = clus;

ANALYSIS: TYPE = TWOLEVEL RANDOM;

ESTIMATOR = BAYES;

PROCESSORS = 2;

BITERATIONS = (1000);

MODEL: %WITHIN%

s1-s4 | f BY y1-y4;

f@1;

f ON x1 x2;

%BETWEEN%

f ON w;

PLOT: TYPE = PLOT2;

OUTPUT: TECH1 TECH8;

In this example, a two-level MIMIC model with continuous factor indicators, random factor loadings, two covariates on within, and one covariate on between with equal loadings across levels is estimated. In the ANALYSIS command, TYPE=TWOLEVEL RANDOM is specified indicating that a two-level model will be estimated. By specifying ESTIMATOR=BAYES, a Bayesian analysis will be carried out. In Bayesian estimation, the default is to use two independent Markov chain Monte Carlo (MCMC) chains. If multiple processors are available, using PROCESSORS=2 will speed up computations. The BITERATIONS option is used to specify the maximum and minimum number of iterations for each Markov chain Monte Carlo (MCMC) chain when the potential scale reduction (PSR) convergence criterion (Gelman & Rubin, 1992) is used. Using a number in parentheses, the BITERATIONS option specifies that a minimum of 1000 and a maximum of the default of 50,000 iterations will be used.

In the within part of the model, the | symbol is used in conjunction with TYPE=RANDOM to name and define the random factor loading variables in the model. The name on the left-hand side of the | symbol names the random factor loading variable. The statement on the right-hand side of the | symbol defines the random factor loading variable. Random factor loadings are defined using the BY option. The random factor loading variables s1, s2, s3, and s4 are defined by the linear regression of the factor indicators y1, y2, y3, and y4 on the factor f. The factor variance is fixed at one to set the metric of the factor. The residual variances of y1 through y4 are estimated and the residuals are not correlated as the default. The ON statement describes the linear regression of f on the individual-level covariates x1 and x2. In the between part of the model, the ON statement describes the linear regression of the random intercept f on the cluster-level covariate w. The cluster-level residual variance of the factor is estimated. The intercepts and the cluster-level residual variances of y1 through y4 are estimated and the residuals are not correlated as the default.

By specifying TYPE=PLOT2 in the PLOT command, the following plots are available: posterior parameter distributions, posterior parameter trace plots, autocorrelation plots, posterior predictive checking scatterplots, and posterior predictive checking distribution plots. An explanation of the other commands can be found in Example 9.1.

Following is one alternative specification of the MODEL command where a different factor fb is specified in the between part of the model using the random intercepts as factor indicators. The residual variance of fb is estimated as the default.

MODEL: %WITHIN%

s1-s4 | f BY y1-y4;

f@1;

f ON x1 x2;

%BETWEEN%

fb BY y1-y4;

fb ON w;

Following is another alternative specification of the MODEL command where a factor is specified in the between part of the model using the random intercepts as factors indicators. The factor loadings of this factor are held equal to the means of the random factor loadings defined in the within part of the model.

MODEL: %WITHIN%

s1-s4 | f BY y1-y4;

f@1;

f ON x1 x2;

%BETWEEN%

fb BY y1-y4* (lam1-lam4);

fb ON w;

[s1-s4] (lam1-lam4);

EXAMPLE 9.20: THREE-LEVEL REGRESSION FOR A CONTINUOUS DEPENDENT VARIABLE

TITLE: this is an example of a three-level

regression for a continuous dependent variable

DATA: FILE = ex9.20.dat;

VARIABLE: NAMES = y x w z level2 level3;

CLUSTER = level3 level2;

WITHIN = x;

BETWEEN =(level2) w (level3) z;

ANALYSIS: TYPE = THREELEVEL RANDOM;

MODEL:

%WITHIN%

s1 | y ON x;

%BETWEEN level2%

s2 | y ON w;

s12 | s1 ON w;

y WITH s1;

%BETWEEN level3%

y ON z;

s1 ON z;

s2 ON z;

s12 ON z;

y WITH s1 s2 s12;

s1 WITH s2 s12;

s2 WITH s12;

OUTPUT: TECH1 TECH8;

In this example, the three-level regression with a continuous dependent variable shown in the picture above is estimated. The CLUSTER option is used to identify the variables in the data set that contain clustering information. Two cluster variables are used for a three-level model. The CLUSTER option specifies that level3 is the cluster variable for level 3 and level2 is the cluster variable for level 2. The cluster variable for the highest level must come first, that is, level 2 is nested in level 3.

The WITHIN option is used to identify the variables in the data set that are measured on the individual level and to specify the levels on which they are modeled. All variables on the WITHIN list must be measured on the individual level. An individual-level variable can be modeled on all or some levels. If a variable measured on the individual level is mentioned on the WITHIN list without a label, it is modeled on only level 1. It has no variance on levels 2 and 3. If a variable is not mentioned on the WITHIN list, it is modeled on all levels. The variable x can be modeled on only level 1. The variable y can be modeled on all levels.

The BETWEEN option is used to identify the variables in the data set that are measured on the cluster level(s) and to specify the level(s) on which they are modeled. All variables on the BETWEEN list must be measured on a cluster level. A cluster-level variable can be modeled on all or some cluster levels. For TYPE=THREELEVEL, if a variable measured on level 2 is mentioned on the BETWEEN list with a level 2 cluster label, it is modeled on only level 2. It has no variance on level 3. A variable measured on level 3 must be mentioned on the BETWEEN list with a level 3 cluster label. The variable w can be modeled on only level 2. The variable z can be modeled on only level 3.

In the ANALYSIS command, TYPE=THREELEVEL RANDOM is specified indicating that a three-level model will be estimated. In the within and level 2 parts of the model, the | symbol is used in conjunction with TYPE=RANDOM to name and define the random slope variables in the model. The name on the left-hand side of the | symbol names the random slope variable. The statement on the right-hand side of the | symbol defines the random slope variable. Random slopes are defined using the ON option. In the within part of the model, the random slope s1 is defined by the linear regression of y on the individual-level covariate x. The within-level residual variance of y is estimated as the default. In the level 2 part of the model, two random slopes are defined. The random slope s2 is defined by the linear regression of the level 2 random intercept y on the level 2 covariate w. The random slope s12 is defined by the linear regression of the level 2 random slope s1 on the level 2 covariate w. The level 2 residual variances of y and s1 are estimated and the residuals are not correlated as the default. The WITH statement specifies that the level 2 residuals of y and s1 are correlated.

In the level 3 part of the model, the first ON statement describes the linear regression of the level 3 random intercept y on the level 3 covariate z. The next three ON statements describe the linear regressions of the level 3 random slopes s1, s2, and s12 on the level 3 covariate z. The intercepts and level 3 residual variances of y, s1, s2, and s12 are estimated and the residuals are not correlated as the default. The WITH statements specify that the level 3 residuals of y, s1, s2, and s12 are correlated. The default estimator for this type of analysis is maximum likelihood with robust standard errors. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. An explanation of the other commands can be found in Examples 9.1 and 9.3.

EXAMPLE 9.21: THREE-LEVEL PATH ANALYSIS WITH A CONTINUOUS AND A CATEGORICAL DEPENDENT VARIABLE

TITLE: this an example of a three-level path

analysis with a continuous and a categorical dependent variable

DATA: FILE = ex9.21.dat;

VARIABLE: NAMES = u y2 y y3 x w z level2 level3;

CATEGORICAL = u;

CLUSTER = level3 level2;

WITHIN = x;

BETWEEN = y2 (level2) w (level3) z y3;

ANALYSIS: TYPE = THREELEVEL;

ESTIMATOR = BAYES;

PROCESSORS = 2;

BITERATIONS = (1000);

MODEL: %WITHIN%

u ON y x;

y ON x;

%BETWEEN level2%

u ON w y y2;

y ON w;

y2 ON w;

y WITH y2;

%BETWEEN level3%

u ON y y2;

y ON z;

y2 ON z;

y3 ON y y2;

y WITH y2;

u WITH y3;

OUTPUT: TECH1 TECH8;

In this example, the three-level path analysis with a continuous and a categorical dependent variable shown in the picture above is estimated. The CATEGORICAL option is used to specify which dependent variables are treated as binary or ordered categorical (ordinal) variables in the model and its estimation. In the example above, the variable u is binary or ordered categorical.

The BETWEEN option is used to identify the variables in the data set that are measured on the cluster level(s) and to specify the level(s) on which they are modeled. All variables on the BETWEEN list must be measured on a cluster level. A cluster-level variable can be modeled on all or some cluster levels. For TYPE=THREELEVEL, if a variable measured on level 2 is mentioned on the BETWEEN list without a label, it is modeled on levels 2 and 3. If a variable measured on level 2 is mentioned on the BETWEEN list with a level 2 cluster label, it is modeled on only level 2. It has no variance on level 3. A variable measured on level 3 must be mentioned on the BETWEEN list with a level 3 cluster label. The variable y2 can be modeled on levels 2 and 3. The variable w can be modeled on only level 2. The variables z and y3 can be modeled on only level 3.

In the ANALYSIS command, TYPE=THREELEVEL is specified indicating that a three-level model will be estimated. By specifying ESTIMATOR=BAYES, a Bayesian analysis will be carried out. In Bayesian estimation, the default is to use two independent Markov chain Monte Carlo (MCMC) chains. If multiple processors are available, using PROCESSORS=2 will speed up computations. The BITERATIONS option is used to specify the maximum and minimum number of iterations for each Markov chain Monte Carlo (MCMC) chain when the potential scale reduction (PSR) convergence criterion (Gelman & Rubin, 1992) is used. Using a number in parentheses, the BITERATIONS option specifies that a minimum of 1,000 and a maximum of the default of 50,000 iterations will be used.

In the within part of the model, the first ON statement describes the probit regression of u on the mediator y and the individual-level covariate x. The second ON statement describes the linear regression of the mediator y on the covariate x. The within-level residual variance of y is estimated as the default. In the level 2 part of the model, the first ON statement describes the linear regression of the level 2 random intercept u on the level 2 covariate w, the level 2 random intercept y, and the level 2 mediator y2. The second ON statement describes the linear regression of the level 2 random intercept y on the level 2 covariate w. The third ON statement describes the linear regression of the level 2 mediator y2 on the level 2 covariate w. The level 2 residual variances of u, y, and y2 are estimated and the residuals are not correlated as the default. The WITH statement specifies that the level 2 residuals of y and y2 are correlated. In the level 3 part of the model, the first ON statement describes the linear regression of the level 3 random intercept u on the level 3 random intercepts y and y2. The second ON statement describes the linear regression of the level 3 random intercept y on the level 3 covariate z. The third ON statement describes the linear regression of the level 3 random intercept y2 on the level 3 covariate z. The fourth ON statement describes the linear regression of the level 3 variable y3 on the level 3 random intercepts y and y2. The threshold of u; the intercepts of y, y2, and y3; and the level 3 residual variances of u, y, y2, and y3 are estimated and the residuals are not correlated as the default. The first WITH statement specifies that the residuals of y and y2 are correlated. The second WITH statement specifies that the residuals of u and y3 are correlated. An explanation of the other commands can be found in Examples 9.1, 9.3, and 9.20.

EXAMPLE 9.22: THREE-LEVEL MIMIC MODEL WITH CONTINUOUS FACTOR INDICATORS, TWO COVARIATES ON WITHIN, ONE COVARIATE ON BETWEEN LEVEL 2, AND ONE COVARIATE ON BETWEEN LEVEL 3 WITH RANDOM SLOPES ON BOTH WITHIN AND BETWEEN LEVEL 2

TITLE: this is an example of a three-level MIMIC

model with continuous factor indicators,

two covariates on within, one covariate on

between level 2, one covariate on between

level 3 with random slopes on both within

and between level 2

DATA: FILE = ex9.22.dat;

VARIABLE: NAMES = y1-y6 x1 x2 w z level2 level3;

CLUSTER = level3 level2;

WITHIN = x1 x2;

BETWEEN = (level2) w (level3) z;

ANALYSIS: TYPE = THREELEVEL RANDOM;

MODEL: %WITHIN%

fw1 BY y1-y3;

fw2 BY y4-y6;

fw1 ON x1;

s | fw2 ON x2;

%BETWEEN level2%

fb2 BY y1-y6;

sf2 | fb2 ON w;

ss | s ON w;

fb2 WITH s;

%BETWEEN level3%

fb3 BY y1-y6;

fb3 ON z;

s ON z;

sf2 ON z;

ss ON z;

fb3 WITH s sf2 ss;

s WITH sf2 ss;

sf2 WITH ss;

OUTPUT: TECH1 TECH8;

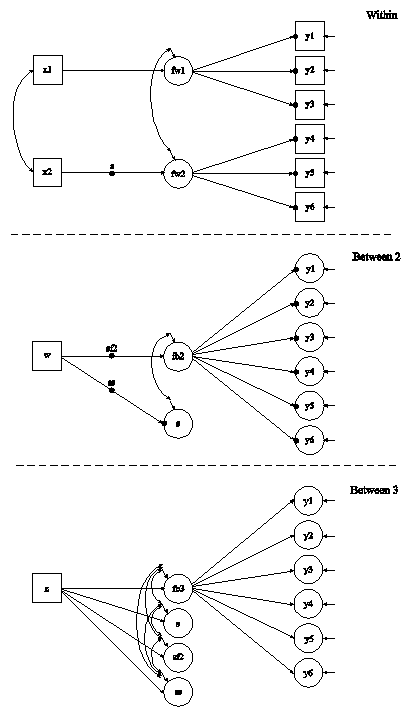
In this example, the three-level MIMIC model with continuous factor indicators, two covariates on within, one covariate on between level 2, one covariate on between level 3 with random slopes on both within and between level 2 shown in the picture above is estimated.

The WITHIN option is used to identify the variables in the data set that are measured on the individual level and to specify the levels on which they are modeled. All variables on the WITHIN list must be measured on the individual level. An individual-level variable can be modeled on all or some levels. If a variable measured on the individual level is mentioned on the WITHIN list without a label, it is modeled on only level 1. It has no variance on levels 2 and 3. If a variable is not mentioned on the WITHIN list, it is modeled on all levels. The variables x1 and x2 can be modeled on only level 1. The variables y1 through y6 can be modeled on all levels.

In the ANALYSIS command, TYPE=THREELEVEL RANDOM is specified indicating that a three-level model will be estimated. In the within part of the model, the first BY statement specifies that the factor fw1 is measured by y1 through y3. The second BY statement specifies that fw2 is measured by y4 through y6. The metric of the factors is set automatically by the program by fixing the first factor loading in each BY statement to one. This default can be overridden. The residual variances of the factor indicators are estimated and the residuals are not correlated as the default. The residual variances of the factors are estimated and the residuals are correlated as the default. The ON statement describes the linear regression of fw1 on the individual-level covariate x1.

In the within and level 2 parts of the model, the | symbol is used in conjunction with TYPE=RANDOM to name and define the random slope variables in the model. The name on the left-hand side of the | symbol names the random slope variable. The statement on the right-hand side of the | symbol defines the random slope variable. Random slopes are defined using the ON option. In the within part of the model, the random slope s is defined by the linear regression of fw2 on the individual-level covariate x2.

In the level 2 part of the model, the BY statement specifies that the factor fb2 is measured by the level 2 random intercepts y1 through y6. The metric of the factors is set automatically by the program by fixing the first factor loading in each BY statement to one. This default can be overridden. The level 2 residual variances of the factor indicators are estimated and the residuals are not correlated as the default. The variance of the factor is estimated as the default. The random slope sf2 is defined by the linear regression of fb2 on the level 2 covariate w. The random slope ss is defined by the linear regression of the random slope s on the level 2 covariate w. The level 2 residual variances of fb2 and s are estimated and the residuals are not correlated as the default.

In the level 3 part of the model, the BY statement specifies that the factor fb3 is measured by the level 3 random intercepts y1 through y6. The metric of the factors is set automatically by the program by fixing the first factor loading in each BY statement to one. This default can be overridden. The intercept and level 3 residual variances of the factor indicators are estimated and the residuals are not correlated as the default. The residual variance of the factor is estimated as the default. The first ON statement describes the linear regression of fb3 on the level 3 covariate z. The second ON statement describes the linear regression of the random slope s on the level 3 covariate z. The third ON statement describes the linear regression of the random slope sf2 on the level 3 covariate z. The fourth ON statement specifies the linear regression of the random slope ss on the level 3 covariate z. The intercepts of y1 through y6, s, sf2, and ss; and the level 3 residual variances of fb3, s, sf2, and ss are estimated and the residuals are not correlated as the default. The WITH statements specify that the level 3 residuals of fb3, s, sf2, and ss are correlated. The default estimator for this type of analysis is maximum likelihood with robust standard errors. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. An explanation of the other commands can be found in Examples 9.1, 9.3, and 9.20.

EXAMPLE 9.23: THREE-LEVEL GROWTH MODEL WITH A CONTINUOUS OUTCOME AND ONE COVARIATE ON EACH OF THE THREE LEVELS

TITLE: this is an example of a three-level growth

model with a continuous outcome and one

covariate on each of the three levels

DATA: FILE = ex9.23.dat;

VARIABLE: NAMES = y1-y4 x w z level2 level3;

CLUSTER = level3 level2;

WITHIN = x;

BETWEEN = (level2) w (level3) z;

ANALYSIS: TYPE = THREELEVEL;

MODEL: %WITHIN%

iw sw | y1@0 y2@1 y3@2 y4@3;

iw sw ON x;

%BETWEEN level2%

ib2 sb2 | y1@0 y2@1 y3@2 y4@3;

ib2 sb2 ON w;

%BETWEEN level3%

ib3 sb3 | y1@0 y2@1 y3@2 y4@3;

ib3 sb3 ON z;

y1-y4@0;

OUTPUT: TECH1 TECH8;

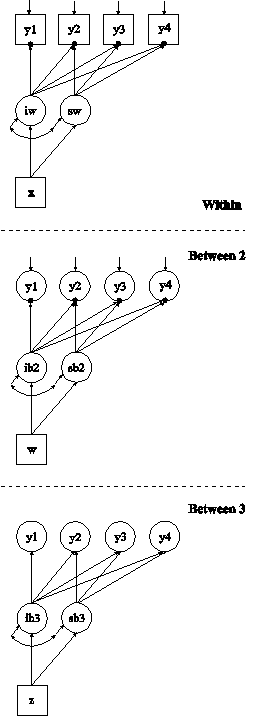
In this example, the three-level growth model with a continuous outcome and one covariate on each of the three levels shown in the picture above is estimated.

In the ANALYSIS command, TYPE=THREELEVEL is specified indicating that a three-level model will be estimated. In the within part of the model, the | symbol is used to name and define the within intercept and slope factors in a growth model. The names iw and sw on the left-hand side of the | symbol are the names of the intercept and slope growth factors, respectively. The statement on the right-hand side of the | symbol specifies the outcome and the time scores for the growth model. The time scores for the slope growth factor are fixed at 0, 1, 2, and 3 to define a linear growth model with equidistant time points. The zero time score for the slope growth factor at time point one defines the intercept growth factor as an initial status factor. The coefficients of the intercept growth factor are fixed at one as part of the growth model parameterization. The residual variances of y1 through y4 are estimated and allowed to be different across time and the residuals are not correlated as the default. In the parameterization of the growth model shown here, the intercepts of the outcome variables at the four time points are fixed at zero as the default. The ON statement describes the linear regression of the intercept and slope growth factors on the individual-level covariate x. The residual variances of the growth factors are estimated and the residuals are correlated as the default. The level 2 residual variances of y1 through y4 are estimated and allowed to be different across time and the residuals are not correlated as the default.

The growth model specified in the within part of the model is also specified on levels 2 and 3. In the level 2 part of the model, the ON statement describes the linear regression of the level 2 intercept and slope growth factors on the level 2 covariate w. The level 2 residual variances of the growth factors are estimated and the residuals are correlated as the default. In the level 3 part of the model, the ON statement describes the linear regression of the level 3 intercept and slope growth factors on the level 3 covariate z. The intercepts and level 3 residual variances of the growth factors are estimated and the residuals are correlated as the default. The level 3 residual variances of y1 through y4 are fixed at zero. The default estimator for this type of analysis is maximum likelihood with robust standard errors. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. An explanation of the other commands can be found in Examples 9.1, 9.3, and 9.20.

EXAMPLE 9.24: REGRESSION FOR A CONTINUOUS DEPENDENT VARIABLE USING CROSS-CLASSIFIED DATA

TITLE: this is an example of a regression for a continuous dependent variable using cross-classified data

DATA: FILE = ex9.24.dat;

VARIABLE: NAMES = y x1 x2 w z level2a level2b;

CLUSTER = level2b level2a;

WITHIN = x1 x2;

BETWEEN = (level2a) w (level2b) z;

ANALYSIS: TYPE = CROSSCLASSIFIED RANDOM;

ESTIMATOR = BAYES;

PROCESSORS = 2;

BITERATIONS = (2000);

MODEL: %WITHIN%

y ON x1;

s | y ON x2;

%BETWEEN level2a%

y ON w;

s ON w;

y WITH s;

%BETWEEN level2b%

y ON z;

s ON z;

y WITH s;

OUTPUT: TECH1 TECH8;

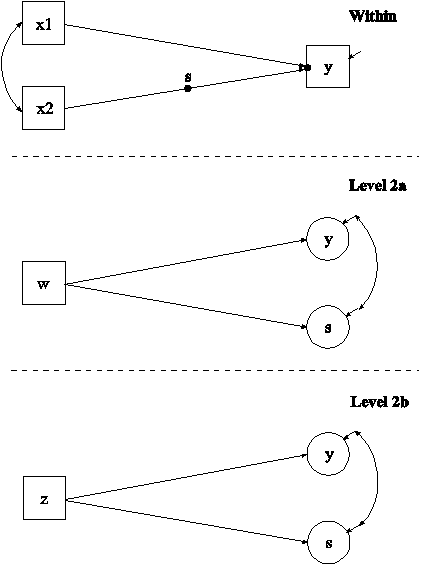
In this example, the regression for a continuous dependent variable using cross-classified data shown in the picture above is estimated. The CLUSTER option is used to identify the variables in the data set that contain clustering information. Two cluster variables are used for a cross-classified model. The CLUSTER option specifies that level2b is the cluster variable for level 2b and level2a is the cluster variable for level 2a.

The WITHIN option is used to identify the variables in the data set that are measured on the individual level and to specify the levels on which they are modeled. All variables on the WITHIN list must be measured on the individual level. An individual-level variable can be modeled on all or some levels. If a variable measured on the individual level is mentioned on the WITHIN list without a label, it is modeled on only level 1. It has no variance on levels 2a and 2b. If a variable is not mentioned on the WITHIN list, it is modeled on all levels. The variables x1 and x2 can be modeled on only level 1. The variable y can be modeled on all levels.

The BETWEEN option is used to identify the variables in the data set that are measured on the cluster level(s) and to specify the level(s) on which they are modeled. All variables on the BETWEEN list must be measured on a cluster level. For TYPE=CROSSCLASSIFIED, a variable measured on level 2a must be mentioned on the BETWEEN list with a level 2a cluster label. It can be modeled on only level 2a. A variable measured on level 2b must be mentioned on the BETWEEN list with a level 2b cluster label. It can be modeled on only level 2b. The variable w can be modeled on only level 2a. The variable z can be modeled on only level 2b.

In the ANALYSIS command, TYPE=CROSSCLASSIFIED RANDOM is specified indicating that a cross-classified model will be estimated. By specifying ESTIMATOR=BAYES, a Bayesian analysis will be carried out. In Bayesian estimation, the default is to use two independent Markov chain Monte Carlo (MCMC) chains. If multiple processors are available, using PROCESSORS=2 will speed up computations. The BITERATIONS option is used to specify the maximum and minimum number of iterations for each Markov chain Monte Carlo (MCMC) chain when the potential scale reduction (PSR) convergence criterion (Gelman & Rubin, 1992) is used. Using a number in parentheses, the BITERATIONS option specifies that a minimum of 2000 and a maximum of the default of 50,000 iterations will be used.

In the within part of the model, the ON statement describes the linear regression of y on the individual-level covariate x1. The residual variance of y is estimated as the default. The | symbol is used in conjunction with TYPE=RANDOM to name and define the random slope variables in the model. The name on the left-hand side of the | symbol names the random slope variable. The statement on the right-hand side of the | symbol defines the random slope variable. Random slopes are defined using the ON option. The random slope s is defined by the linear regression of y on the individual-level covariate x2. In the level 2a part of the model, the first ON statement describes the linear regression of the level 2a random intercept y on the level 2a covariate w. The second ON statement describes the linear regression of the level 2a random slope s on the level 2a covariate w. The residuals of y and s are estimated and the residuals are not correlated as the default. The WITH statement specifies that the residuals of y and s are correlated. In the level 2b part of the model, the first ON statement describes the linear regression of the level 2b random intercept y on the level 2b covariate z. The second ON statement describes the linear regression of the level 2b random slope s on the level 2b covariate z. The residual variances of y and s are estimated and the residuals are not correlated as the default. The WITH statement specifies that the residuals of y and s are correlated. The intercepts of y and s are estimated as the default on level 2b. An explanation of the other commands can be found in Examples 9.1 and 9.3.

EXAMPLE 9.25: PATH ANALYSIS WITH CONTINUOUS DEPENDENT VARIABLES USING CROSS-CLASSIFIED DATA

TITLE: this is an example of path analysis with continuous dependent variables using cross-classified data

DATA: FILE = ex9.25.dat;

VARIABLE: NAMES = y1 y2 x w z level2a level2b;

CLUSTER = level2b level2a;

WITHIN = x;

BETWEEN = (level2a) w (level2b) z;

ANALYSIS: TYPE = CROSSCLASSIFIED;

ESTIMATOR = BAYES;

PROCESSORS = 2;

MODEL: %WITHIN%

y2 ON y1 x;

y1 ON x;

%BETWEEN level2a%

y1 y2 ON w;

y1 WITH y2;

%BETWEEN level2b%

y1 y2 ON z;

y1 WITH y2;

OUTPUT: TECH1 TECH8;

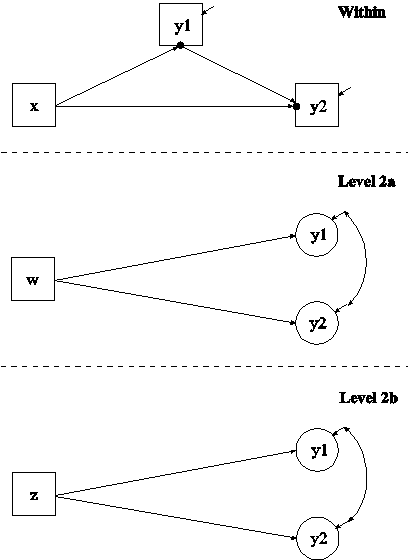
In this example, the path analysis with continuous dependent variables using cross-classified data shown in the picture above is estimated. The WITHIN option is used to identify the variables in the data set that are measured on the individual level and to specify the levels on which they are modeled. All variables on the WITHIN list must be measured on the individual level. An individual-level variable can be modeled on all or some levels. If a variable measured on the individual level is mentioned on the WITHIN list without a label, it is modeled on only level 1. It has no variance on levels 2a and 2b. If a variable is not mentioned on the WITHIN list, it is modeled on all levels. The variable x can be modeled on only level 1. The variables y1 and y2 can be modeled on all levels.

The BETWEEN option is used to identify the variables in the data set that are measured on the cluster level(s) and to specify the level(s) on which they are modeled. All variables on the BETWEEN list must be measured on a cluster level. For TYPE=CROSSCLASSIFIED, a variable measured on level 2a must be mentioned on the BETWEEN list with a level 2a cluster label. It can be modeled on only level 2a. A variable measured on level 2b must be mentioned on the BETWEEN list with a level 2b cluster label. It can be modeled on only level 2b. The variable w can be modeled on only level 2a. The variable z can be modeled on only level 2b.

In the ANALYSIS command, TYPE=CROSSCLASSIFIED is specified indicating that a cross-classified model will be estimated. By specifying ESTIMATOR=BAYES, a Bayesian analysis will be carried out. No other estimators are available. In Bayesian estimation, the default is to use two independent Markov chain Monte Carlo (MCMC) chains. If multiple processors are available, using PROCESSORS=2 will speed up computations.

In the within part of the model, the first ON statement describes the linear regression of y2 on the mediator y1 and the individual-level covariate x. The second ON statement describes the linear regression of y1 on the individual-level covariate x. The residuals of y1 and y2 are estimated and the residual are not correlated as the default. In the level 2a part of the model, the first ON statement describes the linear regressions of the level 2a intercepts y1 and y2 on the level 2a covariate w. The level 2a residuals are estimated and the residuals are not correlated as the default. The WITH statement specifies that the level 2a residuals of y1 and y2 are correlated. In the level 2b part of the model, the first ON statement describes the linear regression of the level 2b random intercepts y1 and y2 on the level 2b covariate z. The level 2b residuals are estimated and the residuals are not correlated as the default. The WITH statement specifies that the level 2b residuals of y1 and y2 are correlated. The intercepts of y1 and y2 are estimated as the default on level 2b. An explanation of the other commands can be found in Examples 9.1, 9.3, and 9.24.

EXAMPLE 9.26: IRT WITH RANDOM BINARY ITEMS USING CROSS-CLASSIFIED DATA

TITLE: this is an example of IRT with random binary items using cross-classified

data

DATA: FILE = ex9.26.dat;

VARIABLE: NAMES = u subject item;

CATEGORICAL = u;

CLUSTER = item subject;

ANALYSIS: TYPE = CROSSCLASSIFIED RANDOM;

ESTIMATOR = BAYES;

PROCESSORS = 2;

MODEL: %WITHIN%

%BETWEEN subject%

s | f BY u;

f@1;

u@0;

%BETWEEN item%

u; [u$1];

s; [s];

OUTPUT: TECH1 TECH8;

In this example, an IRT with random binary items using cross-classified data is estimated (Fox, 2010). Both the intercepts and factor loadings of the set of items are random. The CATEGORICAL option is used to specify which dependent variables are treated as binary or ordered categorical (ordinal) variables in the model and its estimation. In the example above, the variable u is binary or ordered categorical. The CLUSTER option is used to identify the variables in the data set that contain clustering information. Two cluster variables are used for a cross-classified model. The CLUSTER option specifies that item is the cluster variable for the item level and subject is the cluster variable for the subject level. The fastest moving level must come first.

The WITHIN option is used to identify the variables in the data set that are measured on the individual level and to specify the levels on which they are modeled. If a variable is not mentioned on the WITHIN list, it is modeled on all levels. The variable u can be modeled on the subject and item levels.

The within part of the model is not used in this example. In the subject part of the model, the | symbol is used in conjunction with TYPE=RANDOM to name and define the random factor loading variables in the model. The name on the left-hand side of the | symbol names the random factor loading variable. The statement on the right-hand side of the | symbol defines the random factor loading variable. Random factor loadings are defined using the BY option. The random factor loading variable s is defined by the probit regression of u on the factor f. The factor variance is fixed at one to set the metric of the factor. The across-subject variance of u is fixed at zero. In the item part of the model, the variance of the random intercept u, the threshold of u, and the mean and variance of the random factor loading s are estimated as the default. An explanation of the other commands can be found in Examples 9.1, 9.3, and 9.24.

EXAMPLE 9.27: MULTIPLE INDICATOR GROWTH MODEL WITH RANDOM INTERCEPTS AND FACTOR LOADINGS USING CROSS-CLASSIFIED DATA

TITLE: this is an example of a multiple indicator growth model with random intercepts and factor loadings using cross-classified data

DATA: FILE = ex9.27.dat;

VARIABLE: NAMES = y1-y3 time subject;

USEVARIABLES = y1-y3 timescor;

CLUSTER = subject time;

WITHIN = timescor (time) y1-y3;

DEFINE: timescor = (time-1)/100;

ANALYSIS: TYPE = CROSSCLASSIFIED RANDOM;

ESTIMATOR = BAYES;

PROCESSORS = 2;

BITERATIONS = (1000);

MODEL: %WITHIN%

s1-s3 | f BY y1-y3;

f@1;

s | f ON timescor;

y1-y3; [y1-y3@0];

%BETWEEN time%

s1-s3; [s1-s3];

y1-y3; [y1-y3@0];

s@0; [s@0];

%BETWEEN subject%

f; [f];

s1-s3@0; [s1-s3@0];

s; [s];

OUTPUT: TECH1 TECH8;

In this example, a multiple indicator growth model with random intercepts and factor loadings using cross-classified data is estimated. The WITHIN option is used to identify the variables in the data set that are measured on the individual level and to specify the levels on which they are modeled. All variables on the WITHIN list must be measured on the individual level. An individual-level variable can be modeled on all or some levels. If a variable measured on the individual level is mentioned on the WITHIN list without a label, it is modeled on only level 1. It has no variance on the time and subject levels. If it is mentioned on the WITHIN list with a time cluster label, it is modeled on levels 1 and on the time level. It has no variance on the subject level. The variable timescor can be modeled on only level 1. The variables y1, y2, and y3 can be modeled on levels 1 and the time level. The DEFINE command is used to transform existing variables and to create new variables. The new variable timescor is a time score variable centered at the first time point.

In the ANALYSIS command, TYPE=CROSSCLASSIFIED RANDOM is specified indicating that a cross-classified model will be estimated. By specifying ESTIMATOR=BAYES, a Bayesian analysis will be carried out. In Bayesian estimation, the default is to use two independent Markov chain Monte Carlo (MCMC) chains. If multiple processors are available, using PROCESSORS=2 will speed up computations. The BITERATIONS option is used to specify the maximum and minimum number of iterations for each Markov chain Monte Carlo (MCMC) chain when the potential scale reduction (PSR) convergence criterion (Gelman & Rubin, 1992) is used. Using a number in parentheses, the BITERATIONS option specifies that a minimum of 1000 and a maximum of the default of 50,000 iterations will be used.

In the time part of the model, the means and variances of the random factor loadings s1, s2, and s3 and the variances of the random intercepts y1, y2, and y3 are estimated. The intercepts of y1, y2, and y3 are fixed at zero as part of the growth model parameterization. The variances of the random factor loadings s1, s2, and s3 and the variances of the random intercepts y1, y2, and y3 represent measurement non-invariance across time. The mean and variance of the random slope growth factor s are fixed at zero.

In the subject part of the model, f is a random intercept growth factor. Its mean and variance are estimated. The means and variances of the random factor loadings s1, s2, and s3 are fixed at zero. The mean and variance of the random slope growth factor s are estimated. An explanation of the other commands can be found in Examples 9.1, 9.3, and 9.24.

EXAMPLE 9.28: TWO-LEVEL REGRESSION ANALYSIS FOR A CONTINUOUS DEPENDENT VARIABLE WITH A RANDOM INTERCEPT AND A RANDOM RESIDUAL VARIANCE

TITLE: this is an example of a two-level regression analysis for a continuous dependent variable with a random intercept and a random residual variance

DATA: FILE = ex9.28.dat;

VARIABLE: NAMES ARE z y x w xm clus;

WITHIN = x;

BETWEEN = w xm z;

CLUSTER = clus;

ANALYSIS: TYPE = TWOLEVEL RANDOM;

ESTIMATOR = BAYES;

PROCESSORS = 2;

BITERATIONS = (2000);

MODEL: %WITHIN%

y ON x;

logv | y;

%BETWEEN%

y ON w xm;

logv ON w xm;

y WITH logv;

z ON y logv;

OUTPUT: TECH1 TECH8;

PLOT: TYPE = PLOT3;

In this example, the two-level regression analysis for a continuous dependent variable with a random intercept and a random residual variance shown in the picture above is estimated. The dependent variable y in this regression is continuous. Both the intercept and residual variance are random. In the within part of the model, the filled circle at the end of the arrow from x to y represents a random intercept that is referred to as y in the between part of the model. The filled circle at the end of the residual arrow pointing to y represents a random residual variance that is referred to as logv in the between part of the model. In the between part of the model, the random intercept and random residual variance are shown in circles because they are continuous latent variables that vary across clusters. The log of the random residual variance is used in the model.

In the ANALYSIS command, TYPE=TWOLEVEL RANDOM is specified indicating that a two-level model will be estimated. By specifying ESTIMATOR=BAYES, a Bayesian analysis will be carried out. In Bayesian estimation, the default is to use two independent Markov chain Monte Carlo (MCMC) chains. If multiple processors are available, using PROCESSORS=2 will speed up computations. The BITERATIONS option is used to specify the maximum and minimum number of iterations for each Markov chain Monte Carlo (MCMC) chain when the potential scale reduction (PSR) convergence criterion (Gelman & Rubin, 1992) is used. Using a number in parentheses, the BITERATIONS option specifies that a minimum of 2,000 and a maximum of the default of 50,000 iterations will be used.

In the within part of the model, the ON statement describes the linear regression of y on the observed individual-level covariate x. The residual variance of y is estimated as the default. The | symbol is used in conjunction with TYPE=RANDOM to name and define the random residual variance. The name on the left-hand side of the | symbol names the log of the random residual variance. The name on the right-hand side of the | symbol specifies the name of the variable that has a random residual variance. Logv is the random residual variance for y.

In the between part of the model, the first ON statement describes the linear regression of the random intercept y on the observed cluster-level covariates w and xm. The second ON statement describes the linear regression of the log of the random residual variance logv on the cluster-level covariates w and xm. The intercept and residual variance of y and logv are estimated as the default. The WITH statement specifies that the residuals of y and logv are correlated. The third ON statement describes the linear regression of the cluster-level dependent variable z on the random intercept and the log of the random residual variance. The intercept and residual variance of z are estimated as the default.

The OUTPUT command is used to request additional output not included as the default. The TECH1 option is used to request the arrays containing parameter specifications and starting values for all free parameters in the model. The TECH8 option is used to request that the optimization history in estimating the model be printed in the output. TECH8 is printed to the screen during the computations as the default. TECH8 screen printing is useful for determining how long the analysis takes and to check convergence using the PSR convergence criterion. The PLOT command is used to request graphical displays of observed data and analysis results. These graphical displays can be viewed after the analysis is completed using a post-processing graphics module. The trace plot and autocorrelation plot can be used to monitor the MCMC iterations in terms of convergence and quality of the posterior distribution for each parameter. The posterior distribution plot shows the complete posterior distribution of the parameter estimate. An explanation of the other commands can be found in Example 9.1.

EXAMPLE 9.29: TWO-LEVEL CONFIRMATORY FACTOR ANALYSIS (CFA) WITH CONTINUOUS FACTOR INDICATORS, COVARIATES, AND A FACTOR WITH A RANDOM RESIDUAL VARIANCE

TITLE: this is an example of a two-level confirmatory factor analysis (CFA)

with continuous factor indicators,

covariates, and a factor with a random residual variance

DATA: FILE = ex9.29.dat;

VARIABLE: NAMES ARE y1-y4 x1 x2 w clus;

WITHIN = x1 x2;

BETWEEN = w;

CLUSTER = clus;

ANALYSIS: TYPE = TWOLEVEL RANDOM;

ESTIMATOR = BAYES;

PROCESSORS = 2;

BITERATIONS = (10000);

MODEL: %WITHIN%

fw BY y1-y4;

fw ON x1 x2;

logv | fw;

%BETWEEN%

fb BY y1-y4;

fb ON w;

logv ON w;

OUTPUT: TECH1 TECH8;

PLOT: TYPE = PLOT3;

In this example, the two-level CFA model with continuous factor indicators, covariates, and a factor with a random residual variance shown in the picture above is estimated. In the within part of the model, the filled circles at the end of the arrows from the within factor fw to y1, y2, y3, and y4 represent random intercepts that are referred to as y1, y2, y3, and y4 in the between part of the model. The filled circle at the end of the residual arrow pointing to fw represents a random residual variance that is referred to as logv in the between part of the model. In the between part of the model, the random intercepts are shown in circles because they are continuous latent variables that vary across clusters. They are indicators of the between factor fb. The log of the random residual variance is used in the model.

The BITERATIONS option is used to specify the maximum and minimum number of iterations for each Markov chain Monte Carlo (MCMC) chain when the potential scale reduction (PSR) convergence criterion (Gelman & Rubin, 1992) is used. Using a number in parentheses, the BITERATIONS option specifies that a minimum of 10,000 and a maximum of the default of 50,000 iterations will be used. The minimum is relatively large because this model may be more difficult to estimate.

In the within part of the model, the BY statement specifies that fw is measured by y1, y2, y3, and y4. The metric of the factor is set automatically by the program by fixing the first factor loading to one. This option can be overridden. The residual variances of the factor indicators are estimated and the residuals are not correlated as the default. The ON statement describes the linear regression of fw on the individual-level covariates x1 and x2. The | symbol is used in conjunction with TYPE=RANDOM to name and define the random residual variance. The name on the left-hand side of the | symbol names the log of the random residual variance. The name on the right-hand side of the | symbol specifies the name of the variable that has a random residual variance. Logv is the random residual variance for fw.

In the between part of the model, the BY statement specifies that fb is measured by the random intercepts y1, y2, y3, and y4. The metric of the factor is set automatically by the program by fixing the first factor loading to one. This option can be overridden. The intercepts and residual variances of the factor indicators are estimated and the residuals are not correlated as the default. The first ON statement describes the regression of fb on the cluster-level covariate w. The residual variance of the factor is estimated as the default. The intercept of the factor is fixed at zero as the default. The second ON statement describes the regression of the log of the random residual variance logv on the cluster-level covariate w. The intercept and residual variance of logv are estimated as the default. An explanation of the other commands can be found in Examples 9.1 and 9.28.

EXAMPLE 9.30: TWO-LEVEL TIME SERIES ANALYSIS WITH A UNIVARIATE FIRST-ORDER AUTOREGRESSIVE AR(1) MODEL FOR A CONTINUOUS DEPENDENT VARIABLE WITH A RANDOM INTERCEPT, RANDOM AR(1) SLOPE, AND RANDOM RESIDUAL VARIANCE

TITLE: this is an example of a two-level time series analysis with a univariate first-order autoregressive AR(1) model for a continuous dependent variable with a random intercept, random AR(1) slope, and random residual variance

DATA: FILE = ex9.30.dat;

VARIABLE: NAMES = z y w time subject;

BETWEEN = z w;

CLUSTER = subject;

LAGGED = y(1);

TINTERVAL = time (1);

ANALYSIS: TYPE = TWOLEVEL RANDOM;

ESTIMATOR = BAYES;

PROCESSORS = 2;

BITERATIONS = (2000);

MODEL: %WITHIN%

s | y ON y&1;

logv | y;

%BETWEEN%

y ON w;

s ON w;

logv ON w;

y s logv WITH y s logv;

z ON y s logv;

OUTPUT: TECH1 TECH8 FSCOMPARISON;

PLOT: TYPE = PLOT3;

FACTORS = ALL;

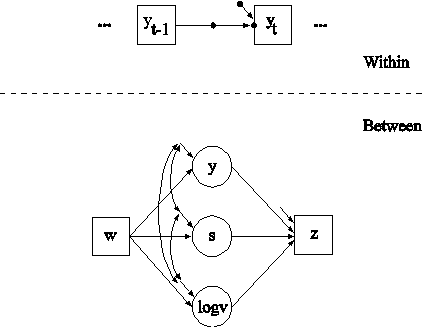
In this example, the two-level time series analysis with a univariate first-order autoregressive AR(1) model for a continuous dependent variable with a random intercept, random AR(1) slope, and random residual variance shown in the picture above is estimated (Asparouhov, Hamaker, & Muthén, 2017). The subscript t refers to a time point and the subscript t-1 refers to the previous time point. The dots indicate that the process includes both previous and future time points using the same model. In the within part of the model, the filled circle at the end of the arrow from y_t-1to y_t represents a random intercept that is referred to as y in the between part of the model. The filled circle on the arrow from y_t-1to y_t represents a random AR(1) slope that is referred to as s in the between part of the model. The filled circle at the end of the residual arrow pointing to y represents a random residual variance that is referred to as logv in the between part of the model. In the between part of the model, the random intercept, random AR(1) slope, and random residual variance are shown in circles because they are continuous latent variables that vary across clusters. In this model, the random intercept is the random mean because y in the within part of the model is centered. The log of the random residual variance is used in the model.

The LAGGED option of the VARIABLE command is used to specify the maximum lag to use for an observed variable during model estimation. The variable y has lag 1. The lagged variable is referred to by adding to the name of the variable an ampersand (&) and the number of the lag.

The TINTERVAL option is used in time series analysis to specify the time interval that is used to create a time variable when data are misaligned with respect to time due to missed measurement occasions that are not assigned a missing value flag and when measurement occasions are random. The data set must be sorted by the time interval variable. In this example, the time interval value is one and the time interval variable values are 1, 2, 3, etc.. This results in intervals of -.5 to 1.5, 1.5 to 2.5, and 2.5 to 3.5, etc.

In the between part of the model, the first ON statement describes the linear regression of the random intercept y on the observed cluster-level covariate w. The second ON statement describes the linear regression of the random AR(1) slope s on the observed cluster-level covariate w. The third ON statement describes the linear regression of the log of the random residual variance logv on the observed cluster-level covariate w. The intercepts and residual variances of y, s, and logv are estimated and the residuals are not correlated as the default. The WITH statement specifies that the residuals among y, s, and logv are correlated. The fourth ON statement describes the linear regression of the observed cluster-level dependent variable z on the random intercept y, the random AR(1) slope s, and the log of the random residual variance logv.

A two-level time series analysis with a univariate second-order autoregressive AR(2) model can also be estimated. For this analysis, the LAGGED option is specified as LAGGED = y (2); and the MODEL command is specified as follows:

MODEL: %WITHIN%

s1 | y ON y&1;

s2 | y ON y&2;

logv | y;

%BETWEEN%

y ON w;

s1-s2 ON w;

logv ON w;

y s1 s2 logv WITH y s1 s2 logv;

z ON y s1 s2 logv;

In the first | statement, the random AR(1) slope s1 is defined by the linear regression over multiple time points of the dependent variable y on the dependent variable y&1 which is y at the previous time point. In the second | statement, the random AR(2) slope s2 is defined by the linear regression over multiple time points of the dependent variable y on the dependent variable y&2 which is y at two time points prior. A model where only y at lag 2 is used is specified as follows:

MODEL: %WITHIN%

y ON y&1@0;

s2 | y ON y&2;

where the coefficient for y at lag 1 is fixed at zero.

In the OUTPUT command, the FSCOMPARISON option is used to request a comparison of between-level estimated factor scores. In the PLOT command, the FACTORS option is used with the keyword ALL to request that estimated factor scores for all between-level random effects be available for plotting. An explanation of the other commands can be found in Examples 9.1 and 9.28.

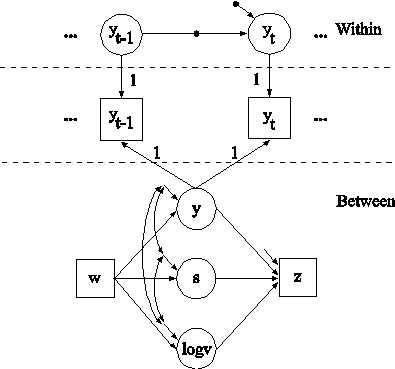
A more detailed picture of the model is shown above. This picture reflects that the dependent variable y is decomposed into two uncorrelated latent variables,

y_it = y_wit + y_bi,

where i represents individual, t represents time, y_wit is the latent variable used on the within level, and y_bi is the latent variable used on the between level. This model is described in Asparouhov, Hamaker, and Muthén (2017). The decomposition can also be expressed as

y_wit= y_it- y_bi,

which can be viewed as a latent group-mean centering of the within-level latent variable. For a further discussion of centering and latent variable decomposition, see Ludtke et al. (2008).

EXAMPLE 9.31: TWO-LEVEL TIME SERIES ANALYSIS WITH A UNIVARIATE FIRST-ORDER AUTOREGRESSIVE AR(1) MODEL FOR A CONTINUOUS DEPENDENT VARIABLE WITH A COVARIATE, RANDOM INTERCEPT, RANDOM AR(1) SLOPE, RANDOM SLOPE, AND RANDOM RESIDUAL VARIANCE

TITLE: this is an example of a two-level time

series analysis with a univariate first-order autoregressive AR(1) model for a continuous dependent variable with a covariate, random intercept, random AR(1) slope, random slope, and random residual variance

DATA: FILE = ex9.31.dat;

VARIABLE: NAMES = y x w xm subject;

WITHIN = x;

BETWEEN = w xm;

CLUSTER = subject;

LAGGED = y(1);

DEFINE: CENTER X (GROUPMEAN);

ANALYSIS: TYPE = TWOLEVEL RANDOM;

ESTIMATOR = BAYES;

PROCESSORS = 2;

BITERATIONS = (2000);

MODEL: %WITHIN%

sy | y ON y&1;

sx | y ON x;

logv | y;

%BETWEEN%

y ON w xm;

sy ON w xm;

sx ON w xm;

logv ON w xm;

y sy sx logv WITH y sy sx logv;

OUTPUT: TECH1 TECH8;

PLOT: TYPE= PLOT3;

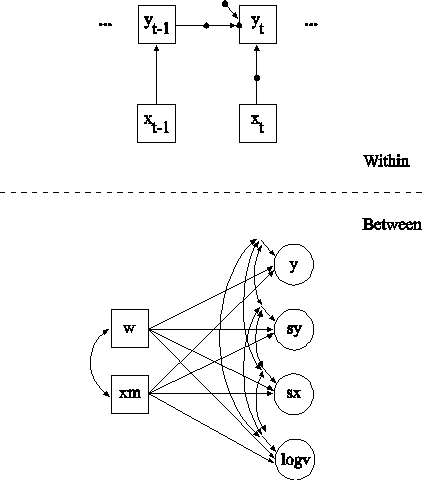
The difference between this example and Example 9.30 is that a covariate with a random slope is added and no cluster-level dependent variable is used. In this example, the two-level time series analysis with a univariate first-order autoregressive AR(1) model for a continuous dependent variable with a covariate, random intercept, random AR(1) slope, random slope, and random residual variance shown in the picture above is estimated. The log of the random residual variance is used in the model.

In the DEFINE command, the individual-level covariate x is centered using the cluster means for x. In this analysis, the cluster means are the means for each subject.

In the within part of the model, the | symbol is used in conjunction with TYPE=RANDOM to name and define the random variables in the model. The name on the left-hand side of the | symbol names the random variable. The statement on the right-hand side of the | symbol defines the random variable. In the first | statement, the random AR(1) slope sy is defined by the linear regression over multiple time points of the dependent variable y on the dependent variable y&1 which is y at the previous time point. In the second | statement, the random slope sx is defined by the linear regression over multiple time points of the dependent variable y on the observed individual-level covariate x. In the third | statement, the random residual variance logv is defined as the log of the residual variance of the dependent variable y.

In the between part of the model, the first ON statement describes the linear regression of the random intercept y on the observed cluster-level covariates w and xm. The second ON statement describes the linear regression of the random AR(1) slope sy on the observed cluster-level covariates w and xm. The third ON statement describes the linear regression of the random slope sx on the observed cluster-level covariates w and xm. The fourth ON statement describes the linear regression of the random residual variance logv on the observed cluster-level covariates w and xm. The intercepts and residual variances of y, sy, sx, and logv are estimated and the residuals are not correlated as the default. The WITH statement specifies that the residuals among y, sy, sx, and logv are correlated. An explanation of the other commands can be found in Examples 9.1, 9.28, and 9.30.

EXAMPLE 9.32: TWO-LEVEL TIME SERIES ANALYSIS WITH A BIVARIATE CROSS-LAGGED MODEL FOR CONTINUOUS DEPENDENT VARIABLES WITH RANDOM INTERCEPTS AND RANDOM SLOPES

TITLE: this is an example of a two-level time series analysis with a bivariate cross- lagged model for continuous dependent variables with random intercepts and random slopes

DATA: FILE = ex9.32.dat;

VARIABLE: NAMES = y1 y2 subject;

CLUSTER = subject;

LAGGED = y1(1) y2(1);

ANALYSIS: TYPE = TWOLEVEL RANDOM;

ESTIMATOR = BAYES;

PROCESSORS = 2;

BITERATIONS = (2000);

MODEL: %WITHIN%

s1 | y1 ON y1&1;

s2 | y2 ON y2&1;

s12 | y1 ON y2&1;

s21 | y2 ON y1&1;

%BETWEEN%

y1 y2 s1-s21 WITH y1 y2 s1-s21;

OUTPUT: TECH1 TECH8 STANDARDIZED (CLUSTER);

PLOT: TYPE = PLOT3;

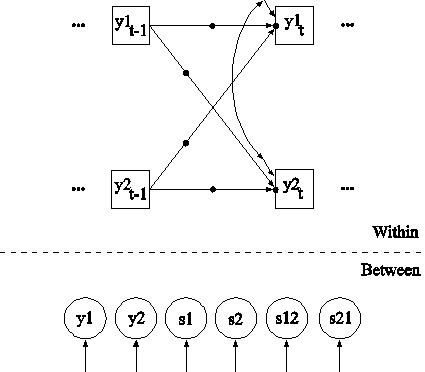
The difference between this example and Example 9.30 is that a bivariate cross-lagged model rather than a univariate first-order autoregressive AR(1) model is estimated. In this example, the two-level time series analysis with a bivariate cross-lagged model for continuous dependent variables with random intercepts and random slopes shown in the picture above is estimated.

In the within part of the model, the | symbol is used in conjunction with TYPE=RANDOM to name and define the random variables in the model. The name on the left-hand side of the | symbol names the random variable. The statement on the right-hand side of the | symbol defines the random variable. In the first | statement, the random AR(1) slope s1 is defined by the linear regression over multiple time points of the dependent variable y1 on the dependent variable y1&1 which is y1 at the previous time point. In the second | statement, the random AR(1) slope s2 is defined by the linear regression over multiple time points of the dependent variable y2 on the dependent variable y2&1 which is y2 at the previous time point. In the third | statement, the random cross-lagged slope s12 is defined by the linear regression over multiple time points of the dependent variable y1 on the dependent variable y2&1 which is y2 at the previous time point. In the fourth | statement, the random cross-lagged slope s21 is defined by the linear regression over multiple time points of the dependent variable y2 on the dependent variable y1&1 which is y1 at the previous time point.

In the between part of the model, the WITH statement specifies that y1, y2, s1, s2, s12, s21, are correlated.

In the OUTPUT command, the STANDARDIZED option is used to request standardized parameter estimates and their standard errors and R-square. When a model has random effects, each parameter is standardized for each cluster. The standardized values reported are the average of the standardized values across clusters for each parameter (Schuurman et al., 2016; Asparouhov, Hamaker, & Muthén, 2017). The CLUSTER setting requests that the standardized values for each cluster be printed in the output.

A two-level time series analysis with a bivariate cross-lagged model for continuous dependent variables with random residual variances and a random residual covariance can also be estimated. The MODEL command is specified as follows:

MODEL: %WITHIN%

s1 | y1 ON y1&1;

s2 | y2 ON y2&1;

s12 | y1 ON y2&1;

s21 | y2 ON y1&1;

logv1 | y1;

logv2 | y2;

f BY y1@1 y2@1;

logvf | f;

%BETWEEN%

y1 y2 s1-logvf WITH y1 y2 s1-logvf;

In the fifth | statement, the random residual variance logv1 is defined as the residual variance of the dependent variable y1. In the sixth | statement, the random residual variance logv2 is defined as the residual variance of the dependent variable y2. The logs of the random residual variances are used in the model. In the BY statement, the factor loadings for the factor f are fixed at one for the factor indicators y1 and y2. The variance of the factor f is the covariance between the residuals of y1 and y2. In the seventh | statement, the random residual covariance logvf is defined as the variance of the factor f. An explanation of the other commands can be found in Examples 9.1, 9.28, and 9.30.

EXAMPLE 9.33: TWO-LEVEL TIME SERIES ANALYSIS WITH A FIRST-ORDER AUTOREGRESSIVE AR(1) FACTOR ANALYSIS MODEL FOR A SINGLE CONTINUOUS INDICATOR AND MEASUREMENT ERROR

TITLE: this is an example of a two-level time series analysis with a first-order autoregressive AR(1) factor analysis model

for a single continuous indicator and measurement error

DATA: FILE = ex9.33.dat;

VARIABLE: NAMES = y subject;

CLUSTER = subject;

ANALYSIS: TYPE = TWOLEVEL RANDOM;

ESTIMATOR = BAYES;

PROCESSORS = 2;

BITERATIONS = (5000);

MODEL: %WITHIN%

f BY y@1(&1);

s | f ON f&1;

%BETWEEN%

y WITH s;

OUTPUT: TECH1 TECH8;

PLOT: TYPE = PLOT3;

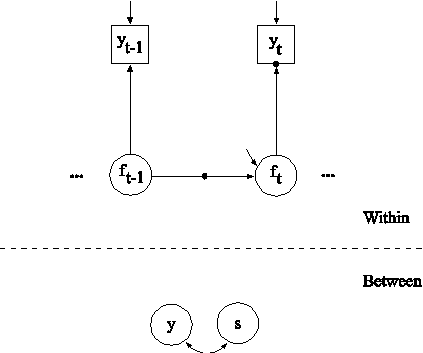
In this example, the two-level time series analysis with a first-order autoregressive AR(1) factor analysis model for a single continuous indicator and measurement error shown in the picture above is estimated.

The BITERATIONS option is used to specify the maximum and minimum number of iterations for each Markov chain Monte Carlo (MCMC) chain when the potential scale reduction (PSR) convergence criterion (Gelman & Rubin, 1992) is used. Using a number in parentheses, the BITERATIONS option specifies that a minimum of 5,000 and a maximum of the default of 50,000 iterations will be used. The minimum is relatively large because this model may be more difficult to estimate.

In the within part of the model, the BY statement specifies that the factor f is equivalent to the dependent variable y without measurement error. It is possible to identify measurement error because the model is autoregressive. An ampersand (&) followed by the number 1 is placed in parentheses following the BY statement to indicate that the factor f at lag 1 can be used in the analysis. The factor f at lag 1 is referred to as f&1. The | symbol is used in conjunction with TYPE=RANDOM to name and define the random variables in the model. The name on the left-hand side of the | symbol names the random variable. The statement on the right-hand side of the | symbol defines the random variable. In the | statement, the random AR(1) slope s is defined by the linear regression over multiple time points of the factor f on the factor f&1 which is f at the previous time point.

In the between part of the model, the WITH statement specifies that y and s are correlated.

A two-level time series analysis with an ARMA (1, 1) model where AR stands for autoregressive and MA stands for moving average (Shumway & Stoffer, 2011) shown in the picture below can also be estimated. As shown in Granger and Morris (1976) and Schuurman et al. (2015) for N=1 time series analysis, this is an alternative representation of the data used in the measurement error model shown above. For this analysis, the LAGGED option of the VARIABLE command is specified as LAGGED = y (1); and the MODEL command is specified as shown below.

MODEL: %WITHIN%

s | y ON y&1;

e BY y@1 (&1);

y@.01;

y ON e&1;

In the | statement, the random AR(1) slope s is defined by the linear regression over multiple time points of the dependent variable y on the dependent variable y&1 which is y at the previous time point. The BY statement together with fixing the residual variance of y at a small value specify that the factor e is equivalent to the residual of the dependent variable y. The small value of .01 is chosen rather than zero to obtain faster convergence. An ampersand (&) followed by the number 1 is placed in parentheses following the BY statement to indicate that the factor e at lag 1 can be used in the analysis. The factor e at lag 1 is referred to as e&1. The ON statement describes the linear regression of the dependent variable y on the residual e&1 which is the residual of y at the previous time point. This is the moving average component of the model. An explanation of the other commands can be found in Examples 9.1, 9.28, and 9.30.

EXAMPLE 9.34: TWO-LEVEL TIME SERIES ANALYSIS WITH A FIRST-ORDER AUTOREGRESSIVE AR(1) CONFIRMATORY FACTOR ANALYSIS (CFA) MODEL FOR CONTINUOUS FACTOR INDICATORS WITH RANDOM INTERCEPTS, A RANDOM AR(1) SLOPE, AND A RANDOM RESIDUAL VARIANCE

TITLE: this is an example of a two-level time series analysis with a first-order autoregressive AR(1) confirmatory factor analysis (CFA) model for continuous factor indicators with random intercepts, a random AR(1) slope, and a random residual variance

DATA: FILE = ex9.34.dat;

VARIABLE: NAMES = y1-y4 subject;

CLUSTER = subject;

ANALYSIS: TYPE = TWOLEVEL RANDOM;

ESTIMATOR = BAYES;

PROCESSORS = 2;

BITERATIONS = (2000);

MODEL: %WITHIN%

f BY y1-y4(&1);

s | f ON f&1;

logv | f;

%BETWEEN%

fb BY y1-y4*;

fb@1;

fb s logv WITH fb s logv;

OUTPUT: TECH1 TECH8;

PLOT: TYPE = PLOT3;

In this example, the two-level time series analysis with a first-order autoregressive AR(1) confirmatory factor analysis (CFA) model for continuous factor indicators with random intercepts, a random AR(1) slope, and a random residual variance shown in the picture above is estimated. The log of the random residual variance is used in the model.

In the within part of the model, the BY statement specifies that f is measured by y1, y2, y3, and y4. The metric of the factor is set automatically by the program by fixing the first factor loading to one. This option can be overridden. An ampersand (&) followed by the number 1 is placed in parentheses following the BY statement to indicate that the factor f at lag 1 can be used in the analysis. The factor f at lag 1 is referred to as f&1. The residual variances of the factor indicators are estimated and the residuals are not correlated as the default. The | symbol is used in conjunction with TYPE=RANDOM to name and define the random variables in the model. The name on the left-hand side of the | symbol names the random variable. The statement on the right-hand side of the | symbol defines the random variable. In the first | statement, the random AR(1) slope s is defined by the linear regression over multiple time points of the factor f on the factor f&1 which is f at the previous time point. In the second | statement, the random residual variance logv is defined as the log of the residual variance of the factor f.

In the between part of the model, the BY statement specifies that fb is measured by the random intercepts y1, y2, y3, and y4. The metric of the factor is set automatically by the program by fixing the first factor loading to one. The asterisk following y1-y4 overrides this default. The metric of the factor is set by fixing the factor variance to one. The WITH statement specifies that fb, s, and logv are correlated. An explanation of the other commands can be found in Examples 9.1, 9.28, and 9.30.

EXAMPLE 9.35: TWO-LEVEL TIME SERIES ANALYSIS WITH A FIRST-ORDER AUTOREGRESSIVE AR(1) IRT MODEL FOR BINARY FACTOR INDICATORS WITH RANDOM THRESHOLDS, A RANDOM AR(1) SLOPE, AND A RANDOM RESIDUAL VARIANCE

TITLE: this is an example of a two-level time series analysis with a first-order autoregressive AR(1) IRT model for binary factor indicators with random thresholds, a random AR(1) slope, and a random residual variance

DATA: FILE = ex9.35part2.dat;

VARIABLE: NAMES = u1-u4 subject;

CATEGORICAL = u1-u4;

CLUSTER = subject;

ANALYSIS: TYPE = TWOLEVEL RANDOM;

ESTIMATOR = BAYES;

PROCESSORS = 2;

BITERATIONS = (3000);

MODEL: %WITHIN%

f BY u1-u4*(&1 1-4);

s | f ON f&1;

logvf | f;

%BETWEEN%

fb BY u1-u4* (1-4);

[logvf@0];

fb s logvf WITH fb s logvf;

OUTPUT: TECH1 TECH8;

In this example, a two-level time series analysis with a first-order autoregressive AR(1) IRT model for binary factor indicators with random thresholds, a random AR(1) slope, and a random residual variance is estimated. The log of the random residual variance is used in the model.

The CATEGORICAL option specifies that the variables u1, u2, u3, and u4 are binary. The BITERATIONS option is used to specify the maximum and minimum number of iterations for each Markov chain Monte Carlo (MCMC) chain when the potential scale reduction (PSR) convergence criterion (Gelman & Rubin, 1992) is used. Using a number in parentheses, the BITERATIONS option specifies that a minimum of 3,000 and a maximum of the default of 50,000 iterations will be used. The minimum is relatively large because this model may be more difficult to estimate

In the within part of the model, the BY statement specifies that f is measured by u1, u2, u3, and u4. The metric of the factor is set automatically by the program by fixing the first factor loading to one. The asterisk following u1-u4 overrides this default. The metric of the factor is set by fixing the mean of the log of the random residual variance of the factor f to zero in the between part of the model which is described below. An ampersand (&) followed by the number 1 is placed in parentheses following the BY statement to indicate that the factor f at lag 1 can be used in the analysis. The factor f at lag 1 is referred to as f&1. The numbers 1-4 in parentheses in combination with the same numbers in the between part of the model specify that the factor loadings are constrained to be equal to those of the factor fb in the between part of the model. The | symbol is used in conjunction with TYPE=RANDOM to name and define the random variables in the model. The name on the left-hand side of the | symbol names the random variable. The statement on the right-hand side of the | symbol defines the random variable. In the first | statement, the random AR(1) slope s is defined by the linear regression over multiple time points of the factor f on the factor f&1 which is f at the previous time point. In the second | statement, the random residual variance logvf is defined as the log of the residual variance of the factor f.

In the between part of the model, the BY statement specifies that fb is measured by the random intercepts u1, u2, u3, and u4. The metric of the factor is set automatically by the program by fixing the first factor loading to one. The asterisk following u1-u4 overrides this default. Because the factor loadings are constrained to be equal for the within-level factor f and the between-level factor fb, the metric of the factors can be set by fixing the mean of the log of the random residual variance of the factor f to zero or the variance of the factor fb to one. The WITH statement specifies that fb, s, and logvf are correlated. An explanation of the other commands can be found in Examples 9.1, 9.28, and 9.30.

EXAMPLE 9.36: TWO-LEVEL TIME SERIES ANALYSIS WITH A BIVARIATE CROSS-LAGGED MODEL FOR TWO FACTORS AND CONTINUOUS FACTOR INDICATORS WITH RANDOM INTERCEPTS AND RANDOM SLOPES

TITLE: two-level time series analysis with a bivariate cross-lagged model for two factors and continuous factor indicators with random intercepts and random slopes

DATA: FILE = ex9.36.dat;

VARIABLE: NAMES = y11-y14 y21-y24 subject;

CLUSTER = subject;

ANALYSIS: TYPE = TWOLEVEL RANDOM;

ESTIMATOR = BAYES;

PROCESSORS = 2;

BITERATIONS = (2000);

MODEL: %WITHIN%

f1 BY y11-y14(&1);

f2 BY y21-y24(&1);

s11 | f1 ON f1&1;

s22 | f2 ON f2&1;

s12 | f1 ON f2&1;

s21 | f2 ON f1&1;

%BETWEEN%

fb1 BY y11-y14*;

fb2 BY y21-y24*;

fb1-fb2@1;

fb1 fb2 s11-s21 WITH fb1 fb2 s11-s21;

OUTPUT: TECH1 TECH8;

PLOT: TYPE = PLOT3;

In this example, the two-level time series analysis with a bivariate cross-lagged model for two factors and continuous factor indicators with random intercepts and random slopes shown in the picture above is estimated.

In the within part of the model, the first BY statement specifies that f1 is measured by y11, y12, y13, and y14. The second BY statement specifies that f2 is measured by y21, y22, y23, and y24. The metric of the factors is set automatically by the program by fixing the first factor loading to one. This option can be overridden. An ampersand (&) followed by the number 1 is placed in parentheses following the BY statements to indicate that the factors f1 and f2 at lag 1 are used during model estimation. The factors f1 and f2 at lag 1 are referred to as f1&1 and f2&1, respectively. The residual variances of the factor indicators are estimated and the residuals are not correlated as the default. The | symbol is used in conjunction with TYPE=RANDOM to name and define the random variables in the model. The name on the left-hand side of the | symbol names the random variable. The statement on the right-hand side of the | symbol defines the random variable. In the first | statement, the random AR(1) slope s11 is defined by the linear regression over multiple time points of the factor f1 on the factor f1&1 which is f1 at the previous time point. In the second | statement, the random AR(1) slope s22 is defined by the linear regression over multiple time points of the factor f2 on the factor f2&1 which is f2 at the previous time point. In the third | statement, the random cross-lagged slope s12 is defined by the linear regression over multiple time points of the factor f1 on the factor f2&1 which is f2 at the previous time point. In the fourth | statement, the random cross-lagged slope s21 is defined by the linear regression over multiple time points of the factor f2 on the factor f1&1 which is f1 at the previous time point.

In the between part of the model, the first BY statement specifies that f1 is measured by the random intercepts y11, y12, y13, and y14. The second BY statement specifies that f2 is measured by the random intercepts y21, y22, y23, and y24. The metric of the factors is set automatically by the program by fixing the first factor loadings to one. The asterisk following y11-y14 and y21-y24 overrides this default. The metric of the factors is set by fixing the factor variances to one. The WITH statement specifies that fb1, fb2, s11, s22, s12, and s21 are correlated. An explanation of the other commands can be found in Examples 9.1, 9.28, and 9.30.

EXAMPLE 9.37: TWO-LEVEL TIME SERIES ANALYSIS WITH A UNIVARIATE FIRST-ORDER AUTOREGRESSIVE AR(1) MODEL FOR A CONTINUOUS DEPENDENT VARIABLE WITH A COVARIATE, LINEAR TREND, RANDOM SLOPES, AND A RANDOM RESIDUAL VARIANCE

TITLE: two-level time series analysis with a univariate first-order autoregressive AR(1) model for a continuous dependent variable with a covariate, linear trend, random slopes, and a random residual variance

DATA: FILE = ex9.37.dat;

VARIABLE: NAMES = y x w xm time subject;

WITHIN = x time;

BETWEEN = w xm;

CLUSTER = subject;

LAGGED = y(1);

DEFINE: CENTER x (GROUPMEAN);

ANALYSIS: TYPE = TWOLEVEL RANDOM;

ESTIMATOR = BAYES;

PROCESSORS = 2;

BITERATIONS = (10000);

MODEL: %WITHIN%

sy | y ON y&1;

sx | y ON x;

s | y ON time;

logv | y;

%BETWEEN%

sy ON w xm;

sx ON w xm;

s ON w xm;

logv ON w xm;

y ON w xm;

sy-logv y WITH sy-logv y;

OUTPUT: TECH1 TECH8;

PLOT: TYPE= PLOT3;

In this example, the two-level time series analysis with a univariate first-order autoregressive AR(1) model for a continuous dependent variable with a covariate, linear trend, random slopes, and a random residual variance shown in the picture above is estimated. The log of the random residual variance is used in the model.

In the within part of the model, the | symbol is used in conjunction with TYPE=RANDOM to name and define the random variables in the model. The name on the left-hand side of the | symbol names the random variable. The statement on the right-hand side of the | symbol defines the random variable. In the first | statement, the random AR(1) slope sy is defined by the linear regression over multiple time points of the dependent variable y on the dependent variable y&1 which is y at the previous time point. In the second | statement, the random slope sx is defined by the linear regression over multiple time points of the dependent variable y on the observed individual-level covariate x. In the third | statement, the random linear trend s is defined by the linear regression over multiple time points of the dependent variable y on the observed individual-level covariate time. In the fourth | statement, the random residual variance logv is defined as the log of the residual variance of the dependent variable y.

In the between part of the model, the first ON describes the linear regression of the random AR(1) slope sy on the observed cluster-level covariates w and xm. The second ON statement describes the linear regression of the random slope sx on the observed cluster-level covariates w and xm. The third ON statement describes the linear regression of the random linear trend s on the observed cluster-level covariates w and xm. The fourth ON statement describes the linear regression of the random residual variance logv on the observed cluster-level covariates w and xm. The fifth ON statement describes the linear regression of the random intercept y on the observed cluster-level covariates w and xm. The intercepts and residual variances of sy, sx, s, logv, and y are estimated and the residuals are not correlated as the default. The WITH statement specifies that the residuals among sy, sx, s, logv, and y are correlated. An explanation of the other commands can be found in Examples 9.1, 9.28, 9.30, and 9.31.

EXAMPLE 9.38: CROSS-CLASSIFIED TIME SERIES ANALYSIS WITH A UNIVARIATE FIRST-ORDER AUTOREGRESSIVE AR(1) MODEL FOR A CONTINUOUS DEPENDENT VARIABLE WITH A COVARIATE, RANDOM INTERCEPT, AND RANDOM SLOPE

TITLE: cross-classified time series analysis with a univariate first-order autoregressive AR(1) model for a continuous dependent variable with a covariate, random intercept, and random slope

DATA: FILE = ex9.38.dat;

VARIABLE: NAMES = w xm y x time subject;

CLUSTER = subject time;

WITHIN = x;

BETWEEN = (subject)w xm;

LAGGED = y(1);

DEFINE: CENTER x (GROUPMEAN subject);

ANALYSIS: TYPE = CROSSCLASSIFIED RANDOM;

ESTIMATOR = BAYES;

PROCESSORS = 2;

BITERATIONS = (2000);

MODEL: %WITHIN%

sx | y ON x;

y ON y&1;

%BETWEEN subject%

y sx ON w xm;

y WITH sx;

%BETWEEN time%

y WITH sx;

OUTPUT: TECH1 TECH8;

PLOT: TYPE = PLOT3;

FACTORS = ALL;

In this example, the cross-classified time series analysis with a univariate first-order autoregressive AR(1) model for a continuous dependent variable with a covariate, random intercept, and random slope shown in the picture above is estimated.

The CLUSTER option is used to identify the variables in the data set that contain clustering information. Two cluster variables are used for a cross-classified time series model. One is for subject and the other for time. Subject and time are crossed. There is no nesting because each subject is observed only once at any one time. The cluster variable for subject must precede the cluster variable for time. Within each cluster, data must be ordered by time.

The WITHIN option is used to identify the variables in the data set that are measured on the individual level and to specify the levels on which they are modeled. All variables on the WITHIN list must be measured on the individual level. An individual-level variable can be modeled on all or some levels. If a variable measured on the individual level is mentioned on the WITHIN list without a label, it is modeled only in the within part of the model. It has no variance in the between subject and between time parts of the model. If a variable is not mentioned on the WITHIN list, it is modeled on all levels. The variable x can be modeled in only the within part of the model.

The BETWEEN option is used to identify the variables in the data set that are measured on the cluster level(s) and to specify the level(s) on which they are modeled. All variables on the BETWEEN list must be measured on a cluster level. For TYPE=CROSSCLASSIFIED, a variable measured on the subject level must be mentioned on the BETWEEN list with a subject label. It can be modeled in only the between subject part of the model. A variable measured on the time level must be mentioned on the BETWEEN list with a time label. It can be modeled in only the between time part of the model. The variables w and xm can be modeled in only the between subject part of the model.

In the ANALYSIS command, TYPE=CROSSCLASSIFIED RANDOM is specified indicating that a cross-classified model will be estimated. In the within part of the model, the | symbol is used in conjunction with TYPE=RANDOM to name and define the random variables in the model. The name on the left-hand side of the | symbol names the random variable. The statement on the right-hand side of the | symbol defines the random variable. In the | statement, the random slope sx is defined by the linear regression over multiple time points of the dependent variable y on the observed individual-level covariate x. The ON statement describes the linear regression over multiple time points of the dependent variable y on the dependent variable y&1 which is y at the previous time point.

In the between subject part of the model, the ON statement describes the linear regressions of the random intercept y and the random slope sx on the observed cluster-level covariates w and xm. The intercepts and residual variances of y and sx across subjects are estimated and the residuals are not correlated as the default. The WITH statement specifies that the residuals among y and sx are correlated. In the between time part of the model, the WITH statement specifies that y and sx are correlated. The variances of y and sx across time are estimated as the default.

A cross-classified time series analysis with a univariate first-order autoregressive AR(1) model for a continuous dependent variable with a random AR(1) slope and a random residual variance can also be estimated. The estimation of this model is computationally demanding. The MODEL command is specified as follows:

MODEL: %WITHIN%

sx | y ON x;

sy | y ON y&1;

logv | y;

%BETWEEN subject%

y sx sy logv ON w xm;

y sx-logv WITH y sx-logv;

%BETWEEN time%

y sx-sy WITH y sx-sy;

In the second | statement, the random AR(1) slope sy is defined by the linear regression over multiple time points of the dependent variable y on the dependent variable y&1 which is y at the previous time point. In the third | statement, the random residual variance logv is defined as the log of the residual variance of the dependent variable y. The log of the random residual variance is used in the model.

In the between subject part of the model, the ON statement describes the linear regression of the random intercept y, the random slope sx, the random AR(1) slope sy, and the random residual variance logv on the observed cluster-level covariates w and xm. The intercepts and residual variances of y, sx, sy, and logv across subjects are estimated and the residuals are not correlated as the default. The WITH statement specifies that the residuals among y, sx, sy, and logv are correlated.

In the between time part of the model, the variances of y, sx, and sy across subjects are estimated and they are not correlated as the default. The WITH statement specifies that y, sx, and sy are correlated. An explanation of the other commands can be found in Examples 9.1, 9.28, 9.30, and 9.31.

EXAMPLE 9.39: CROSS-CLASSIFIED TIME SERIES ANALYSIS WITH A UNIVARIATE FIRST-ORDER AUTOREGRESSIVE AR(1) MODEL FOR A CONTINUOUS DEPENDENT VARIABLE WITH A COVARIATE, LINEAR TREND, AND RANDOM SLOPE

TITLE: this is an example of a cross-classified time series analysis with a univariate first-order autoregressive AR(1) model for a continuous dependent variable with a covariate, linear trend, and random slope

DATA: FILE = ex9.39.dat;

VARIABLE: NAMES = w xm y x time subject;

USEVARIABLES = w xm y x timew timet;

WITHIN = x timew;

BETWEEN = (subject) w xm (time) timet;

CLUSTER = subject time;

LAGGED = y(1);

DEFINE: timew = time;

timet = time;

CENTER x (GROUPMEAN subject);

ANALYSIS: TYPE = CROSSCLASSIFIED RANDOM;

ESTIMATOR = BAYES;

PROCESSORS = 2;

BITERATIONS = (5000);

MODEL: %WITHIN%

y ON y&1;

s | y ON timew;

sx | y ON x;

%BETWEEN subject%

y s sx ON w xm;

y s sx WITH y s sx;

%BETWEEN time%

sx ON timet;

y WITH sx;

s@0;

OUTPUT: TECH1 TECH8;

PLOT: TYPE = PLOT3;

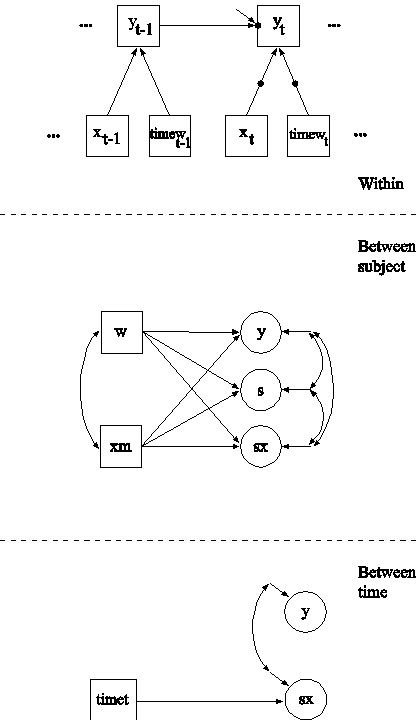
In this example, the cross-classified time series analysis with a univariate first-order autoregressive AR(1) model for a continuous dependent variable with a covariate, linear trend, and random slope shown in the picture above is estimated.

In the DEFINE command, the variables timew and timet are created as duplicates of the cluster variable time. Timew is used in the within part of the model and timet is used in the between time part of the model. The variables timew and timet are placed at the end of the USEVARIABLES list after the original variables to indicate that they will be used in the analysis. The individual-level covariate x is centered using the cluster means for x.

The BITERATIONS option is used to specify the maximum and minimum number of iterations for each Markov chain Monte Carlo (MCMC) chain when the potential scale reduction (PSR) convergence criterion (Gelman & Rubin, 1992) is used. Using a number in parentheses, the BITERATIONS option specifies that a minimum of 5,000 and a maximum of the default of 50,000 iterations will be used. The minimum is relatively large because this model may be more difficult to estimate.

In the within part of the model, the ON statement describes the linear regression over multiple time points of the dependent variable y on the dependent variable y&1 which is y at the previous time point. The | symbol is used in conjunction with TYPE=RANDOM to name and define the random variables in the model. The name on the left-hand side of the | symbol names the random variable. The statement on the right-hand side of the | symbol defines the random variable. In the first | statement, the random linear trend s is defined by the linear regression over multiple time points of the dependent variable y on the observed individual-level covariate timew. In the second | statement, the random slope sx is defined by the linear regression over multiple time points of the dependent variable y on the observed individual-level covariate x.

In the between subject part of the model, the ON statement describes the linear regression of the random intercept y, the random linear trend s, and the random slope sx on the observed subject-level covariates w and xm. The WITH statement specifies that the residuals among y, s, and sx are correlated.

In the between time part of the model, the ON statement describes the linear regression of the random slope sx on the observed time-level covariate timet. The WITH statement specifies that the residuals among y and sx are correlated. The variance of the random linear trend s is free as the default but is fixed at zero because it can be difficult to estimate and is not a necessary model component.

A cross-classified time series analysis with a univariate first-order autoregressive AR(1) model for a continuous dependent variable with a random AR(1) slope and a random residual variance can also be estimated. The estimation of this model is very demanding computationally. The MODEL command is specified as follows:

MODEL: %WITHIN%

sy | y ON y&1;

s | y ON timew;

sx | y ON x;

logv | y;

%BETWEEN subject%

y sy sx logv s ON w xm;

y sy sx logv s WITH y sy s logv s;

%BETWEEN time%

sx ON timet;

y sy sx WITH y sy sx;

s@0;

In the first | statement, the random AR(1) slope sy is defined by the linear regression over multiple time points of the dependent variable y on the dependent variable y&1 which is y at the previous time point. In the fourth | statement, the random residual variance logv is defined as the log of the residual variance of the dependent variable y. The log of the random residual variance is used in the model. The random AR(1) slope sy is allowed to vary across both subjects and time whereas the random residual variance logv is allowed to vary only across subjects. An explanation of the other commands can be found in Examples 9.1, 9.28, 9.30, and 9.38.

EXAMPLE 9.40: CROSS-CLASSIFIED TIME SERIES ANALYSIS WITH A UNIVARIATE FIRST-ORDER AUTOREGRESSIVE AR(1) CONFIRMATORY FACTOR ANALYSIS (CFA) MODEL FOR CONTINUOUS FACTOR INDICATORS WITH RANDOM INTERCEPTS AND A FACTOR VARYING ACROSS BOTH SUBJECTS AND TIME

TITLE: this is an example of a cross-classified time series analysis with a first-order autoregressive AR(1) confirmatory factor analysis (CFA) model for continuous factor indicators with random intercepts and a factor varying across both subjects and time

DATA: FILE = ex9.40.dat;

VARIABLE: NAMES = y1-y3 time subject;

CLUSTER = subject time;

ANALYSIS: TYPE = CROSSCLASSIFIED RANDOM;

ESTIMATOR = BAYES;

PROCESSORS = 2;

BITERATIONS = (1000);

MODEL: %WITHIN%

f BY y1-y3* (&1 1-3);

f@1;

f ON f&1;

%BETWEEN subject%

fsubj BY y1-y3* (1-3);

%BETWEEN time%

ftime BY y1-y3* (1-3);

OUTPUT: TECH1 TECH8;

PLOT: TYPE = PLOT3;

FACTORS = ALL;

In this example, the cross-classified time series analysis with a first-order autoregressive AR(1) confirmatory factor analysis (CFA) model for continuous factor indicators with random intercepts and a factor varying across both subjects and time shown in the picture above is estimated.

In the within part of the model, the BY statement specifies that f is measured by y1, y2, and y3. The metric of the factor is set automatically by the program by fixing the first factor loading to one. The asterisk following y1-y3 overrides this default. The metric of the factor is set by fixing the factor residual variance to one. An ampersand (&) followed by the number 1 is placed in parentheses following the BY statement to indicate that the factor f at lag 1 can be used in the analysis. The factor f at lag 1 is referred to as f&1. The numbers 1-3 in parentheses in combination with the same numbers in the between subject and between time parts of the model specify that the factor loadings are constrained to be equal to those of the factor fsubj in the between subject part of the model and the factor ftime in the between time part of the model. The ON statement describes the linear regression over multiple time points of the factor f on the factor f&1 which is f at the previous time point.

In the between subject part of the model, the intercepts and residual variances of the random intercepts of the within-level factor indicators are estimated and the residuals are not correlated as the default. In the between time part of the model, the residual variances of the random intercepts of the within-level factor indicators are estimated and the residuals are not correlated as the default.

In the second part of this example, a cross-classified time series analysis with a first-order autoregressive AR(1) confirmatory factor analysis (CFA) model for continuous factor indicators with random intercepts, random factor loadings, and a factor varying across both subjects and time is estimated.

TITLE: this is an example of a cross-classified time series analysis with a first-order autoregressive AR(1) confirmatory factor analysis (CFA) model for continuous factor indicators with random intercepts, random factor loadings, and a factor varying across both subjects and time

DATA: FILE = ex9.40part2.dat;

VARIABLE: NAMES = y1-y3 time subject;

CLUSTER = subject time;

ANALYSIS: TYPE = CROSSCLASSIFIED RANDOM;

ESTIMATOR = BAYES;

PROCESSORS = 2;

BITERATIONS = (1000);

MODEL: %WITHIN%

s1-s3 | f BY y1-y3 (&1);

f@1;

f ON f&1;

%BETWEEN subject%

%BETWEEN time%

OUTPUT: TECH1 TECH8;

PLOT: TYPE = PLOT3;

In the within part of the model, the | symbol is used in conjunction with TYPE=RANDOM to name and define the random variables in the model. The name on the left-hand side of the | symbol names the random variable. The statement on the right-hand side of the | symbol defines the random variable. In the | statement, the random factor loadings s1, s2, and s3 are defined by the linear regression over multiple time points of the factor indicators y1, y2, and y3 on the factor f. The variance of the factor is fixed at one to set the metric of the factor. An ampersand (&) followed by the number 1 is placed in parentheses following the BY statement to indicate that the factor f at lag 1 can be used in the analysis. The factor f at lag 1 is referred to as f&1. The intercepts of the factor indicators are random. The residual variances are estimated and the residuals are not correlated as the default. The ON statement describes the linear regression of the factor f on the factor f&1 which is f at the previous time point.

In the between subject and between time parts of the model, the factor f does not need to be defined using a BY statement because the factor loadings are random. In the between subject part of the model, the random intercepts and random factor loadings of the within-level factor indicators and the factor f vary across subjects. The means and variances of the random intercepts and random factor loadings are estimated and not correlated as the default. The factor variance is estimated only when mentioned. In the between time part of the model, the random intercepts of the within-level factor indicators and the factor f vary across time. The variances of the random intercepts are estimated and not correlated as the default. The factor variance is estimated only when mentioned. An explanation of the other commands can be found in Examples 9.1, 9.28, 9.30, and 9.38.